Динамические расчеты воздействия высокоскоростных поездов на грунты земляного полотна

Об актуальности проблемы

Изучение вопроса о проектировании железнодорожных магистралей, по которым могли бы двигаться поезда со скоростью 160–200 км/ч, началось в СССР еще в конце 1960-х – в 1970-х годах. Работа над первым проектом обеспечения скорости движения до 300–350 км/ч началась в 1987–1990 годах. В 1991 году президент РСФСР Борис Ельцин подписал указ «О создании высокоскоростной пассажирской железнодорожной магистрали (ВСМ) Санкт-Петербург – Москва». В 1995 году проект был принят, но в 1998-м Ельцин отменил свой указ 1991 года, и работы по реализации проекта так и не были начаты.

В итоге вместо создания отдельной железнодорожной магистрали в 1996–2003 годах реконструировали существующую и запустили между Москвой и Санкт-Петербургом поезда «Сапсан» немецкого производства, имеющие в этих условиях скорость 170 км/ч. Но при всех преимуществах это отрицательно сказалось на движении пригородных поездов и на грузовых перевозках из-за нехватки пропускной способности железной дороги.

В 2006 году опять заговорили о строительстве новой ВСМ. В 2011 году даже был презентован новый проект ВСМ Санкт-Петербург – Москва, но в 2013 году его снова отложили, отдав предпочтение направлению Москва – Нижний Новгород – Казань с перспективой продления до Екатеринбурга.

И все же 10 апреля 2019 года президент РФ Владимир Путин вновь одобрил приоритетность проектирования и строительства ВСМ Санкт-Петербург – Москва в ответ на просьбу генерального директора ОАО «РЖД» Олега Белозерова и врио губернатора Петербурга Александра Беглова (впрочем, в перспективе все равно предполагается трассы из Москвы в Санкт-Петербург и в Казань объединить в ВСМ «Евразия», которая свяжет Китай и Европу).

Предварительная оценка стоимости строительства ВСМ между Москвой и Петербургом составила 1,5 трлн рублей. При этом предполагалось, что социально-экономические выгоды от эксплуатации магистрали в конце концов более чем в 2 раза превысят затраты, необходимые на реализацию проекта. Но до сих пор нет решения о точном выборе новой трассы с закупкой поездов Alstom во Франции со скоростью движения до 300–350 км/ч или о комплексной реконструкции старой трассы для увеличения средней скорости имеющихся «Сапсанов» с нынешних 170 до 250–280 км/ч. Также много споров и о методах строительства или реконструкции, которые для высокоскоростных (200–400 км/ч), поездов должны быть не такими, как для обычных железнодорожных составов.

Все-таки магистраль между Москвой и Санкт-Петербургом была построена еще в середине XIX века и была рассчитана на другие скорости и нагрузки. Реконструкция путей с запуском поездов «Сапсан» стала большим шагом вперед, но это приблизило трассу к пределу возможностей. Чтобы увеличить скорость и пропускную способность, надо менять конструкцию земляного полотна и верхнего строения пути. Однако опыт организации высокоскоростного движения в зарубежных странах говорит о том, что предельные скорости достигаются на новых линиях. Скорее всего, было бы слишком дорого или даже невозможно приспособить дорогу, построенную в 1851 году, под высокоскоростное движение. Необходимо устройство верхнего строения пути на щебеночном балласте и правильно выбранных защитных слоях, бесстыкового пути на железобетонных шпалах или плитном основании, использование демпфирующих матов вблизи жилых массивов. Нужны точные расчеты крутизны откосов, ширины земляного полотна и междупутного расстояния на разных участках пути, минимального интервала между высокоскоростными поездами на перегонах, максимальных допустимых нагрузок на оси колесных пар. Необходимо определить необходимость использования эстакад или тоннелей на определенных участках, идеально выполнить водоотведение, полностью исключить возможность морозного пучения и неравномерных осадок грунтов под трассой и т.д. [1–9].

В любом случае развитие высокоскоростного железнодорожного движения в России сейчас стало особенно актуальным. Интерес геотехников, строителей, руководителей всех рангов и общественности к данной проблеме вновь резко повысился. В связи с этим предлагаем вниманию читателей обзор материалов статьи «3D-моделирование нагрузок на насыпь от движущихся поездов» [10], написанной М. Шахраки, М. Р. С. Садагиани и К. Й. Виттом из Университета «Баухаус» (Веймар, Германия), а также Т. Мейером из немецкой компании Baugrund Dresden Ingenieurgesellschaft mbH (Дрезден, Германия) и опубликованной в журнале Plaxis Bulletin в 2014 году. Предложенный подход к моделированию и приведенные примеры, возможно, будут полезными для тех, кто занимается проектированием железнодорожных магистралей, в том числе высокоскоростных.

Подход к моделированию нагрузок на насыпь от движущихся поездов, предложенный М. Шахраки с соавторами

М. Шахраки с соавторами [10] подчеркивают, что увеличение интенсивности и скорости движения поездов на современных железных дорогах требует комплексного анализа с акцентом на динамическом поведении грунта. Для получения реалистичных результатов большое значение имеет надлежащее моделирование динамического поведения системы «верхнее строение пути – грунт насыпи – естественное основание» при воздействиях от движущегося поезда.

С точки зрения динамики сооружений, как поясняют авторы работы [10], подвижная нагрузка меняет свое место во времени и по сравнению со статической нагрузкой может значительно увеличить деформации в конструкциях. Кроме того, она приводит к другому поведению грунта, которое до сих пор не было полностью изучено. Динамические деформации, вызываемые поездами, обычно не являются упругими. А совокупная пластическая деформация в течение срока службы железнодорожного пути постепенно увеличивается, причем ее величина зависит от нескольких факторов, в том числе от параметров материалов насыпи и грунтов основания.

Например, обычными являются неровности пути, которые появляются из-за пространственных изменений грунтов насыпи и ее основания (неравномерные осадки). При этом с увеличением скорости движения поездов влияние неровностей повышается. Это необходимо учитывать при моделировании системы «верхнее строение пути – грунт насыпи – естественное основание» путем уменьшения допустимой погрешности модели.

Далее Шахраки с соавторами [10] указывают на еще одну важную проблему, которая требует решения. Дело в том, что после достижения критической скорости поезда в динамическом отклике вышеуказанной системы появляется большое динамическое усиление – и проведение моделирования здесь очень важно для определения этой критической скорости. В связи с этим в статье [10] приводятся примеры численного моделирования, выполненного другими исследователями ранее. Так, Вогель с соавторами (Vogel et al., 2011) провели исследование динамической устойчивости железнодорожных путей на слабых грунтах, смоделировав железнодорожную насыпь в программе PLAXIS 2D и сопоставив полученные численные результаты с экспериментальными данными. Корейа с коллегами (Correia et al., 2007) также выполнили предварительное исследование сравнительной пригодности 2D-моделирования для решения указанной проблемы с помощью PLAXIS 2D и других конечноэлементных программ. В недавних (на момент написания статьи [10] в 2014 году) исследованиях с помощью некоторых допущений в какой-то мере учитывалось влияние третьего измерения. Например, Ян и Хун (Yang, Hung, 2001) предложили так называемую 2,5-мерную модель для подвижных нагрузок.

Достоверность модели, как подчеркивают Шахраки и др. [10], во многом зависит от ее точности, исходных данных и выбора подходящей теории, лежащей в ее основе. Представленные ими результаты были основаны на трехмерном моделировании и явились первым вкладом в создание метода моделирования подвижных нагрузок.

Они поясняют, что реакции, вызванные подвижными нагрузками на железнодорожный путь, существенно различаются в зависимости от нагруженности и скорости поездов. Во время движения колеса воздействие происходит не только на точку контакта, но и на соседние области.

Для оценки сил сдвига в рельсе авторами статьи [10] сначала был выполнен статический анализ, основанный на теории «балки на упругом основании», с помощью расчетов в программе PROKON. Эта программа выполняет линейный анализ, в котором балка моделируется как двумерная конструкция на серии пружин с очень короткими расстояниями между ними. Статический анализ был нужен, чтобы аппроксимировать длину распределения сдвиговых сил в рельсе, необходимую для последующего учета при увеличении длины модели. Силы сдвига, полученные с помощью этого анализа, затем использовались в конечноэлементной программе PLAXIS 3D в качестве динамических множителей (то есть динамических коэффициентов определяющих амплитуду воздействия заданной силы или перемещения) для каждой точечной нагрузки.

Шахраки с соавторами [10] приняли, что расстояние между двумя опорами под балкой довольно мало и она опирается непосредственно на грунт (рис. 1).

Рис. 1. Теория и допущения [10]

Длина поезда L определяет длину модели. Кроме того, эта длина была увеличена авторами работы [10] на 0,18L с обеих сторон рельса, чтобы учесть влияние силы сдвига (перерезывающей) на участки, соседние с точками контакта с нагрузками.

Принималось, что динамические нагрузки оказывают влияние на более длинную часть балки, чем статические нагрузки, а влияние оси каждой колесной пары ощущается еще дальше. Следовательно, к каждой стороне балки добавлялась еще длина 0,12L, чтобы учесть динамическое воздействие нагрузок. Таким образом, оптимальная длина модели, предложенная Шахраки и др. [10], составила L_m=L+2(0,12+0,18)L (табл. 1).

Таблица 1. Параметры для моделирования подвижных нагрузок

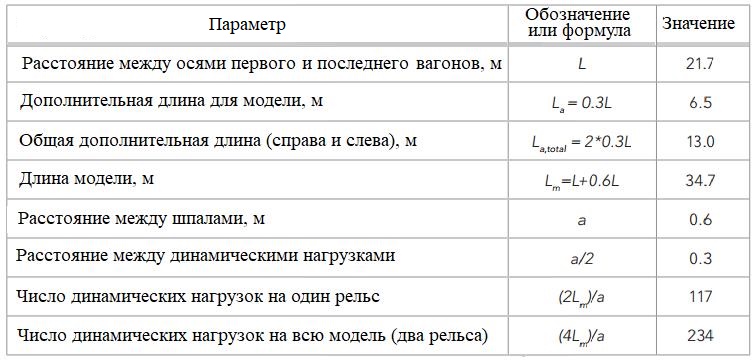
Для аппроксимации сил сдвига (перерезывающих) на стандартном железнодорожном пути авторами статьи [10] были рассмотрены балка длиной L_m и «штифтовые» опоры через каждые 60 см (a=60 см), лежащие на грунте. Динамический коэффициент определялся в PLAXIS 3D как показатель силы сдвига во времени. В рассматриваемой модели каждая отдельная динамическая точечная нагрузка имела свой собственный динамический коэффициент. Другими словами, динамическая точечная нагрузка умножалась на значение этого показателя на каждом временном шаге.

Эти коэффициенты представляют собой силы сдвига (перерезывающие) в балке, обусловленные статической нагрузкой вдоль рельса в течение определенного времени. Временной интервал динамического коэффициента должен быть достаточно малым, чтобы предотвратить ошибку в расчетах при моделировании методом конечных элементов. Шаг по времени постоянен, потому что скорость поезда и расстояние между динамическими точечными нагрузками приняты постоянными. Например, поезд со скоростью 180 км/ч проходит каждые 30 см за 0,006 с – следовательно, временной интервал должен быть выбран равным 0,006 с для фиксированных точечных динамических нагрузок.

Динамические точечные нагрузки авторы расположили на расстояниях a/2, чтобы учесть максимальные силы сдвига в середине пролетов. Они указали, что расстояние между динамическими точечными нагрузками можно уменьшить, чтобы минимизировать ошибку модели, но это увеличивает время расчета. Общее количество динамических точечных нагрузок для двух рельсов составило 4(L_m/а) (рис. 2, см. табл. 1).

Рис. 2. Размеры поезда ICE и расчетные длины для модели [10]

Далее Шахраки с соавторами [10] рассматривают пример конкретного моделирования, информация о котором представлена на рисунке 2 и в таблице 1. В этом примере скорость поезда составляет 180 км/ч, а шаг между динамическими точечными нагрузками равен 30 см. Поезд проходит каждые 30 см за 0,006 с (шаг по времени). Следовательно, оси первой колесной пары поезда требуется 0,702 с, чтобы пройти все 117 точек динамических нагрузок.

Для каждого временного шага всем точечным нагрузкам приписываются значения на основе выходных данных, полученных при расчетах в программе PROKON. Таким образом, точечные нагрузки будут активироваться непрерывно, но максимальных значений они будут достигать при прохождении над ними осей колесных пар поезда (табл. 2).

Таблица 2. Последовательность динамических коэффициентов для всех точечных нагрузок [10]

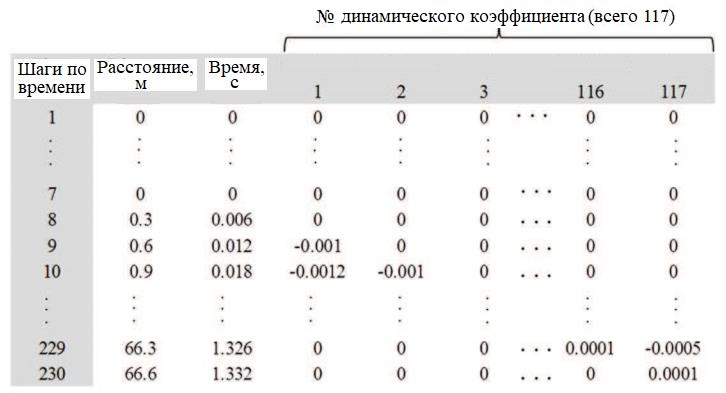
Расстояние между осями первой и последней колесной пары для поезда ICE составляет 21,7 м, что соответствует времени 0,434 с для поезда, идущего со скоростью 180 км/ч. Общее время, необходимое оси последней колесной пары для прохождения длины модели, составляет 1,136 с. Для этого промежутка времени авторами статьи [10] также учитывалось влияние поезда до входа в модель и после выхода из нее.

Дополнительное время 0,112 с, которое обозначает восемнадцать добавленных рядов к множителю, учитывалось для ослабления и предотвращения ошибок в модели при динамических вычислениях в отношении влияния отражения волны напряжения. Для моделирования границ, которые уменьшают влияние отражения волн, используются различные методы. Девять рядов коэффициентов с величинами (силами сдвига), равными нулю, вставляются в начало и в конец значений динамического коэффициента. Небольшая часть последовательности этих коэффициентов показана в таблице 2, а их изменения во времени схематично представлены на рис. 3.

Рис. 3. Графическое представление последовательности динамических коэффициентов для 117 точечных нагрузок в модели PLAXIS [10]

Шахраки с соавторами [10] выполнили статический анализ для расчета сил сдвига с применением четырех единичных точечных нагрузок на балку для моделирования четырех осевых сил одного вагона. Балка со «штифтовыми» опорами через каждые 60 см помещается на грунт. На рисунке 4 показано расположение четырех единичных точечных нагрузок, рельса и шпал в программе PROKON. Для этого расчета использовались параметры по умолчанию для PROKON (см. рис. 4). Коэффициент (модуль) реакции земляного полотна, или коэффициент постели K, отражает концептуальную взаимосвязь между давлением на грунт и прогибом (осадкой) балки. Поскольку жесткость балки обычно в десять или более раз превышает жесткость грунта, как это определено коэффициентом K, изгибающие моменты в балке и рассчитанные давления в грунте, как правило, не очень чувствительны к значению, используемому для K. Расчетная сила сдвига в балке проиллюстрирована на рис. 5. Длина модели, взятая в PROKON, была затем перемасштабирована до длины, использованной в модели PLAXIS.

Рис. 4. Масштабированная статическая модель единичных нагрузок на балку (рельс), полученная в программе PROKON [10]

Рис. 5. Сила сдвига в балке (рельсе) [10]

Длина модели по направлениям X и Y составила 35 м. Из-за геологических условий авторы статьи [10] рассмотрели модель с глубиной 11 м. Для уменьшения отражения волн на границах в модели были применены стандартные фиксированные значения и поглощающие границы. Типичный железнодорожный путь включает в себя рельсы, рельсовые скрепления и шпалы, в то время как все эти элементы пути опираются на балласт и подстилающие его слои грунтов.

Рельс моделируется с помощью балочного элемента вдоль 35-метрового профиля в направлении Y с прямоугольным поперечным сечением. Свойства балки принимаются такими же, как у рельса (UIC 60). Рельсовые скрепления моделируются как анкерные элементы между узлами. Каждая из шпал соединена с рельсом двумя рельсовыми скреплениями толщиной 30 см. Стандартная шпала B70 моделируется как элемент балки, обеспечивая момент инерции и площади. В модели размещено 68 шпал с межцентровыми расстояниями (шагом) 60 см.

Эта модель, полученная Шахраки и др. [10] в PLAXIS 3D, показана на рис. 6. Активные динамические точечные нагрузки определяются на пути 1 (см. рис. 6, б). Для лучшей визуализации 3D-модели смоделированные точечные нагрузки деактивированы на рисунках 6, а и б. На рисунке 6, в показаны примеры динамических точечных нагрузок.

Рис. 6. Детали модели [10]

Степень водонасыщения, плотность грунта, коэффициент Пуассона и модуль сдвига были получены авторами работы [10] по результатам геотехнических исследований. Эти данные были использованы для моделирования поведения грунта с помощью линейно-упругой модели и модели Мора – Кулона.

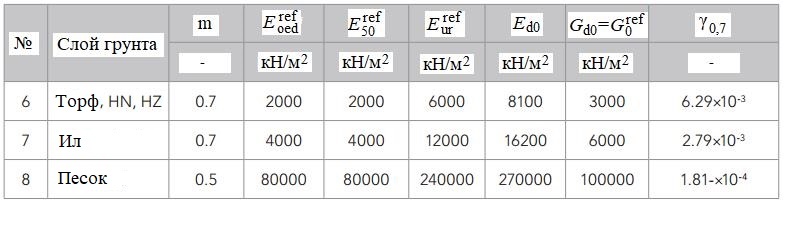
Второй вариант моделирования поведения грунта был выполнен с использованием модели упрочняющегося грунта при малых деформациях (HSS). Параметры для него были взяты по литературным данным или путем расчетов.

Шахраки и др. [10] указывают, что малые значения удельного сцепления на малой глубине для моделирования с помощью модели HSS, особенно для несвязных материалов, приводят к проблемам в результатах моделирования поверхностных слоев (малый собственный вес и низкое сцепление дают заниженное сопротивление сдвигу и потерю сходимости. – Ред.). Поэтому для верхних слоев грунта авторы статьи [10] выбрали более высокие значения сцепления (в действительности уплотненные несвязные грунты имеют эффект зацепления, который при небольших деформациях сдвига можно интерпретировать как сцепление. – Ред.). Более того, первый слой (балласт) был смоделирован с помощью модели Мора – Кулона (MC), а не HSS (из-за небольших вертикальных напряжений в верхних слоях модель упрочняющегося грунта имеет тенденцию давать нереальные результаты).

Основные и дополнительные свойства грунта, использованные в моделях, Шахраки с соавторами [10] перечислили в таблицах 3 и 4, указав, что использованный ими коэффициент Пуассона для всех слоев в модели HSS является в PLAXIS значением по умолчанию ν_ur=0,2 (подразумевается более стабильное по величине значение коэффициента при разгрузке. – Ред.)

Таблица 3. Основные свойства слоев грунта под железнодорожными путями для линейно-упругой модели (LE) и модели Мора – Кулона (MC) [10]

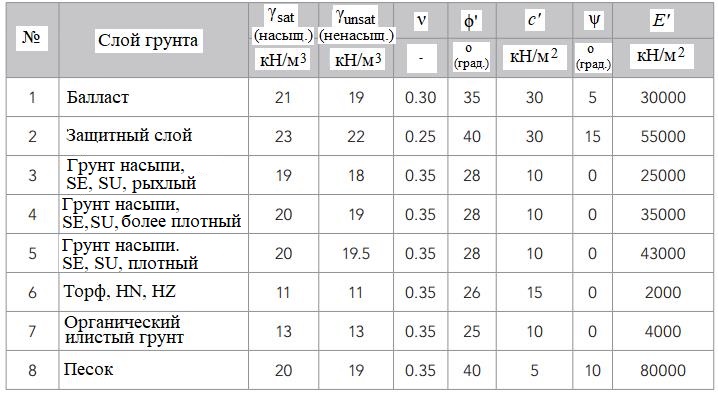
Таблица 4. Расширенные свойства слоев грунта для модели упрочняющегося грунта при малых деформациях (HSS)

Чтобы определить параметры анкерного элемента (моделирующего рельсовые скрепления), как отмечают авторы статьи [10], требуются предельные усилия и при растяжении, и при сжатии. Свойства рельсовых скреплений и необходимые параметры для моделирования элемента балки перечислены в таблицах 5 и 6.

Таблица 5. Входные данные (свойства) для рельсов и шпал в PLAXIS 3D [10]

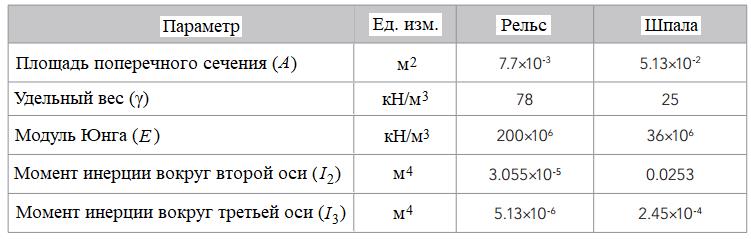
Таблица 6. Свойства рельсовых скреплений [10]

Расчеты авторов работы [10] состояли из трех этапов. Кратко охарактеризуем их.

• Первый этап – общий для создания начальных напряжений с активным уровнем грунтовых вод.
• На втором этапе выбирается дренированный тип расчета (Plastic. – Ред.). На этой стадии активируются все элементы железнодорожного пути (шпалы, рельсы и рельсовые скрепления).
• На третьем этапе (динамический тип расчета) активируются все динамические точечные нагрузки на рельсы.

Шахраки с коллегами [10] создали две модели – SIM1 и SIM2. Моделирование выполнялось для скорости поезда (одного вагона) 180 км/ч с учетом трех различных моделей грунта.

• При SIM1 для всех слоев грунта использовалась линейно-упругая модель (LE).
• При SIM2 применялась комбинация модели Мора – Кулона (MC) и модели упрочняющегося грунта при малых деформациях (HSS) (для верхних слоев грунта использовалась модель MC, а для трех самых глубоких слоев – модель HSS).

В качестве результатов авторы работы [10] представили виброскорости, а не вибросмещения, чтобы избежать повторного интегрирования, приводящего к увеличению ошибок в низкочастотной области. Они пояснили, что амплитуда скорости уменьшается при распространении волны в более глубокие слои грунта. Демпфирование материалов и границ схемы являются основными причинами уменьшения амплитуды скорости в глубоких слоях. Поэтому при моделировании оба типа демпфирования авторы [10] рассматривали с применением коэффициентов демпфирования Рэлея. Самые низкие и самые высокие соответствующие частоты зависят от свойств модели и скорости поезда. В своем исследовании [10] авторы приняли, что самые низкие и самые высокие частоты для оценки коэффициентов демпфирования Рэлея составляют от 10 до 100 Гц.

В таблице 7 сведены результаты моделирования в терминах скорости (мм/с) для четырех контрольных точек в разных слоях грунта. Шахраки и др. [10] указали, что, как и ожидается, амплитуды скорости уменьшаются с глубиной. Контрольные точки BP5 и BP6 показывают меньшие скорости, поскольку волна идет глубже в направлении Z. Изменения скорости в каждой контрольной точке при прохождении поезда для обеих моделей (SIM1 и SIM2) показаны на рисунках 7 и 8. На рисунке 9 сопоставлены рассчитанные максимальные скорости в контрольных точках для этих двух моделей. Наибольшая скорость относится к контрольной точке BP1, которая расположена на самой маленькой глубине под железнодорожным путем. При SIM2 оценивались меньшие значения для более глубоких контрольных точек, чем при SIM1, в то время как на небольшой глубине выделялась более высокая скорость по сравнению с SIM1. Однако оба моделирования показали сходные тенденции в результатах.

Таблица 7. Расчетные вертикальные скорости в различных контрольных точках для поезда, движущегося со скоростью 180 км/ч [10]

Рис. 7. Вертикальная составляющая виброскорости в контрольных точках при использовании линейно-упругой (LE) модели и скорости поезда 180 км/ч [10]

Рис. 8. Вертикальная составляющая виброскорости в контрольных точках при использовании модели Мора – Кулона (MC) и модели упрочняющегося грунта при малых деформациях (HSS) и скорости поезда 180 км/ч [10]

Рис. 9. Расчетные значения вертикальной компоненты виброскорости по глубине в контрольных точках для поезда, движущегося со скоростью 180 км/ч, при использовании моделей SIM1 на основе линейно-упругой модели (LE) и SIM2 на основе комбинации модели Мора – Кулона (MC) и модели упрочняющегося грунта при малых деформациях (HSS) [10]

Заключение

Подвижные нагрузки можно моделировать в программе PLAXIS 3D, применяя предложенный Шахраки с соавторами [10] подход и помощь вспомогательного программного обеспечения.

В своей статье [10] авторы представили предварительные результаты численного моделирования в программе PLAXIS 3D влияния подвижных нагрузок на земляное полотно, предназначенное для высокоскоростных поездов. Для этого вдоль железнодорожного пути было приложено некоторое количество точечных статических нагрузок, равных по величине осевой нагрузке (под осью колесной пары) от поезда. При этом для каждой точечной нагрузки был назначен динамический множитель (динамический коэффициент, определяющий амплитуду воздействия заданной силы), соответствующий силе сдвига во времени. Для расчета сил сдвига была смоделирована балка (рельс) под единичными нагрузками на упругом основании. Результирующие силы сдвига в балке были применены в 3D-модели как дополнительные коэффициенты динамического множителя. Кроме того, для аппроксимации динамического поведения грунтовой насыпи использовались различные модели грунта, такие как линейно-упругая (LE), Мора – Кулона (MC) и модель упрочняющегося грунта при малых деформациях (HSS).

Однако предложенный Шахраки с соавторами [10] подход имеет большое ограничение. Для определения подвижных нагрузок все множители должны быть назначены вручную для каждой динамической точечной нагрузки. Для получения более точных результатов авторы работы [10] предлагают разделить расстояние между шпалами на четыре или даже на восемь частей. Добавляя больше точечных нагрузок, можно получить более подробные результаты.

Таким образом, предложенный Шахраки и др. [10] подход обеспечивает способ исследования подвижных нагрузок в программе PLAXIS. С помощью разработанного ими метода можно моделировать и эффект взаимодействия двух поездов, которые движутся в противоположных направлениях.

Проверку достоверности своих моделей авторы статьи [10] пообещали выполнить на следующем этапе своего проекта путем сравнения с результатами экспериментов и теоретического анализа.

Хотя создание моделей нелинейного и зависящего от времени поведения грунтов является важной проблемой, многие геотехнические строительные проекты включают моделирование еще более сложных геотехнических задач, в том числе связанных с подвижными нагрузками. Поэтому авторы работы [10] высказали надежду, что будущие версии программного обеспечения PLAXIS будут оснащены специальными функциями для работы с подвижными нагрузками (и действительно, указанный функционал реализован в PLAXIS 3D начиная с версии 2018 года – Ред.).

Источники

1. В скорости и в радости. Решено вернуться к проекту ВСМ Москва – Санкт-Петербург // Коммерсантъ. 16.04.2019. URL: kommersant.ru/doc/3945517.
2. ВСМ в Петербург построят из-за нехватки пропускной способности нынешней дороги // ТАСС. 07.06.2019. URL: tass.ru/ekonomika/6525471.
3. ВСМ Москва – Санкт-Петербург // Ru.wikipedia. 25.12.2019. URL: ru.wikipedia.org/wiki/ВСМ_Москва_–_Санкт-Петербург.
4. ВСМ Москва – Санкт-Петербург должна быть построена на эстакаде // РЖДПартнер.ру. 05.08.2019. URL: rzd-partner.ru/zhd-transport/interview/vsm-moskva-sankt-peterburg-dolzhna-byt-postroena-na-estakade/.
5. Высокоскоростную магистраль Москва – Санкт-Петербург планируют открыть в 2026 году // Новые Известия. 07.10.2019. URL: newizv.ru/news/society/07-10-2019/vysokoskorostnuyu-magistral-moskva-sankt-peterburg-planiruyut-otkryt-v-2026-godu/rrr.
6. Горбунов К.В. Земляное полотно под высокоскоростное движение // СЦБИСТ. 14.05.2012. URL: scbist.com/xx1/16269-09-2010-zemlyanoe-polotno-pod-vysokoskorostnoe-dvizhenie-print.html.
7. Новый проект ВСМ Санкт-Петербург – Москва – утопия или реальность? // Транспорт в России. 23.01.2010. URL: forum.tr.ru/read.php?7,963675.
8. Путин готов изменить маршрут первой в России высокоскоростной железной дороги // ВЕДОМОСТИ. 15 апреля 2019. URL: vedomosti.ru/economics/articles/2019/04/16/799199-putin-izmenit.
9. Путин снова решил строить высокоскоростную железную дорогу Москва – Санкт-Петербург. Это даст больше места для крюковских электричек // ZELENOGRAD.RU. 17.04.2019. URL: zelenograd.ru/news/46708/.
10. Shahraki M., Sadaghiani M.R.S., Witt K.J., Meier T. 3D Modelling of Train Induced Moving Loads on an Embankment // Plaxis Bulletin. 01.10.2014. URL: plaxis.com/content/uploads/import/kb/kb-publications/Iss36%20Art2%20-%203D%20Modelling%20of%20Train%20Induced%20Moving%20Loads%20on%20an%20Embankment.pdf.

Список литературы, использованной Шахраки с соавторами при подготовке их работы [10]

• T. Dahlberg, “Railway track settlements – a literature review,” Linkцping, Sweden2004.
• C. Madshus and A. M. Kaynia, “High-Speed Railway Lines on Soft Ground: Dynamic Behaviour at Critical Train Speed,” Journal of Sound and Vibration, vol. 231, pp. 689-701, 2000.
• L. Hall, “Simulations and analyses of traininduced ground vibrations in finite element models,” Soil Dynamics and Earthquake Engineering, 2003.
• S. Witt, “The Infuence of Under Sleeper Pads on Railway Track Dynamics,” Department of Management and Engineering, Linkцping University, Sweden, 2008.
• W. Vogel, K. Lieberenz, T. Neidhart, and D. Wegener, “Zur dynamischen Stabilitдt von Eisenbahnstrecken mit Schotteroberbau auf Weichschichten,” 2011.
• B. Coelho, J. Priest, P. Holscher, and W.  Powrie, “Monitoring of transition zones in railways,” presented at the Railway Engineering Conference England, 2009.
• Y.-B. Yang and H.-H. Hung, “A 2.5D fnite/infnite element approach for modelling viscoelastic bodies subjected to moving loads,”  International Journal for Numerical Methods in Engineering, vol. 51, pp. 1317-1336, 2001.
• Prokon Software Consultants, PROKON User’s Guide: Prokon Software Consultants (Pty) Ltd.,  2010.
• M. Shahraki, “Numerical Validation of Dynamic Stability Experiments for High-Speed Railway
  Tracks,” Master of Science, Faculty of Civil Engineering - Department of Geotechnical
  Engineering, Bauhaus-Universiдt Weimar, Weimar, Germany, 2013.
• D. Rьty and K. J. Witt, Wissensspeicher Geotechnik, 18 ed. Weimar, Germany: BauhausUniversitдt Weimar, 2011.
• Plaxis bv, PLAXIS 3D 2011-Reference vol. 2. Netherlands: PLAXIS, 2011.
• P.-A. v. Wolffersdorff, “Ausgewдhlte Probleme zu statischen und dynamischen Standsicherheitsberechnungen von Staudдmmen,” 2010.
• Plaxis bv, PLAXIS 3D 2011-Material-Models vol. 3. Netherlands: PLAXIS, 2011.
• A. G. Correia, J. Cunha, J. Marcelino, L. Caldeira, J. Varandas, Z. Dimitrovovб, A. Antгo, and M. G. d. Silva, “Dynamic analysis of rail track for high speed trains. 2D approach,” in 5th Intl Worksop on Application of Computational Mechanics on Geotechnical Engineering, Portugal 2007, p. 14.