Еще раз о модели упрочняющегося грунта от ее создателей и пользователей

Геотехническое моделирование является очень важным на всех этапах современного строительства, а также при проведении мониторинга во время эксплуатации зданий и сооружений. Многие современные строительные объекты возводятся на фундаментах глубокого заложения, занимают большую площадь и передают на свои грунтовые основания значительные нагрузки, вовлекая в это очень большие объемы грунтов. Во всех частях системы «основание – фундамент – надземная часть здания/сооружения» формируется сложное напряженно-деформированное состояние (НДС), являющееся пространственно неоднородным и изменяющееся во времени в процессе строительства и эксплуатации. Его количественная оценка на всех этапах является сложной задачей и зависит от ряда факторов, в том числе от физико-механических свойств грунтов основания в условиях естественного залегания, исходного НДС массива и изменчивости модулей деформации по глубине.

Усложняющиеся со временем строительные объекты требуют совершенствования старых и разработки новых моделей (математического отображения) механического поведения грунтов и методов численного моделирования, необходимых для расчетов при геотехническом проектировании. Современные механические модели, применяемые в программных комплексах, позволяют решать эти задачи в трехмерной постановке, определять взаимное влияние зданий/сооружений и их оснований, учитывать неоднородность инженерно-геологических условий и процессы, протекающие во времени. Однако достоверность получаемых при численном моделировании численных результатов сильно зависит от правильности выбора грунтовой модели и определения ее параметров.

Одной из самых универсальных механических моделей, применяемых для описания поведения оснований, сложенных многими видами дисперсных грунтов (особенно для зданий/сооружений с фундаментами глубокого заложения, значительными дополнительными нагрузками и сложными траекториями нагружения), является упругопластическая модель с изотропным упрочнением Hardening Soil Model (HSM), или модель упрочняющегося грунта, которая была разработана в рамках классической теории пластического течения, а не теории упругости.

Первое подробное теоретическое описание этой модели было выполнено в 1999 году в докладе «Модель упрочняющегося грунта: разработка и верификация», сделанном на международном симпозиуме по вычислительной геотехнике ее разработчиками – профессором Веймарского международного исследовательского университета «Баухауз» Т. Шанцем (Германия), профессором Штутгартского университета П.А. Вермеером (Германия) и инженером компании PLAXIS b.v. П.Г. Бонньером (Нидерланды) [10]. Здесь мы приведем краткий обзор материалов этого доклада с пояснениями, взятыми из некоторых других работ [1–9].

Главными особенностями модели HS являются (рис. 1):

• гиперболическая зависимость между вертикальной относительной деформацией ε₁ и девиатором напряжений q=σ₁–σ₃ (где σ₁,σ₃ – максимальное и минимальное главное напряжение соответственно) при первичном трехосном (девиаторном) нагружении в дренированных условиях (когда грунт показывает убывающую жесткость и одновременно развиваются необратимые пластические деформации);
• линейная зависимость между этими же параметрами при разгрузке и повторном нагружении.

Рис. 1. Гиперболическая зависимость между девиаторным напряжением q=σ₁–σ₃ и относительной осевой деформацией ε₁ при первичном нагружении в процессе стандартного испытании грунта на трехосное сжатие в дренированных условиях [10]. Буквенные обозначения: E₅₀ – секущий модуль деформации первичного нагружения при 50%-ной прочности, т.е. при 50% от предельного девиаторного напряжения q_f; E_ur – модуль при разгрузке и повторном нагружении; q_a – асимптотический уровень прочности, к которому стремится зависимость; q_f – предельное девиаторное напряжение, рассчитанное по закону Кулона

Математическая формулировка модели упрочняющегося грунта использует:

• поверхность разрушения в соответствии с критерием Мора – Кулона;
• гиперболическую формулировку Дункана – Чанга для описания упругой области напряженно-деформированного состояния (с изменяемыми модулями упругости для траектории первичного нагружения и для траектории разгружения и повторного нагружения);
• две функции текучести – для девиаторного и изотропного нагружений (для описания пластических сдвиговых и объемных деформаций)

Модель упрочняющегося грунта дает возможность моделировать нелинейность деформаций, остаточные перемещения при разгрузке и отражает переуплотнение грунтов основания с помощью коэффициента переуплотнения OCR.

HSM позволяет более достоверно описывать поведение грунтовых оснований, чем модель Мора – Кулона (последняя хорошо подходит только для описания допредельных состояний грунта, поскольку не учитывает изменения модуля деформации при изменении уровня напряжений в массиве, а также при разгрузке и повторном нагружении грунта и занижает значения дополнительных осадок фундамента).

В отличие от идеально-упругопластической модели с критерием прочности Мора – Кулона, положение поверхности текучести (границы области допустимых напряжений для сохранения упругого поведения) в модели упрочняющегося грунта не является фиксированным в пространстве главных напряжений. Ограниченное ею пространство упругого поведения может расширяться вследствие пластического деформирования. При этом модель подразумевает различие между двумя основными видами упрочнения – при сдвиге и при сжатии. Она учитывает в том числе зависимость модуля жесткости (деформации) от напряжений, поэтому все параметры жесткости в ней увеличиваются с ростом давления.

Модель упрочняющегося грунта достаточно хорошо описывает развитие сдвиговых деформаций при девиаторном нагружении и объемных деформаций при всестороннем обжатии. Она достаточно точно отражает поведение грунта при экскавации, устройстве подпорных стен и проходке туннелей, когда происходит уменьшение среднего эффективного напряжения и одновременно мобилизация сопротивления пород сдвигу. Ограничения этой модели заключаются в том, что она не очень подходит для расчетов оснований, сложенных слабыми сильносжимаемыми грунтами, непригодна для моделирования динамических процессов и не может учесть анизотропию прочности и жесткости, а также ползучести и длительной прочности. Следует также отметить, что HSM не учитывает разупрочнение грунта в результате эффектов дилатансии (изменений объема, наблюдаемых в дисперсных материалах, когда они подвергаются сдвиговым деформациям). Поэтому для высокоточного моделирования циклического нагружения требуются более сложные модели.

HSM использует три модуля деформации:

• секущий при 50%-ной прочности (E₅₀), учитывающий жесткость при девиаторном нагружении в процессе трехосного сжатия;
• одометрический (E_oed), учитывающий жесткость при всестороннем и компрессионном сжатии;
• модуль разгрузки и повторного нагружения (E_ur).

При этом каждый из этих модулей меняется в зависимости от текущей величины наименьшего главного напряжения σ₃, которое в случае трехосных испытаний равно величине всестороннего давления.

Суммарные деформации в HSM рассчитываются с использованием зависимой от нагрузки жесткости, различной для первичного нагружения и для разгрузки и повторного нагружения. Эти пластические деформации вычисляются путем введения мультиповерхностного критерия пластичности (текучести). Принимается, что упрочнение является изотропным в зависимости как от пластического сдвига, так и от объемной деформации. Закон пластического течения принимается неассоциированным для фрикционного упрочнения при сдвиговом деформировании и ассоциированным для упрочнения на шатровой поверхности текучести в модифицированной модели Друкера – Прагера (кэп-модели – cap-model) – не зависящей от скорости нагружения упругопластической модели, которая предполагает материал однородным и изотропным.

Упрочнение при сдвиге происходит при первичном девиаторном нагружении. Оно используется для моделирования необратимых деформаций. Величины пластических деформаций, связанных с поверхностью текучести при сдвиге, в значительной степени контролируются трехосным модулем деформации E₅₀^ref, соответствующим эталонному всестороннему давлению, равному бытовому давлению.

Поверхности текучести в ходе сдвигового упрочнения показаны на рисунке 2. Кривые текучести по мере деформирования поднимаются до предельной кривой Мора – Кулона. Их форма зависит от показателя степени m в формуле, отражающей зависимость жесткости (модуля деформации E₅₀) от напряжения (формула (3) в табл. 1). При m=1 линии получаются прямыми, а при m<1 – слегка изогнутыми.

Рис. 2. Поверхности текучести в ходе сдвигового упрочнения твердого грунта при показателе степени m в зависимости жесткости от напряжения, равном 0,5. Значения параметра упрочнения (пластической деформации сдвига γ^p) возрастают для кривых снизу-вверх. При построении таких кривых текучести нужно использовать уравнения (3), (4), (7), (8) из табл. 1 [10]

Упрочнение при сжатии можно представить в виде эллиптической поверхности текучести (называемой в разных публикациях «шатром» или «шапкой» – cap) (рис. 3, 4), которая характеризуется двумя параметрами – эквивалентным давлением изотропного предварительного уплотнения p_p и вспомогательным модельным параметром α, принимаемым в программе Plaxis равным (1–sinφ), где φ – угол внутреннего трения грунта. Величины пластических деформаций, связанных с шатровой поверхностью текучести, в значительной степени контролируются одометрическим модулем деформации E_oed^ref. Увеличение «шапки» при нагружении будет сопровождаться объемной пластической деформацией и упрочнением.

На рисунке 3 заштрихована упругая зона, ограниченная поверхностью текучести при сдвиге (линия над заштрихованной областью) и поверхностью текучести при сжатии с соответствующей объемной пластической деформацией (эллиптическая линия справа от заштрихованной зоны). Стрелками показаны направления смещения этих границ при сдвиговом (сверху) и объемном (справа) упрочнении. Указанные две поверхности текучести, объединенные в одно целое, и дали возможность разработать модель с независимыми входными данными – E₅₀ и E_oed. На рисунке 4 упругая зона, ограниченная этими поверхностями, показана в объеме.

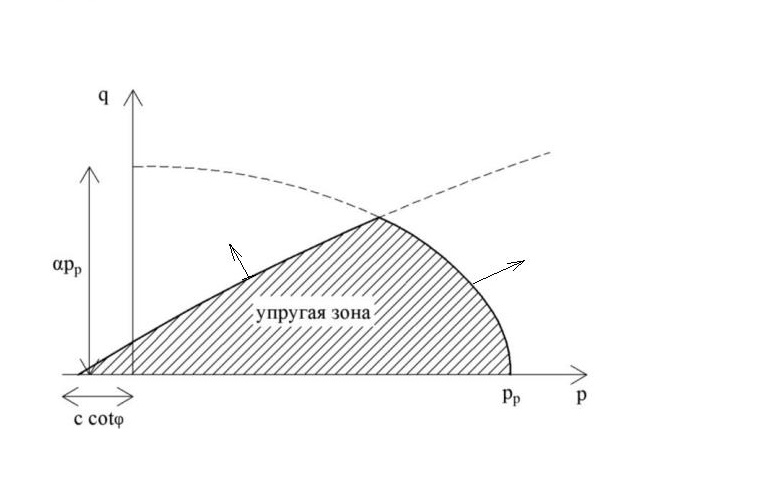
Рис. 3. Упругая зона, ограниченная поверхностью текучести при сдвиге (линия над заштрихованной областью) и поверхностью текучести при сжатии с соответствующей объемной пластической деформацией (эллиптическая линия справа от заштрихованной зоны). Стрелками показаны направления смещения поверхностей текучести при сдвиговом (сверху) и объемном (справа) упрочнении [1, 10]

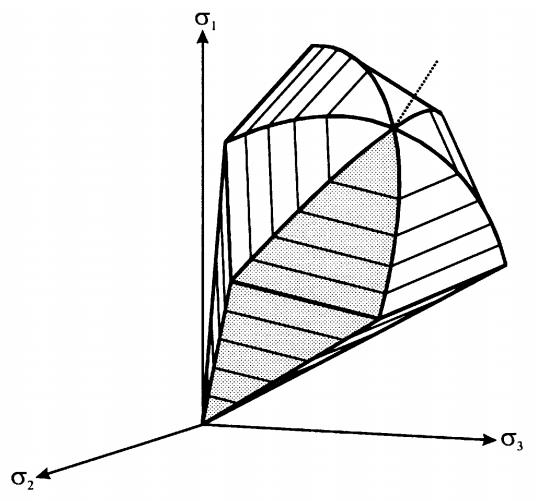
Рис. 4. Трехмерное представление суммарной поверхности текучести для модели упрочняющегося грунта в пространстве главных напряжений для несвязного грунта [10]

Модель упрочняющегося грунта записывается в виде ряда математических выражений – прежде всего основных уравнений для модулей жесткости, пластического течения (текучести), разрушения и поверхностей текучести, которые совпадают с поверхностями потенциала пластической деформации для устойчиво пластического материала (табл. 1, 2).

Модель HS можно использовать для расчетов в том числе в программном комплексе PLAXIS на основе метода конечных элементов (МКЭ).

Численное моделирование с использованием HSM по сравнению с моделью Мора – Кулона требует больше входных параметров, для определения которых помимо стандартных компрессионных испытаний необходимо выполнить трехосные испытания в консолидировано-дренированных условиях с использованием стабилометров. Об определении параметров для численного моделирования поведения дисперсных грунтов с использованием модели упрочняющегося грунта хорошо рассказано в статье [5].

Для использования этой модели необходимо задать следующие основные параметры:

1) параметры прочности:

• удельное сцепление с;
• угол внутреннего трения φ;
• угол дилатансии Ψ (по умолчанию в программе Plaxis он равен нулю);

2) параметры жесткости:

• секущий модуль деформации (или секущий модуль жесткости, как его называют разработчики HSM [10]) при стандартном испытании грунта на трехосное сжатие в дренированных условиях E₅₀^ref;
• касательный модуль деформации (или касательный модуль жесткости, как его называют разработчики HSM [10]) при первичном одометрическом нагружении E_oed^ref (в программе Plaxis по умолчанию E_oed^ref=E₅₀^ref);
• показатель степени m в формуле (3) в табл. 1, выражающей зависимость жесткости от уровня напряжений (в программе Plaxis по умолчанию m=0,5).

3) дополнительные параметры:

• жесткость при разгрузке и повторном нагружении E_ur^ref (в программе Plaxis по умолчанию E_ur^ref=3E₅₀^ref);
• коэффициент Пуассона ν_ur при разгрузке и повторном нагружении (в программе Plaxis по умолчанию он равен 0,2);
• эталонное всестороннее давление (напряжение) грунта в условиях естественного залегания p^ref, равное бытовому давлению (в программе Plaxis по умолчанию оно равно 100 кН/м²);
• коэффициент горизонтального напряжения при нормальной консолидации K₀^nc (в программе Plaxis по умолчанию он равен (1–sinφ));
• коэффициент разрушения R_f=q_f/q_a, где q_f – предельное девиаторное напряжение являющееся пределом деформирования и рассчитанное по закону Кулона, q_a – асимптотический уровень прочности, к которому стремится зависимость между напряжениями и деформациями (см. рис. 1) (в программе Plaxis коэффициент R_f по умолчанию равен 0,9);
• прочность на растяжение σ_tension (в программе Plaxis она по умолчанию равна нулю).

Однако приступать к созданию модели упрочняющегося грунта можно, имея три экспериментально определенных параметра – с, φ, E₅₀^ref (или E_oed^ref). Как уже было отмечено выше, параметры деформируемости для HSM определяются на основе результатов консолидированно-дренированных трехосных и компрессионных испытаний.

Остальные параметры можно принять по рекомендациям разработчиков [8, 10].

Модель упрочняющегося грунта была откалибрована ее разработчиками [10] путем обратного расчета результатов трехосных и одометрических испытаний рыхлого «хостунского» песка (с начальным коэффициентом пористости e₀=0,89), параметры которого хорошо известны и для которого имеется много доступных экспериментальных данных, поскольку он часто используется в геотехнических исследованиях. С помощью HSM и компьютерной программы Plaxis на основе МКЭ были получены численные модели испытаний на недренированный сдвиг и прессиометрических испытаний в калибровочной камере. Для обеих проверок модели экспериментальные и численные результаты оказались довольно близкими друг к другу, что авторы работы [10] сочли очень перспективным.

С помощью такой откалиброванной модели удобно выполнять обратные расчеты результатов испытаний на недренированный сдвиг и прессиометрических тестов.

Предложенная в работе [10] модель упрочняющегося грунта оказалась весьма привлекательной для использования в повседневной геотехнической практике. С точки зрения ее авторов, дальнейшие разработки должны были бы включать расширение базы данных в поле параметров жесткости для связных грунтов, применение предложенной модели для решения краевых задач (нахождения предельных значений), в которых актуальна жесткость при малых деформациях, а также трехмерную верификацию модели. И эти разработки с момента предложения HSM активно проводятся разными авторами во всем мире.

Таблица 1. Уравнения из работы разработчиков модели упрочняющегося грунта [10]

Таблица 2. Параметры, используемые в описании модели упрочняющегося грунта из работы ее разработчиков [10]

Список литературы и других источников

1. Кудашева М.И., Калошина С.В. Сравнение модели Мора – Кулона и модели упрочняющегося грунта в программном комплексе Plaxis // Строительство и архитектура. Опыт и современные технологии. 2017. № 9. URL: http://sbornikstf.pstu.ru/council/?n=&s=501.
2. Мирный А.Ю. и др. Механические модели грунтов hardening soil и soft soil – области применения // Geoinfo.ru. 11.04.2017. URL: https://www.geoinfo.ru/product/mirnyj-anatolij-yurevich/mekhanicheskie-modeli-gruntov-hardening-soil-i-soft-soil-oblasti-primeneniya-35132.shtml.
3. Орехов В.В., Орехов М.В. Использование модели упрочняющегося грунта для описания поведения песка различной плотности при нагружении // Вестник МГСУ. 2014. № 2. URL: https://cyberleninka.ru/article/n/ispolzovanie-modeli-uprochnyayuschegosya-grunta-dlya-opisaniya-povedeniya-peska-razlichnoy-plotnosti-pri-nagruzhenii.
4. Смелянский Р.И. Математическое моделирование процессов компактирования и экструзии низкотемпературных термоэлектрических материалов: магистерская диссертация. СПб.: Изд-во Санкт-Петербургского политехнического университета, 2017.
5. Строкова Л.А. Определение параметров для численного моделирования поведения грунтов // Известия Томского политехнического университета. Технология и техника геологоразведочных работ. 2008. Т. 313. № 1. URL: https://www.lib.tpu.ru/fulltext/v/Bulletin_TPU/2008/v313/i1/12.pdf.
6. Тер-Мартиросян З.Г. и др. Экспериментально-теоретические основы проектирования фундаментов глубокого заложения высотных зданий с учетом OCR и POP: презентация МГСУ // Fc-union.com. 15.06.2015. URL: http://fc-union.com/wp-content/uploads/2015/06/Prezentatsiya-MGSU.pdf.
7. http://proofoil.ru/Oilproduction/Borewell4.html.
8. PLAXIS. Finite element code for soil and rock analyses. Rukovodstvo pol'zovatelia. 3D Foundation Versiia 2.
9. Schanz T., Vermeer P.A. On the stiffness of sands // Gйotechnique. Vol. 48. P. 383–387.
10. Schanz T., Vermeer P.A., Bonnier P.G. The hardening soil model: formulation and verification // Proceedings of the International Plaxis symposium “Beyond 2000 in computational geotechnics”. Rotterdam: Balkema, 1999. P. 281–296.

Кстати, для желающих больше узнать о работе модели HS и других моделей, проводится множество курсов повышения квалификации. Мы рекомендуем курсы в геотехнической лаборатории АО «МОСТДОРГЕОТРЕСТ». Подробнее о них можно узнать на официальном сайте организации www.mdgt.ru

Заглавное фото предоставлено АО «МОСТДОРГЕОТРЕСТ».