Обзор работы Вермеера и Де Борста о неассоциированной пластичности грунтов и бетона. Часть 2
Продолжаем знакомить читателей с важной для геотехников работой Вермеера и Де Борста "Неассоциированная пластичность для дисперсных грунтов, бетона и скальных пород" [2], написанной по литературным и собственным данным и опубликованной в 1984 году в журнале Heron (Нидерланды) на английском языке. В первой части [1] мы рассмотрели общее содержание этой весьма объемной статьи. Здесь более подробно остановимся на разделах, посвященных дилатансии и трехосным испытаниям.
О значении дилатансии
Дилатансию П.А. Вермеер и Р. Де Борст описывают в своей работе [2] как изменение объема материала, связанное с деформацией под действием напряжения сдвига его элемента, принимаемого достаточно большим, то есть содержащего много частиц в качестве микроэлементов.
Для того чтобы представить себе, как происходит дилатансия, авторы предлагают рассмотреть группу несжимаемых сфер, упакованных максимально плотно. Если происходит любая сдвиговая деформация, относительные положения сфер должны измениться и общий объем этой группы должен увеличиться. И наоборот, если эта группа изначально была в максимально неплотно упакованном состоянии, деформация сдвига приведет к уменьшению ее общего объема. Примерно это и наблюдается как для дисперсных грунтов, так и для сцементированных зернистых материалов (скальных пород, бетона).
Для характеристики дилатантного материала используется угол дилатансии Ψ, в случае простого сдвига представляющий собой отношение пластического изменения объема к пластической сдвиговой деформации. Авторы указывают, что при испытании конкретного материала величина Ψ оказывается постоянной вблизи и в момент достижения пиковой прочности. При этом они напоминают, что для дисперсных грунтов, как известно, угол дилатансии значительно меньше угла внутреннего трения, однако указывают, что для бетона и скальных пород ситуация является сходной (что обещают показать в своей работе позже).
Далее Вермеер и Де Борст рассматривают примеры необходимых для практики задач, чтобы помочь читателям оценить важность угла дилатансии. Для простоты они идеализируют зернистый материал, принимая кривую «напряжение – деформация» для него билинейной (рис. 1). Эта основополагающая модель включает пять параметров материала: удельное сцепление c, угол внутреннего трения φ и параметры деформации – модуль Юнга E, коэффициент Пуассона v и угол дилатансии Ψ.
![Рис. 1. Билинейная идеализация результатов трехосных испытаний [2]](/images/dynamic/img41003.jpg)
Задача 1. Нагрузка от круглой фундаментной плиты является классической проблемой в механике грунтов. Поэтому авторы рассматривают пример вдавливания в зернистый материал жесткой круглой пластины (рис. 2, врезка). Пластину они приняли идеально гладкой, а зернистый материал – изначально не подвергавшимся нагрузкам. Весом этого материала они пренебрегли. С целью изучения роли угла дилатансии Вермеер и Де Борст провели анализ методом конечных элементов для двух разных его значений, одно из которых не дает дилатансии вообще, а другое дает чрезвычайно высокую ее степень. При этом начальные наклоны кривых «нагрузка – смещение» для этих двух величин совпадают (см. рис. 2), так как в начале нагружения материал ведет себя совершенно упругим образом.
![Рис. 2. Результаты использования метода конечных элементов для случая вдавливания жесткой гладкой круглой пластины в зернистый материал, до этого не подвергавшийся нагрузкам. Предельная нагрузка не зависит от угла дилатансии [2]](/images/dynamic/img41004.jpg)
Из-за концентрации напряжений зоны пластичности развиваются вблизи края вдавливаемой под действием постоянной нагрузки пластины. Авторы отмечают, что дилатансия влияет на поведение и распространение пластических зон (о чем обещают более подробно рассказать в своей работе позже). Действительно, из рисунка 2 можно увидеть, что с увеличением нагрузки кривые «нагрузка – смещение» для двух указанных углов дилатансии все больше отклоняются друг от друга. Реакция сильного дилатанта намного жестче по сравнению с недилатантным материалом. При некотором уровне напряжения зоны пластичности распространяются под пластину. И в конце концов происходит разрушение.
Несмотря на различия в поведении «нагрузка – деформация», похоже, что обеим вышеупомянутым кривым соответствует одинаковая разрушающая нагрузка, которая показана на рисунке 2 штрих-пунктирной линией. Авторы считают, что на такую расчетную предельную нагрузку можно смело полагаться, поскольку она хорошо согласуется с жестко-пластическим полуаналитическим решением Кокса с соавторами (Cox et al., 1961), в соответствии с которым среднее давление на пластину при разрушении для сильнодилатантного материала составляет 20,1с (где с – удельное сцепление материала). Расчет же методом конечных элементов дает не только предельную нагрузку, но и полную кривую «нагрузка – смещение».
Вермеер и Де Борст отмечают, что рассмотренный пример нагрузки от вдавливания пластины является несколько искусственным, поскольку ее подошва была принята идеально гладкой. В такой ситуации материал под пластиной более или менее свободно перемещается к ее краю, вызывая подъем соседней поверхности.
В соответствии с приведенным в начале раздела определением дилатансии, для конкретной деформации сдвига материал с более высоким углом дилатансии должен больше увеличиваться в объеме по сравнению с материалом с меньшим значением этого параметра. Если же, как в приведенном выше примере, материал может свободно течь под пластиной к близлежащей свободной поверхности, то будет наблюдаться только несколько более жесткое поведение для более дилатантного материала, но не будет или почти не будет влияния на предельную нагрузку.
Однако если материал не может легко перемещаться к ближайшей границе пластины (как например, на практике для глубоко закрепленных в грунте анкеров или ребристых стальных арматурных стержней в массивных бетонных конструкциях), то предельная нагрузка будет зависеть от интенсивности дилатансии. Для таких кинематически ограниченных задач разрушающая нагрузка для более дилатантного материала будет более высокой (что авторы обещают более подробно объяснить в своей работе далее).
Задача 2. Второй приведенный авторами пример касается кинематически немного более ограниченной конфигурации – вдавливания круглого конуса в песок (рис. 3, врезка). Как и в первой задаче, реакция материала с увеличением угла дилатансии становится жестче, его несущая способность также увеличивается.
![Рис. 3. Результаты использования метода конечных элементов для случая вдавливания конуса в песок. Предельная нагрузка зависит от угла дилатансии [2]](/images/dynamic/img41005.jpg)
Вермеер и Де Борст отмечают, что в строительной механике кинематически ограниченные ситуации встречаются реже, чем в механике грунтов. Для бетонных балок и плит дилатансия настолько легко переносится к близлежащим границам, что угол дилатансии не влияет на разрушающие нагрузки. Для соответствующих одномерных и двумерных построений анализ граничных условий может быть выполнен только на основе параметров прочности, а результаты такого анализа могут уверенно использоваться в большинстве случаев, несмотря на то что теоремы Койтера (Koiter, 1960) о верхней и нижней границах в теории пластичности, строго говоря, больше не имеют силы. Однако для действительно трехмерных построений снова можно ожидать, что угол дилатансии влияет на несущую способность, и это было подтверждено авторами в их более ранней публикации при анализе поведения купольной конструкции, показанной на рисунке 4, с использованием компьютерной программы DIANA и других примеров с использованием конечноэлементной программы PLAXIS.
![Рис. 4. Результаты использования метода конечных элементов для купольной конструкции. Ассоциированная пластичность занижает смещение [2]](/images/dynamic/img41006.jpg)
О трехосных испытаниях
Вермеер и Де Борст указывают, что для бетона наиболее широко используются испытания на одноосное сжатие. Простым их продолжением являются испытания на трехосное сжатие, которые нашли широкое применение для дисперсных грунтов.
Авторы отмечают, что в идеале трехосные тесты должны позволять независимо управлять всеми тремя главными напряжениями (рис. 5, a), но тогда они требуют довольно сложных приборов, что почти исключает возможность их использования в иных целях, кроме исследовательских.
Поэтому для решения практических задач чаще проводят испытания цилиндрических образцов в обычных трехосных приборах, хотя такие тесты и не являются истинно трехосными. В этом случае образцы находятся в резиновой водонепроницаемой мембране внутри испытательной камеры, где они могут подвергаться воздействию гидростатического давления. Затем увеличивается и становится основным осевое сжимающее напряжение. Другие напряжения остаются равными давлению боковых стенок ячейки (рис. 5, б). (Таким образом, одноосное испытание можно было бы представить как трехосное без давления стенок ячейки.)
![Рис. 5. Кубический образец для истинного трехосного испытания (а) и цилиндрический образец для испытания в обычном трехосном приборе (б) [2]](/images/dynamic/img41007.jpg)
Общий рисунок результатов таких трехосных испытаний практически одинаков для дисперсного грунта, скальных пород и бетона. Авторы показали характерную кривую «напряжение – деформация» по данным стандартного трехосного теста на рис. 6, а. Они выделили на этом графике три участка:
I – почти линейный;
II – имеющий монотонно убывающий положительный наклон;
III – имеющий отрицательный наклон после максимума кривой.
С точки зрения теории пластичности эти участки соответствуют упругому, упрочняющемуся и разупрочняющемуся (ослабляющемуся) поведению материала соответственно (см. рис. 6).
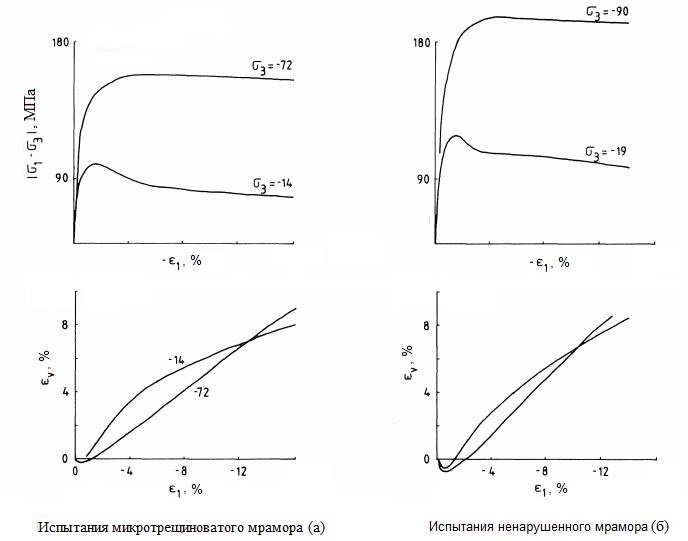
Для трещиноватых скальных пород кривая «напряжение – деформация» может быть сначала вогнутой из-за закрытия микротрещин в начале нагружения (рис. 7).
![Рис. 6. Типичные результаты трехосного испытания для несвязного или сцементированного зернистого материала [2]](/images/dynamic/img41008.jpg)
![Рис. 7. Результаты испытаний на одноосное сжатие для скальной породы [2]](/images/dynamic/img41009.jpg)
Далее авторы обсуждают упомянутые выше три участка кривой «напряжение – деформация» более подробно.
I. Упругая область. В начале нагружения поведение образца может быть аппроксимировано как упругое, так как в этом случае все его деформации в случае снятия нагрузки восстанавливаются. Здесь в цикле «нагружение – разгрузка» наблюдается настолько малый гистерезис, что процессы рассеяния энергии пренебрежимо малы. В такой ситуации в образце бетона мало или нет микротрещин, а в образце дисперсного грунта почти нет перегруппировки частиц – следовательно, можно применить закон Гука.
Если принять изотропность, то для описания поведения материала достаточно двух констант – модуля Юнга E и коэффициента Пуассона v. Для бетона значения E находятся в диапазоне 20–40 ГПа, что примерно в 1000 раз больше, чем для песка. Для скальных пород величины E могут или приближаться к таковым для песка, или превышать таковые для бетона в зависимости от пористости материала.
А для коэффициента Пуассона согласованность для этих трех типов материала лучше. Большинство известных из публикаций значений v для бетона находится в диапазоне 0,15–0,2, а для дисперсных грунтов – в несколько более широком диапазоне (0,0–0,3). Величина v может быть определена только в том случае, если измерены как осевая деформация, так и горизонтальная. Однако при испытаниях дисперсного грунта вместо горизонтальной обычно измеряется объемная деформация.
II. Область упрочнения. Инициирование упрочняющегося поведения является постепенным и нечетко определенным. На этом этапе испытания деформация становится все более неупругой из-за появления микротрещин в бетоне, скальной породе или из-за скольжения частиц в дисперсном грунте. В этом случае использование нелинейной упругости могло бы привести к противоречивому и неточному описанию поведения материала, поскольку такие теории предсказывают постоянное сжатие образца при постоянном нагружении. Но такой прогноз опровергается экспериментальными данными (см. рис. 6, б), которые показывают дилатантное увеличение объема при дальнейшем нагружении до определенного момента, что характерно, как подчеркивают авторы, не только для песчаных грунтов, но и для бетона и скальных пород. Это явление вызвано фрикционным проскальзыванием частиц (их групп) или вдоль других частиц в дисперсном зернистом грунте, или вдоль микротрещин в сцементированном зернистом материале (рис. 8).
![Рис. 8. Фрикционное проскальзывание по микротрещинам (а) или между группами частиц (б). Оба случая приводят к увеличению объема (дилатансии) [2]](/images/dynamic/img41010.jpg)
Затем авторы вводят некоторые концепции из теории пластичности, которые будут нужны для более строгого описания дилатансии в дальнейшем. Прежде всего это основное исходное допущение

в соответствии с которым скорость общей деформации является суммой упругого (верхний индекс e) и пластического (верхний индекс p) вклада в нее. Набор буквенного обозначения жирным шрифтом означает, что мы имеем дело со столбцовой матрицей, а точка над ним означает материальную производную по времени. Авторы отмечают, что читателей, не знакомых с теорией пластичности, эта точка может озадачить, поскольку в обычной теории пластичности время не учитывается, а просто служит параметром, который контролирует последовательность нагружения (поэтому не учитывается влияние вязкости, то есть, по существу, используется модель невязкого материала).
Ближе к концу области упрочнения осевое напряжение почти не увеличивается. И это означает, что скорость упругой деформации практически равна нулю, так что все последующие приращения деформации имеют пластическую природу. Тогда существует линейная зависимость между изменениями объема и осевой деформации (см. рис. 6, в) – скорость увеличение объема оказывается постоянной. Это наблюдение можно представить с помощью следующих уравнений:
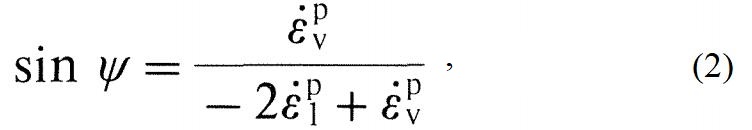
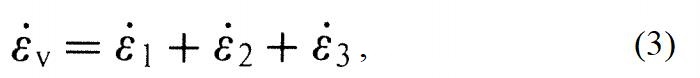
где Ψ является константой, обычно и называемой углом дилатансии.
Здесь Вермеер и Де Борст отмечают, что в публикациях по механике грунтов угол дилатансии для условий плоской деформации определяется с использованием другого уравнения, а предложенная ими новая формула (2), полученная по результатам трехосных испытаний, справедлива для условий и трехосного сжатия, и плоской деформации. Это авторы обещают подробнее рассмотреть в своей работе позже. Используя уравнение (2) и имеющиеся данные испытаний, они также обещают показать необходимость применения в подобных ситуациях теории неассоциированной пластичности вместо ассоциированной, о чем (по крайней мере для бетона) было много споров до написания обсуждаемой статьи в силу, вероятно, недостатка экспериментальных данных.
III. Область разупрочнения (ослабления, уменьшения прочности). Кривые «напряжение – деформация» по данным обычных трехосных тестов показывают наличие максимумов, которые ярко выражены для плотных песков, а также для скальных пород и бетона при испытаниях с низкими всесторонними (ограничивающими) давлениями, но являются очень сглаженными в случае рыхлых песков, а также для бетона и скальных пород при испытаниях с высокими всесторонними давлениями.
Указанные ярко выраженные пики частично объясняются тонкими полосами сдвига (или разломами), которые разделяют образец на два более или менее твердых тела. Для таких макроскопических неоднородных деформаций результаты их измерений уже не являются объективными. Эта ситуация сравнима с сужением поперечного сечения (образованием шейки) стального стержня при его испытании на растяжение, когда его длина влияет на измеренную деформацию.
Сходным образом разрывное нарушение или выгибание образцов при испытаниях на трехосное сжатие приводят к ярко выраженным пикам и необъективным результатам измерения деформаций. Как следствие, последние участки кривых «напряжение – деформация» на рисунке 6, а и б нельзя использовать для получения материальных констант. Более полезной в этом отношении является кривая «осевая деформация – объемная деформация», показанная на рисунке 6, в, поскольку, хотя приращения деформации и измеряются неправильно, соотношение скоростей деформирования не так сильно зависит от локализации в полосе сдвига. Следовательно, угол дилатансии с помощью такой кривой может быть оценен с приемлемой точностью, несмотря на неоднородность деформаций.
Авторы предполагают, что результаты обычных испытаний на трехосное сжатие не являются надежными в области разупрочнения из-за того, что практически невозможно удерживать равномерно деформированный образец в этом диапазоне. Они ссылаются на испытания очень плотного песка, выполненные Хеттлером и Вардолакисом (Hettler, Vardoulakis, 1984), с более объективными измерениями деформаций. Кривые «напряжение – деформация», полученные в результате этих испытаний, имели очень сглаженные максимумы (рис. 9, a). Это убедительно свидетельствует о том, что ярко выраженные пики для плотного песка, которые обнаруживаются при обычных трехосных испытаниях, действительно в значительной степени вызваны полосами сдвига и другими неоднородными деформациями. Для бетона ситуация является более сложной из-за возникновения трещин по типу растяжения, когда образец испытывается при низких давлениях в ячейке. Однако при более высоких давлениях бетон и дисперсные грунты снова демонстрируют сходное поведение.
![Рис. 9. Результаты трехосных испытаний плотного песка [2]](/images/dynamic/img41011.jpg)
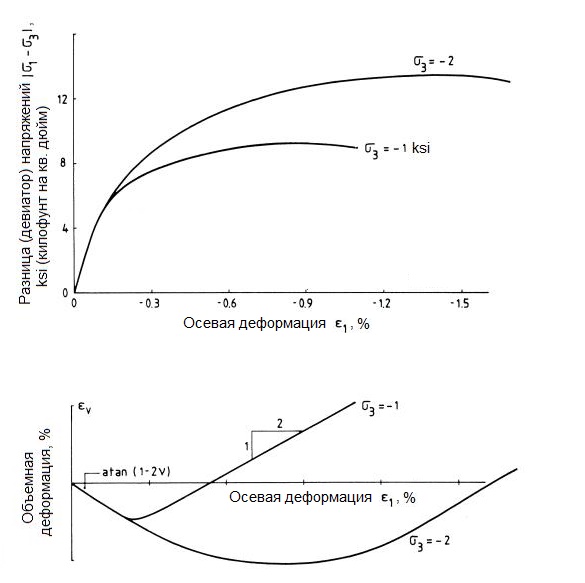
На рисунке 9, б авторы привели кривую «осевая деформация – объемная деформация» по данным Хеттлера и Вардолакиса для плотного песка. На основе этого графика можно определить, что наклон равен минус 0,7 для соотношения

Эту величину можно подставить в уравнение (2) и получить значение угла дилатансии, равное 15 град. Оно является типичным для очень плотного песка, в то время как рыхлые пески имеют углы дилатансии всего в несколько градусов, а нормально консолидированные глины не проявляют дилатансию вообще.
Для бетона и скальных пород наблюдается, по существу, такая же тенденция, что авторы продемонстрировали с помощью рисунков 10 и 11. На них показаны графики для некоторых скальных пород и бетона, которые аналогичны графику на рисунке 9, б. Применяя формулу (2), можно получить значения угла дилатансии для скальных пород в диапазоне 12–20 град. Далее авторы ссылаются на испытания Михелиса (Michelis, 1981) с давлениями в ячейке около 200 МПа, которые дали углы дилатансии 6–9 град. при чрезвычайно больших давлениях. Для высокопрочного бетона (рис. 11) может быть получен угол дилатансии, равный 13 град. Как и для скальных и дисперсных грунтов, дилатансия как высокопрочного, так и низкопрочного бетона исчезает при высоких всесторонних давлениях.
Таким образом, как предполагают авторы, все значения угла дилатансии приблизительно укладываются в диапазон 0–20 град. независимо от того, имеем ли мы дело с дисперсным грунтом, скальной породой или бетоном. Конечно, материал не может расширяться («дилатировать») бесконечно. Наблюдения подтверждают, что после интенсивного сдвига угол дилатансии постепенно исчезает и любой последующий сдвиг больше не вызывает изменений объема.
О параметрах прочности
Вермеер и Де Борст отмечают, что данные трехосных испытаний, выполненных при различных давлениях в ячейке, показывают увеличение максимальной прочности с ростом давления. С инженерной точки зрения критерий линейной прочности (где a и b – константы)

обычно достаточно точен. Его можно переписать следующим образом:
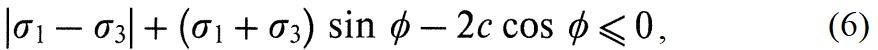
где c – удельное сцепление материала; φ – угол внутреннего трения.
Для дисперсных грунтов большинство значений угла внутреннего трения находится в диапазоне 15–45 град., причем величины до 30 град. являются типичными для глин, а более высокие – для песков. Для бетона большинство представленных в публикациях значений находится в диапазоне 30–35 град.
Из-за этого довольно узкого диапазона удельное сцепление почти полностью определяется силой одноосного сжатия:
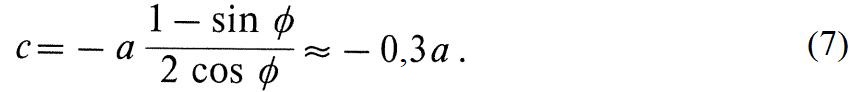
При этом авторы отмечают, что сжимающие напряжения рассматриваются как отрицательные, поэтому константа a в критерии прочности (5) является отрицательной.
Данные, представленные на рисунке 9, а, хорошо соответствуют параметрам a=0 и b=5,3. Расчет с этими значениями дает c=0 и φ=43 град., что типично для очень плотного песка.
Таким образом, как указывают авторы, и для дисперсных грунтов, и для скальных пород, и для бетонов угол внутреннего трения, как правило, намного больше, чем угол дилатансии. И это подразумевает, что для указанных материалов должна использоваться теория неассоциированной пластичности.
Продолжение обзора статьи Вермеера и Де Борста будет приведено в следующей части.
Список литературы
1. Обзор работы Вермеера и Де Борста о неассоциированной пластичности грунтов и бетона. Часть 1. Общее содержание // Geoinfo.ru. 17.06.2019. URL: https://www.geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/obzor-raboty-vermeera-i-de-borsta-o-neassociirovannoj-plastichnosti-gruntov-i-betona-chast-1-obshchee-soderzhanie-40928.shtml.
2. Vermeer P.A., De Borst R. Non-associated plasticity for soils, concrete and rock // Heron. 1984. Vol. 29. № 3. URL: https://repository.tudelft.nl/islandora/object/uuid:4ee188ab-8ce0-4df3-adf5-9010ebfaabf0.
Заглавное фото:
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц
















