Прессиометрические и штамповые испытания лондонской глины. Часть 1. Сравнение методов анализа
 Бершов Алексей Викторовичгенеральный директор ГК «ПЕТРОМОДЕЛИНГ», преподаватель кафедры инженерной геологии Геологического факультета МГУ имени М.В. Ломоносоваalexey.bershov@petromodeling.com
Бершов Алексей Викторовичгенеральный директор ГК «ПЕТРОМОДЕЛИНГ», преподаватель кафедры инженерной геологии Геологического факультета МГУ имени М.В. Ломоносоваalexey.bershov@petromodeling.com
При поддержке ГК «ПетроМоделинг», партнера журнала «ГеоИнфо», редакция начинает знакомство читателей с методами оценки напряженно-деформированного состояния массива грунтов с целью перехода к трехмерному моделированию геологической среды и построению инженерных цифровых моделей геологической среды как базовой части информационной цифровой модели объекта капитального строительства, без которой любые информационные проектные построения просто «повисают в воздухе».
Начнем с рассмотрения прессиометрических испытаний грунтов, которые на сегодняшний день большинством изыскателей и проектировщиков воспринимаются как «более дешевая и простая альтернатива штамповых испытаний». На деле данная технология является уникальным методом испытаний грунтов в массиве. Она используется для определения как действующих горизонтальных напряжений и коэффициента К0 (без которого, как известно, невозможны оценка начального (природного) состояния геологической среды и дальнейшие расчетные обоснования конструкций), так и физико-механических откликов геологической среды на горизонтальное механическое воздействие. Например, таких как зависимость между напряжениями и деформациями и недренированная прочность.
В первых двух публикациях представлен подробный обзор материалов статьи А. Марслэнда и М.Ф. Рэндольфа (сотрудников Научно-исследовательского института по строительству Департамента по вопросам окружающей среды Великобритании) «Сравнение результатов прессиометрических испытаний и крупномасштабных полевых штамповых испытаний лондонской глины» [1]. Эта большая работа была опубликована в журнале Geotechnique («Геотехника») еще в 1977 году, но до сих пор представляет интерес для инженеров-геологов, использующих в своих исследованиях прессиометрические и штамповые испытания грунтов.
Здесь будет представлена первая часть обзора, в которой рассматриваются и сравниваются некоторые методы анализа результатов полевых прессиометрических и штамповых испытаний, предложенные другими исследователями до 1977 года.
Оригинальная статья разделена на две части, поэтому и данный обзор будет состоять из двух частей.
ВВЕДЕНИЕ
Свою статью «Сравнение результатов прессиометрических испытаний и крупномасштабных полевых штамповых испытаний лондонской глины» [1], опубликованную в журнале Geotechnique («Геотехника») в 1977 году, А. Марслэнд и М.Ф. Рэндольф начинают с небольшого обзора по истории возникновения и развития методов прессиометрических испытаний грунтов в скважинах и соответствующих приборов – прессиометров. В итоге они отмечают, что к настоящему времени разработаны достаточно общие методы анализа, которые позволяют непосредственно по данным прессиометрических испытаний получать кривые «напряжение – деформация».
Далее Марслэнд и Рэндольф кратко рассказывают об испытаниях именно лондонской глины другими исследователями и на основе этого делают вывод, что на измеренные значения прочности на сдвиг может серьезно повлиять соотношение размеров исследуемого объема грунта и размеров неповрежденных блоков между трещинами. Поэтому эмпирические корреляции, основанные на сравнениях между данными мелкомасштабных полевых тестов (таких как испытания прессиометром, крыльчаткой и коническим пенетрометром) и лабораторных испытаний небольших образцов, могут быть обманчивыми, если не принимать во внимание возможное влияние масштаба.
В первой части статьи [1] представлены различные методы анализа полевых штамповых и прессиометрических испытаний в попытке найти единый согласованный способ интерпретации их результатов.
ПОЛУЧЕНИЕ ПАРАМЕТРОВ ГРУНТА ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ ПЛОСКИМИ ШТАМПАМИ
Как указывают авторы статьи [1], плоские штампы для полевых тестов обычно являются достаточно жесткими. При анализе результатов таких испытаний обычно принимается, что зависимость напряжений от деформаций грунта подчиняется идеально-упругопластическому закону. Ссылаясь на других авторов, Марслэнд и Рэндольф [1] приводят следующий обзор.
Модуль сдвига
Одна из предложенных формул для осадки жесткого нагруженного штампа на поверхности упругого полупространства выглядит так:

где p – осадка штампа; P – общая нагрузка, приложенная к нему; B – диаметр штампа; E – модуль упругости (Юнга) полупространства; G – модуль сдвига полупространства, G=E/[2(1+ν)]; ν – коэффициент Пуассона.
Далее авторы статьи [1] указывают, что для осадки штампа на дне необсаженной скважины необходимо использовать коэффициент, связанный с глубиной:

где q – среднее давление на штамп, q=P/(πB2/4); f(z) – коэффициент глубины, равный отношению осадки нагруженного штампа на глубине z к осадке нагруженного штампа на поверхности (для недренированных испытаний при ν=0,5 на глубине, превышающей диаметр штампа в 6 раз, этот коэффициент составляет около 0,85).
Отсюда модуль сдвига может быть рассчитан по результатам штампового испытания следующим образом:

Марслэнд и Рэндольф [1] подчеркивают, что формула (3) может быть строго применима только к линейно-упругому полупространству. На практике же модуль сдвига для материалов с нелинейным поведением (например, дисперсных грунтов) может быть получен путем разумного выбора диапазона давления на основание (q), на котором измеряется осадка штампа. Обычно используют секущие модули в диапазоне напряжений от 0 до 1/3 или до 1/2 от общей предельной несущей способности qu (см. линию OA на рисунке 1). Значения модуля зависят от диапазона напряжений, в которых измеряются осадки, из-за изогнутости графиков «нагрузка – осадка».
![Рис. 1. Типичные кривые «нагрузка – осадка» по результатам испытаний штампом диаметром 865 мм [1]](/images/dynamic/img45336.jpg)
По мнению авторов работы [1], разумно сравнить секущие модули, измеренные в одинаковых диапазонах напряжений сдвига при двух указанных типах полевых испытаний. Подходящий диапазон – от напряжений in situ до точки, в которой максимальное напряжение сдвига увеличилось на cu. В идеально-упругопластичном материале это будет точка, в которой начинает развиваться пластическая зона и, следовательно, начинают быстрее увеличиваться деформации.
Далее Марслэнд и Рэндольф [1] напоминают, что нагружение жесткого штампа приводит к немедленному развитию пластических деформаций по его краям. Однако подавляющая часть грунта под штампом останется при гораздо более низких напряжениях сдвига. Ссылаясь на других исследователей, авторы работы [1] пишут о том, что увеличение напряжения сдвига можно оценить по среднему приложенному давлению. Максимальное напряжение сдвига на осевой линии под равномерно нагруженной зоной равно 0,3 от приложенного давления. Под жестким штампом распределение напряжений является более сложным, но указанное соотношение и в этом случае является приблизительно верным. Поэтому приложенное давление q, при котором максимальное напряжение сдвига равно сu, примерно составляет 3,33сu. И здесь, забегая вперед, Марслэнд и Рэндольф [1] указывают, что по данным штамповых испытаний лондонской глины эффективное приложенное давление при разрушении составило (qu–γsz)≈9,6сu, где γsz – общее давление вышележащего грунта.
Из вышесказанного авторы статьи [1] делают вывод, что секущий модуль следует измерять в диапазоне напряжений от γsz до приложенного давления q, причем:
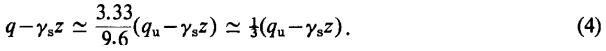
Диапазон напряжений, определяемый этим уравнением, Марслэнд и Рэндольф [1] затем примут как наиболее подходящий для определения секущего модуля сдвига на основе результатов испытаний нагруженным штампом. Они указывают, что значения касательного модуля при давлениях на основание, соответствующих природным давлениям вышележащих грунтов (см. линию DE на рис. 1), также представляют интерес при сравнении с величинами, найденными по данным прессиометрических испытаний.
Прочность на сдвиг в недренированных условиях
Теоретическая зависимость для несущей способности фундамента глубокого заложения в глине такова:

где qu – предельное давление на основание; Nc – теоретический коэффициент несущей способности для конкретного типа фундамента; сu – недренированная прочность на сдвиг; γsz – общее давление вышележащего грунта.
Приблизительные значения Nc для круглого фундамента глубокого заложения могут быть получены на основе модуля сдвига G и недренированной прочности грунта на сдвиг, если рассматривать потерю устойчивости основания фундамента как аналог расширения сферической полости.
Формула для вычисления предельного давления, при котором происходит непрерывное расширение сферической полости в однородном изотропном идеально-упругопластическом материале и в котором не меняется объем, выглядит следующим образом:

где pL – общее предельное давление; G – модуль сдвига грунта, G=Eu/3, где Eu – модуль Юнга, полученный для недренированных условий (при этом Марслэнд и Рэндольф [1] напоминают, что на практике значение модуля сдвига обычно принимается независимым от дренированности или недренированности условий).
Из измененной формулы (6) для расширяющейся сферической полости было выведено уравнение для несущей способности фундамента глубокого заложения с учетом различий в механизмах потери устойчивости для двух случаев:
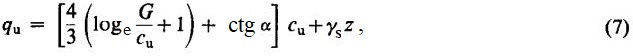
где γsz – общее давление вышележащего грунта; ctg α позволяет учесть напряжение сдвига вдоль границы упругопластической зоны, которая формируется под фундаментом или вдоль поверхности заостренной сваи.
Для плоского основания, нагруженного так, чтобы произошла недренированная потеря устойчивости в глине, α=45 град. и
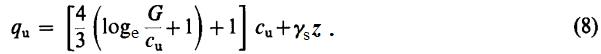
На основе формул (8) и (5) можно получить значения Nc, которые изменяются примерно от 5 для материала с отношением G/cu=7 до 9–10 для материала с отношением G/cu>150. Более высокие значения согласуются с приблизительными величинами Nc для свай, заделанных в идеально-жесткопластическую среду. Для свай с плоским нижним концом: Nc=9,34, если пренебречь влиянием сопротивления основания со стороны сил сдвига, действующих на вертикальные стороны сваи; Nc=9,74, если полностью учесть влияние этих сил сдвига.
Марслэнд и Рэндольф [1] подчеркивают, что уравнение (8) было получено для идеально-упругогопластического материала, поэтому величины G и cu, используемые для нахождения Nc для реального грунта, будут эквивалентными. Например, для деформационно упрочняющегося материала следует использовать значение G, равное секущему модулю сдвига в диапазоне от 0 до 1/2 от предельного напряжения сдвига (рис. 2, а). Для деформационно разупрочняющихся материалов соответствующая прочность cu будет находиться где-то между пиковыми и остаточными значениями (рис. 2, б).
![Рис. 2. Идеализация кривых «напряжение – деформация» для реального грунта с помощью эквивалентной идеально-упругопластической кривой: а – деформационное упрочнение; б – деформационное разупрочнение [1]](/images/dynamic/img45342.jpg)
В случае испытаний с использованием нагружения круглых штампов в скважинах силы сдвига, действующие на вертикальные стороны штампа, невелики и значение Nc=9,34 является подходящим при условии, что штамп имеет тот же диаметр, что и скважина. Это также хорошо согласуется со значениями, полученными в результате модельных испытаний в восстановленной лондонской глине.
В настоящее время, как подчеркивают авторы работы [1], наиболее надежными для ненарушенной лондонской глины являются те значения Nc, которые определяются по предельной несущей способности, измеренной при нагружении штампов диаметром 865 мм на глубине 6,1 м в рассматриваемом месте, и по соответствующим значениям прочности на сдвиг, измеренным при трехосных испытаниях образцов диаметром 98 мм. С глубины 6,1 м были получены ненарушенные образцы диаметром 98 мм, а для измерений прочности при их трехосных испытаниях трещины были достаточно близко расположены, чтобы обеспечить разумные величины, соответствующие таковым при крупномасштабных испытаниях. В результате были получены значения Nc в диапазоне 8,70–9,65 со средним значением 9,25.
Марслэнд и Рэндольф [1] отмечают, что величины Nc на более глубоких уровнях, где изменяется структура глины, могут быть другими. Чтобы получить надежные корреляции для большей глубины, необходимо провести испытания образцов, достаточно крупных для репрезентативного отражения структуры грунта. Но не существует оборудования для получения и испытаний уж очень больших образцов. Из-за отсутствия независимых корреляций для этих глубин авторы работы [1] для получения недренированной прочности на сдвиг по результатам штамповых испытаний будут повсеместно использовать значение Nc=9,25.
ИСПОЛЬЗОВАНИЕ ДАННЫХ ПРЕССИОМЕТРИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ АНАЛИЗА ПОВЕДЕНИЯ ИДЕАЛЬНО-УПРУГОПЛАСТИЧЕСКОГО ГРУНТА
Здесь авторы статьи [1] снова приводят небольшой обзор, ссылаясь на других исследователей. В своей работе [1] Марслэнд и Рэндольф использовали метод анализа, предложенный Джибсоном и Андерсоном (Gibson, Anderson, 1961 году), которые приняли грунт идеально-упругопластическим.
Модуль сдвига
Для случая расширения цилиндрической полости в неограниченной линейно-упругой среде была получена следующая формула:

где G – модуль сдвига; Δp, ΔV – приращение давления и соответствующее изменение объема в упругой области; Vm – средний объем полости в диапазоне приращения давления Δp.
Эта формула записана в инкрементной форме, давая секущий модуль сдвига, который в реальном грунте будет изменяться в зависимости от выбранного диапазона давлений. Для упругого диапазона максимальное напряжение сдвига возникает на краю скважины и равно изменению общего давления. Поэтому пластическая деформация начинается в грунте, прилегающем к зонду, когда увеличение общего давления становится равным cu. Соответствующий секущий модуль (по аналогии с анализом штамповых испытаний) должен измеряться в диапазоне от pо до (pо+cu), где pо – горизонтальное напряжение in situ.
Прочность на сдвиг в недренированных условиях
Была получена следующая формула для общего предельного давления, необходимого для расширения бесконечно длинной цилиндрической полости:
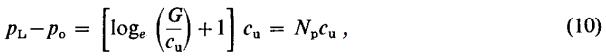
где pо – исходное общее горизонтальное напряжение в грунте; Np=[loge(G/cu)+1] – прессиометрическая постоянная (это выражение аналогично Nc в формуле (5)).
Уравнение (10) может быть использовано для оценки сдвиговой прочности cu при условии, что могут быть определены приемлемые значения pL, pо и Np.
Поскольку модуль сдвига G измеряется на ранней стадии прессиометрического испытания, величина Np может быть определена с использованием последовательных оценок cu в формуле для Np до тех пор, пока не будет получен приемлемый результат, то есть пока оцененная величина cu не будет соответствовать значению, вычисленному по формуле cu=(pL–ро)/Np. Однако против этого метода есть следующее возражение: измеренный модуль сдвига, вероятно, будет ниже, чем его истинное значение in situ, из-за разупрочнения грунта во время бурения скважины. Как и при анализе результатов штамповых испытаний, отношение G/cu в формуле для Np относится к общим эквивалентным значениям модуля сдвига и прочности на сдвиг в ненарушенном грунте.
Марслэнд и Рэндольф [1] отмечают, что формулы для Nc и Np похожи между собой, а это дает хороший метод для оценки прочности грунта на сдвиг по результатам штамповых и прессиометрических испытаний. Из уравнений (5), (8) и (10) можно получить:
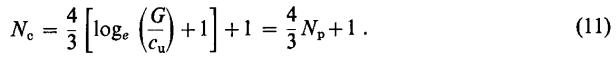
Отсюда:

Это дает значения Np от 6 до 6,75, в то время как Nс изменяется от 9 до 10 для Nс=9,25 и Np=6,18.
Авторы работы [1] подчеркивают, что главные допущения, касающиеся двух рассматриваемых типов испытаний, заключаются в том, что в обоих случаях деформируется достаточный объем грунта, чтобы преодолеть влияние структуры глины, и в том, что отношение G/cu не зависит от анизотропности глины.
ИСПОЛЬЗОВАНИЕ ДАННЫХ ПРЕССИОМЕТРИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ АНАЛИЗА ПОВЕДЕНИЯ ОДНОРОДНОГО НЕСЖИМАЕМОГО ГРУНТА ПРИ ЕГО ОСЕСИММЕТРИЧНОМ ДЕФОРМИРОВАНИИ ПОД ПРЯМЫМ УГЛОМ К ОСИ СКВАЖИНЫ
Здесь авторы статьи [1] опять приводят небольшой обзор, ссылаясь на других авторов.
Было разработано несколько похожих между собой методов получения кривых «напряжение – деформация» для глин по кривым «давление – объем», полученным на основе прессиометрических испытаний. В своей работе [1] Марслэнд и Рэндольф использовали метод анализа по Пальмеру (Palmer, 1972) со следующими допущениями: нагружение вызывает осесимметричную деформацию в плоскости, перпендикулярной оси скважины; грунт является однородным и несжимаемым (последнее подразумевает, что грунт полностью водонасыщен и во время испытания нет дренажа).
Напряжение сдвига τ в грунте рядом со стенкой расширяющейся скважины определяется по формуле:

где y1 – относительное радиальное расширение скважины, равное отношению увеличения ее радиуса из-за роста давления на (p–po) к ее радиусу в исходном состоянии при p=po; dp/dy – градиент давления.
Здесь авторы работы [1] отмечают, что величина y1 численно равна тангенциальной деформации εθ на краю скважины, но имеет противоположный знак (поскольку деформации сжатия принимаются как положительные).
Условия несжимаемости и плоской деформации подразумевают следующее:

Таким образом:

Максимальная деформация сдвига на краю ствола скважины определяется по формуле:

Модуль сдвига
Для материалов, обладающих нелинейным поведением, математическим определением модуля сдвига является тангенс кривой «напряжение сдвига – сдвиговая деформация» в начале координат, то есть:

где τ – напряжение сдвига; γ – сдвиговая деформация.
Для случая расширения цилиндрической полости при малых деформациях изменение напряжения сдвига в грунте, примыкающем к зонду, составляет Δτ≈Δp, а соответствующая сдвиговая деформация составляет γ≈2y1. Подстановка в уравнение (17) выражения для касательного модуля упругости для исхоного состояния, когда р=ро, дает следующую формулу:

При малых деформациях, поскольку в этом случае y1≈½(ΔV/V0), значения касательного модуля, полученные по формулам (9) и (18), одинаковы.
Марслэнд и Рэндольф [1] напоминают, что для инженерных целей лучше всего подходит секущий модуль. Чтобы его получить, формулу (18) можно переделать следующим образом:

Здесь авторы работы [1] подчеркивают, что, как и в предыдущем анализе, подходящий диапазон напряжений для определения секущего модуля – от р=ро до р=(ро+cu) (где cu – недренированная прочность на сдвиг, полученная в результате уже этого анализа).
Прочность на сдвиг
При малых деформациях уравнение (13) для напряжения сдвига τ можно приблизительно аппроксимировать так:

что приводит к простому геометрическому методу расчета напряжения сдвига непосредственно по кривой «p – y1»
При более сильных деформациях точнее выразить напряжение сдвига следующим образом:

где ΔV – увеличение объема от исходного состояния до текущего объема V рабочей камеры (измерительной ячейки) прессиометра при измеренном давлении.
Это напряжение сдвига, определяемое по наклону кривой «р – loge(ΔV/V)». Максимальный наклон данного графика дает максимальное напряжение сдвига (пиковую сдвиговую прочность грунта). Дифференцируя эту кривую в ряде точек, можно получить график «напряжение сдвига – сдвиговая деформация». Здесь Марслэнд и Рэндольф [1] подчеркивают, что этот метод оценки сu предсказывает максимальные значения прочности на сдвиг, которые достигаются при низких сдвиговых деформациях (например, менее 5% для лондонской глины), в то время как идеально-упругопластический анализ выводит определение прочности на сдвиг из предельного давления, которое теоретически достигается только при неограниченной деформации.
На практике, как отмечают авторы статьи [1], вокруг расширенной камеры прессиометра могут происходить сдвиговые деформации величиной более 30%, а предельное давление соответствует мобилизованной прочности, которая, в свою очередь, соответствует сдвиговым деформациям до указанного значения.
СРАВНЕНИЕ ДВУХ МЕТОДОВ АНАЛИЗА РЕЗУЛЬТАТОВ ПРЕССИОМЕТРИЧЕСКИХ ИСПЫТАНИЙ
Итак, Марслэнд и Рэндольф [1] рассмотрели два основных метода анализа результатов прессиометрических испытаний: для идеально-упругопластического грунта и для однородного несжимаемого грунта при его осесимметричном деформировании под прямым углом к оси скважины. Далее они перечисляют сходства и различия этих методов.
1. Оба рассмотренных метода требуют оценки горизонтального напряжения in situ рo (это напряжение является исходным, относительно которого измеряются все последующие приращения давления).
2. Оба метода предсказывают один и тот же модуль сдвига (либо касательный при pо, либо секущий в диапазоне от pо до (pо+cu)) по заданному набору данных.
3. Идеально-упругопластический анализ, предложенный Джибсоном и Андерсоном (Gibson, Anderson) в 1961 году, дает единственное эквивалентное значение cu, которое при отсутствии влияния масштаба или анизотропии должно быть сопоставимо с величиной, полученной в результате анализа данных штамповых испытаний (этот анализ может особенно хорошо подходить для проектирования фундаментов).
4. Более общий анализ с меньшим количеством ограничений, предложенный Пальмером (Palmer) в 1972 году для однородного несжимаемого грунта при его осесимметричном деформировании под прямым углом к оси скважины, дает полную кривую «напряжение – деформация», где пиковое напряжение сдвига cu прогнозируется при значениях деформации сдвига менее 5%.
ОЦЕНКА ГОРИЗОНТАЛЬНОГО НАПРЯЖЕНИЯ IN SITU ПО РЕЗУЛЬТАТАМ ПРЕССИОМЕТРИЧЕСКИХ ИСПЫТАНИЙ
Марслэнд и Рэндольф [1] подчеркивают, что оба рассмотренных выше типа анализа результатов стандартных прессиометрических испытаний требуют для расчета характеристик грунта точной оценки горизонтального напряжения in situ (pо) – одного из важных параметров для проектирования свай и выемок. На рисунке 3 показан типичный график «давление – объем», построенный на основе испытаний с помощью прессиометра, а также соответствующая кривая ползучести, отражающая изменения объема между 30 секундами и 2 минутами после приложения приращения давления для каждого давления.
![Рис. 3. Типичная кривая «давление p – объем V», построенная на основе испытаний прессиометром на глубине 13,1 м в скважине 2 [1]](/images/dynamic/img45356.jpg)
Авторы статьи [1] напоминают, что стандартный способ оценки горизонтального напряжения in situ основывается на принятии соответствия величины pо началу линейной области кривой «давление – объем», а также точке на кривой ползучести, начиная с которой ползучесть падает до низкого постоянного значения. Однако, по их мнению, есть основания полагать, что в случае переуплотненного грунта использование этого способа приведет к значительному занижению значения pо.
Марслэндом и Рэндольфом [1] был разработан новый метод, с помощью которого величина pо оценивается по кривой «p – y1» (напомним, что y1 – это относительное радиальное расширение скважины, то есть отношение увеличения ее радиуса из-за роста давления на (p–po) к ее радиусу в исходном состоянии при p=po).
Также может быть полезной кривая «давление p – объем V» (см. рис. 3) с учетом следующих моментов.
1. При идеальном прессиометрическом испытании небольшие положительные или отрицательные приращения давления по отношению к pо должны обеспечить сходные изменения объема.
2. Из первого пункта следует, что значение pо должно лежать на почти прямолинейном участке кривой «p – V», но вблизи изгиба, а не в начале линейной области.
3. Поскольку в идеально-упругопластическом материале увеличение pо на cu вызывает пластическую текучесть в глине рядом с зондом, то должно происходить заметное увеличение кривизны, когда давление превышает значение (pо+cu). Величина cu здесь является пиковой в соответствии с вышеупомянутым анализом по Пальмеру (Palmer, 1972). Поскольку для оценки этой величины должно быть определено значение pо, необходима некоторая итерация, посредством которой производится первоначальная оценка pо. Затем вычисляется cu, а потом выполняется проверка, чтобы определить, соответствует ли полученное значение (pо+cu) давлению, при котором кривая «p – y1» становится существенно нелинейной. Здесь Марслэнд и Рэндольф [1] отмечают, что этот метод использовался только для прессиометрических испытаний в полутвердой глине (для чего он особенно хорошо подходит, поскольку кривая «напряжение – деформация» является достаточно линейной вплоть до пиковых значений прочности). Но для анализа результатов испытаний более слабого грунта перед применением указанного метода необходимы дополнительные корреляции. (Применение данного метода авторы статьи [1] обсуждают во второй, практической, части статьи, обзор материалов которой будет сделан в следующий раз.)
ОЦЕНКА ПРЕДЕЛЬНОГО НАПРЯЖЕНИЯ ПО ДАННЫМ ПРЕССИОМЕТРИЧЕСКИХ ИСПЫТАНИЙ
Марслэнд и Рэндольф [1] напоминают, что после бурения скважины для испытаний прессиометром напряжение уменьшается от pо до γfz, где γf – удельный вес бурового раствора. Ссылаясь на Гибсона и Андерсона (Gibson, Anderson, 1961) они пишут, что если принять этот процесс разгрузки линейным и измерять последующие увеличения давления и объема относительно указанного исходного состояния, то зависимость для давления p на более поздних, пластических, стадиях испытания будет выглядеть так:
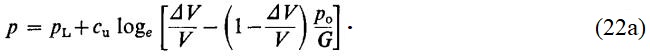
С помощью этой формулы можно оценить сu и pо. Предельное напряжение pL здесь оценивается путем построения графика зависимости давления p от следующей величины:

Однако, как отмечают авторы работы [1], принятие линейной разгрузки от pо до γfz не подтверждается на практике, если типичная кривая повторного нагружения является нелинейной на ранних стадиях (см. рис. 3). Чтобы преодолеть ошибки, вносимые допущением линейности указанной разгрузки, все давления и объемы должны измеряться относительно горизонтального напряжения in situ pо, а соответствующий объем рабочей камеры прессиометра Vо должен считываться с кривой «p – V».
Марслэнд и Рэндольф [1] приводят новую формулу для давления p, которая заменяет уравнение (22а):

где V – общий объем при давлении р; ΔV – изменение объема, равное (V–Vо), где Vо – объем при давлении pо.
Это уравнение подразумевает, что график зависимости p от logе(ΔV/V) должен быть почти линейным для более поздних этапов испытания при условии, что допущение об идеально-упругопластическом материале является разумным. Отсюда следует, что экстраполяция кривой к logе(ΔV/V)=0 (что соответствует непрерывному расширению рабочей камеры прессиометра, поскольку ΔV/V=ΔV/(Vо+ΔV)=1, откуда ΔV=∞) обеспечит хорошую оценку предельного напряжения pL. (Этот процесс Марслэнд и Рэндольф описывают во второй части статьи [1], обзор материалов которой будет представлен в следующий раз.)
-
Результаты испытаний, выполненных в лондонской глине, и их сравнение будут рассмотрены во второй части обзора материалов статьи Марслэнда и Рэндольфа [1]
ИСТОЧНИК ДЛЯ ОБЗОРА
1. Marsland A., Randolph M. F. Comparisons of the results from pressuremeter tests and large in situ plate tests in London Clay // Geotechnique. 1977. Vol. 27. № 2. P. 217–243.
СПИСОК ЛИТЕРАТУРЫ, ИСПОЛЬЗОВАННОЙ АВТОРАМИ СТАТЬИ [1]
Agarwal K.B. The influence of size and orientation on the strength of London Clay: PhD thesis. London, UK: University of London, 1967. (Summarized by Simon N.E. Shear strength of stiff clays // Proc. Conf. Shear Strength Properties of Natural Soils and Rocks. Discussion. Session 2. Oslo, 1967. P. 159–160.)
Amar S., Baguelin F., Jezequel J.F., Le Mehaute A. In situ shear resistance of clays // Proc. conf. In-situ Measurement of Soil Properties. North Carolina State University, 1975. Vol. 1. P. 22–45.
Baguelin F., Jezequel J.F., Lemee E., Le Mehaute A. Expansion of cylindrical probes in cohesive soils // JSMFE. ASCE, 1972. Vol. 98. SMll. P. 1129–1142.
Baguelin F., Jezequel J.F. Discussion // Geotechnique. 1973. Vol. 23. № 2. P. 287–291.
Bishop R.F., Hill R., Mott N.F. The theory of indentation and hardness tests // Proc. Phys. Soc. 1945. Vol. 57. № 3. P. 147–159.
Bishop A.W. The strength of soils as engineering materials // Geotechnique. 1966. Vol. 16. № 2. P. 89–130.
Bishop A.W., Webb D.L., Lewin P.I. Undisturbed samples of London Clay from the Ashford Common Shaft: strength-effective stress relationships // Geotechnique. 1965. Vol. 15. № 1. P. 1–31.
Bishop A.W., Little A.L. The influence of the size and orientation of the sample on the apparent strength of the London Clay at Maldon, Essex // Proc. Conf. Shear Strength Properties of Natural Soils and Rocks. Oslo, 1967. Vol. 1. P. 89–96.
Burland J.B. Contribution to discussion // Proc. Conf. In-situ Investigation in Soils and Rocks. London, UK: British Geotechnical Society, 1969. P. 61–62.
Burland J.B., Butler F.G., Dunican P. The behaviour of large diameter bored piles in London Clay // Proc. Symp. Large Bored Piles. London, UK: Institution of Civil Engineers, 1966. P. 51–71.
Gibson R.E. Correspondence // J. Znstn. Civ. Engrs. 1950. Vol. 34. P. 382–383.
Gibson R.E. The analytical method in soil mechanics // Geotechnique. 1974. Vol. 24. № 2. P. 113–139.
Gibson R.E., Anderson W.F. In situ measurement of soil properties with the pressuremeter // Civ. Engng Publ. Wks Rev. 1961. Vol. 56. № 658. P. 615–618.
Hartman P.J., Schmertmann J.H. FEM study of elastic phase of pressuremeter tests // Proc. Conf. In-Situ Measurement of Soil Properties. North Carolina State University, 1975. Vol. 1. P. 190–207.
Hill R. The mathematical theory of plasticity. Oxford University Press, 1950.
Hobbs N.B., Dixon J.C. In-situ testing for bridge foundation in the Devonian Marl // Proc. Conf. In-situ Investigations in Soils and Rocks. 1970. Vol. 4. P. 31–38.
Ladanyi B. Expansion of a cavity in a saturated clay medium // J. Soil Mech. Fdn Engng. Am. Soc. Civ. Engrs., 1963. Vol. 89. SM4. P. 127–161.
Ladanyi B. In-situ determination of undrained stress-strain behaviour of sensitive clays with the pressuremeter // Canad. Geotech. J. 1972. Vol. 9. № 3. P. 313–319.
Marsland A. Discussion // Proc. 5th Int. Conf. Soil Mech. Fdn Engng. 1961. Vol. 3. P. 179–180.
Marsland A. Discussion // Conf. Shear Strength Properties of Natural Soils and Rocks. Session 2. Oslo, 1967. Vol. 2. P. 160–161.
Marsland A. The shear strength of stiff fissured clays // Proc. Roscoe Memorial Symp. Stress-strain behaviour of Soils. Foulis, 1971. P. 59–68.
Marsland A. Large in-situ tests to measure the properties of stiff fissured clays // Proc. 1st Australian – New Zealand Conf. Geotechnics. Melbourne, 1971. Vol. 1. P. 180–189.
Marsland A. Laboratory and in-situ measurements of the deformation moduli of London Clay // Proc. Symp. Interaction of Structure and Foundation. University of Birmingham, July 1971. P. 7–17. (Also BRE Current Paper CP24/73.)
Marsland A. Model studies of deep in-situ loading tests in clay // Civ. Engng Publ. Wks Rev. 1972. Vol. 67. № 792. P. 695, 697–698.
Marsland A. Comparison of the results of static penetration tests and large in-situ plate tests in London Clay // Proc. European Symp. Penetration Testing. Stockholm, 1974. P. 212, 245–252.
McKinlay D.G., Anderson W.F. Glacial till testing and an improved pressuremeter // Civ. Engng. 1974. P. 47–53.
Meigh A.C., Greenland S.W. In-situ testing of soft rocks // Proc. 6th Int. Conf. Soil Mech. Fdn Engng. 1965. Vol. 1. P. 73–76.
Menard L.F. Mesures in situ des proprietes physiques des soils // Annales des Ponts et Chaussees. 1957. Vol. 127. № 3. P. 357–377.
Menard L.F. Calcul de la force portante des fondations sur la base des resultats des essais pressiometriques // Sols-Soils. 1963. Vol. 2. № 5, 6. P. 9–28.
Menard L.F. Rules for the calculation of bearing capacity and foundation settlement based on pressuremeter tests // Proc. 6th Int. Conf. Soil Mech. Fdn Engng. 1965. Vol. 2. P. 295–299 (in French).
Menard L.F. The interpretation and application of pressuremeter tests results // Sols-Soils. 1975. № 26.
Meyerhoff G.G. The ultimate bearing capacity of foundations // Geotechnique. 1951. Vol. 2. № 4. P. 312–316.
Meyerhoff G.G. The ultimate bearing capacify of wedge-shaped foundations // Proc. 5th Int. Conf. Soil Mech. Fdn Engng. Paris, 1961. Vol. 2. P. 105–109.
Palmer A.C. Undrained expansion of cylindrical cavity in clay // Geotechnique. 1972. Vol. 22. № 3. P. 451–457.
Poulos H.G., Davis E.H. Elastic solutions for soil and rock mechanics. New York: Wiley, 1973.
Skempton A.W. Horizontal stresses in an overconsolidated Eocene clay // Proc. 5th Int. Conf. Soil Mech. Fdn Engng. Paris, 1961. Vol. 1. P. 351–357.
Skempton A.W., La Rochelle P. The Bradwell Slip: a short term failure in London Clay // Geotechnique. 1965. Vol. 15. № 3. P. 221–242.
Terzaghi K. Theoretical soil mechanics. New York: Wiley, 1943.
Timoshenko S.P., Goodier J.N. Theory of elasticity. New York: McGraw Hill, 1951.
Windle D., Wroth C.P. In-situ measurement of the properties of stiff clays // Proc. 9th Int. Conf. Soil Mech. Fdn Engng. Tokyo, 1977.
Wroth C.P., Hughes J.M.O. An instrument for the in-situ measurement of the properties of soft clays // Proc. 8th Int. Conf. Soil Mech. Fdn Engng. Moscow, 1973. Vol. 1. P. 487–494.
Wroth C.P., Hughes J.M.O. Discussion // Geotechnique. 1973. Vol. 23. № 2. P. 284–287.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц

















