Заметки Питера Вермеера. Метод конечных элементов (МКЭ) для анализа взаимодействия подпорной стенки и грунта

Основатель программного комплекса PLAXIS Питер Вермеер посвятил свою колонку в десятом номере журнала Plaxis Bulletin [5] численному анализу взаимодействия между грунтом и ограждением котлована с одним уровнем распорного или анкерного крепления.

Он напомнил читателям, что анализ гибких (шпунтовых) подпорных стенок стал возможным благодаря работам Германа Блюма (Hermann Blum), опубликованным в 1930-х годах (речь идет исключительно о зарубежной практике. — Ред.). В этих работах различалось два типа шпунтовых стенок, заанкеренных или подпертых подкосами только на одном уровне, — с фиксированным и нефиксированным положением нижнего торца (соответственно, с достаточным и недостаточным заглублением). Согласно определению Блюма полная фиксация подошвы такой стенки достигается тогда, когда моменты сдвигающих и опрокидывающих сил становятся равны моментам удерживающих сил. Сегодня методы расчетов Блюма для стенок с фиксированным и нефиксированным положением нижнего торца (соответственно, fixed earth support method и free earth support method) можно найти в большинстве учебников.

По мнению Вермеера, указанные работы Блюма внесли колоссальный вклад в механику грунтов, однако предлагаемые в них методы анализа являются упрощенными и не учитывают ни жесткость стенок, ни жесткость грунта, а значит, результаты их использования неизбежно будут неточными. Поэтому в настоящее время (на момент написания колонки в 2001 г. — Ред.) в основном используются модели грунтового основания «пружинного» типа на основе классической расчетной модели Винклера (которая с физической точки зрения может быть представлена множеством не связанных друг с другом одинаковых упругих пружин, опирающихся на абсолютно жесткое основание (рис. 1) [4]. — Ред.).

Рис. 1. Физическое представление модели грунтового основания по Винклеру [4]

К сожалению, трудно выбрать соответствующие «пружинные» постоянные (коэффициенты постели), поэтому для оценки роли жесткости грунта и ограждения котлована Вермеер предпочел использовать метод конечных элементов (МКЭ). Для этого он проанализировал поведение подпорной стенки борта котлована с распорками только на одном уровне для трех разных случаев (в таблице — соответственно А, Б, В):

1) «гибкая (шпунтовая) стенка — жесткий грунт»;

2) «жесткая “стена в грунте” — жесткий грунт»;

3) «жесткая “стена в грунте” — слабый грунт»

Таблица. Параметры жесткости подпорной стенки и грунта для трех рассмотренных случаев

Вермеер рассмотрел три указанных случая с одинаковыми геометрическими параметрами:

• глубина котлована 10 м;
• заглубление подпорной стены ниже дна котлована 2,5 м;
• уровень распорного (или анкерного) крепления — на глубине 2,5 м от дневной поверхности.

Сила, имитирующая распорное (или анкерное) крепление в верхней части, была задана равной 100 кН/м (рис. 2).

Рис. 2. Три стадии создания ограждения котлована с распорками на одном уровне: 1 — первая выемка грунта; 2 — установка распорки (на практике — чуть выше уровня грунтовых вод); 3 — окончательная выемка грунта [5]

Для всех трех случаев были приняты следующие свойства грунта:

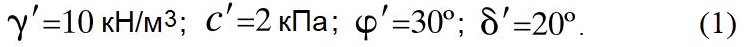
При этом Вермеер отметил, что использовался удельный вес водонасыщенного грунта, так как рассматривался уровень грунтовых вод на поверхности грунта, который не снижался ни с одной из сторон подпорной стенки.

Было принято, что выемка грунта проводилась в три этапа (см. рис. 2):

1) создание ограждающей конструкции и выемка грунта из будущего котлована до глубины 2,5 м;

2) приложение нагрузки 100 кН/м, имитирующей воздействие распорки;

3) выемка грунта до окончательной глубины котлована.

Поведение грунта моделировалось с использованием модели упрочняющегося грунта (HS) в программном комплексе PLAXIS. Для первичного нагружения при испытаниях в одометре это означает увеличение модуля деформации по следующей формуле:

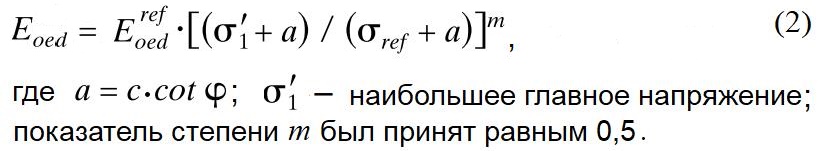
(Выполнять подобные расчеты с помощью модели Мора — Кулона нельзя, поскольку в ней задается только один модуль (как правило, модуль деформации), а модуль упругости при разгрузке автоматически приравнивается, что приводит к чрезмерному подъему дна котлована и полному искажению картины деформаций и усилий. — Ред.)

В рамках модели HS разгрузка и повторное нагружение описываются на основе закона Гука. Модуль упругости для разгрузки и повторного нагружения для приращений напряжения и деформации определяется формулой:

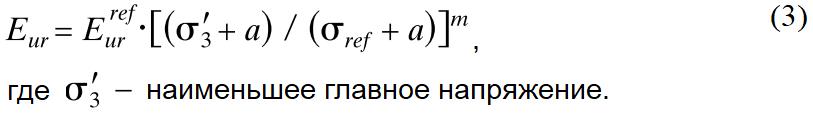
Для всех вариантов коэффициент переуплотнения OCR был принят равным 1,0, а начальные напряжения были рассчитаны с использованием K₀ = 0,5.

Модель HS также использует в качестве входного параметра жесткость грунта при стандартных трехосных испытаниях в дренированных условиях (Е₅₀ — Ред.). (Изменение сдвиговой жесткости учитывается моделью так же, как в формулах (2) и (3). — Ред.)

Для всех вариантов были использованы следующие соотношения:

Вермеер отметил, что единственная разница между жестким грунтом случаев A, Б и слабым грунтом в случае В (см. таблицу) связана с модулями деформации. Жесткий грунт имеет модуль деформации в 15 раз больше, чем слабый, но и для того, и для другого сохраняется следующее соотношение:

Кроме того, как добавил автор колонки, и для жесткого, и для слабого грунта удобно задавать одинаковые параметры прочности.

Случай А (рис. 3, а)

На рисунке 3 (а) показаны результаты выполненного Вермеером численного анализа комбинации жесткого грунта и гибкой (шпунтовой) подпорной стенки с распорками на уровне (глубине) 2,5 м от дневной поверхности. Здесь можно увидеть значительный изгиб стенки до величины около 5 см. Как следствие, значительно уменьшается активное давление грунта — даже ниже «классического минимума» величины e_ah (что возможно только при численном расчете — Ред.). Эпюра изгибающих моментов показала максимум между креплением стенки и областью пассивного давления грунта ниже дна котлована.

Рис. 3. Поведение подпорной стенки борта котлована с распорным креплением на одном уровне и нефиксированным положением нижнего конца (при заглублении нижнего конца ограждения на 2,5 м ниже дна котлована) для случаев А, Б и В (см. таблицу)

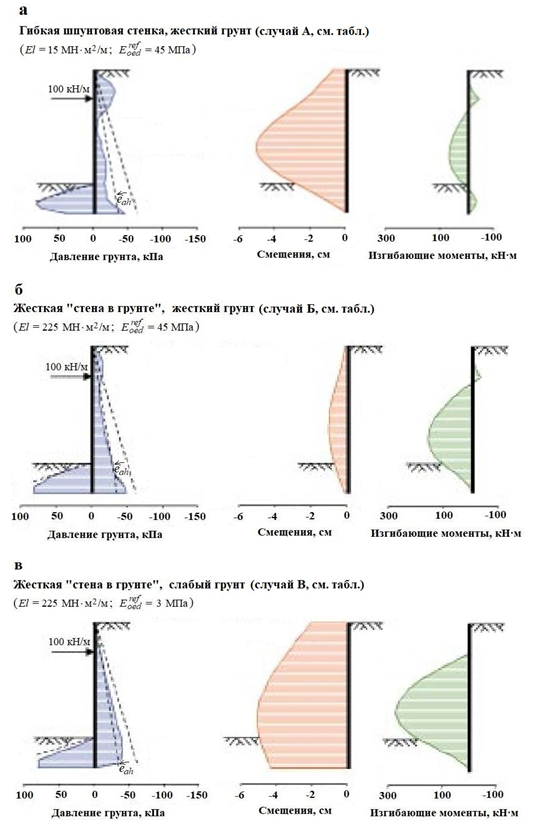
Вермеер отметил, что особенности работы гибких ограждений делает МКЭ предпочтительным для моделирования реакции грунтового основания. Аналитические расчеты с использованием коэффициентов постели приведут к тому, что «пружина» сработает пластически, т.е. активное давление никогда не достигнет значений, меньших чем

На рисунке 2 (а) показано давление для гибких подпорных стенок в жестких грунтах. Видно, что эпюра вычисленного активного давления грунта ниже штриховой линии для значения e_ah, определенного по формуле (6).

Еще одной особенностью стенки с малой жесткостью является заглубление ниже дна котлована, что увеличивает удерживающие силы. Но здесь Вермеер отметил, что заглубление нижнего торца стенки он принял, используя правила расчетов Блюма для стены с нефиксированным положением ее подошвы. При этом расчетные изгибающие моменты из-за знакопеременности и защемления нижнего торца оказались небольшими и составили примерно половину от тех изгибающих моментов, которые следовали бы из правила расчетов Блюма.

Случай Б (рис. 3, б)

Типичные результаты типа итогов расчета по Блюму получились у Вермеера при рассмотрении жесткой подпорной стенки («стены в грунте») в жестком грунте (рис. 3, б). Ниже уровня крепления достигаются классические активные давления грунта. Пассивные давления не полностью мобилизованы, так как Вермеер делал расчеты для стенки с коэффициентом надежности 1,5 по пассивному давлению грунта. Нижний конец ограждения не смещается, а изгибающие моменты хорошо согласуются с изгибающими моментами, которые получаются при использовании методики расчетов Блюма.

Интересно, что, как обращает внимание автор колонки, такие же давления грунта и изгибающие моменты были бы получены для комбинации слабого грунта и гибкой подпорной стенки (такой случай отдельно не рассматривался. — Ред.). Ведь относительная жесткость стенки тогда была бы такой же, как и для случая Б (жесткой подпорной стены в жестком грунте).

Случай В (рис. 3, в)

При рассмотрении Вермеером результатов расчетов для случая В, то есть для жесткой стенки в слабом грунте (рис. 3, в), интересным оказался тот факт, что, несмотря на использование коэффициента надежности 1,5, пассивное давление грунта было почти полностью мобилизовано — вероятно, благодаря увеличенному активному давлению. Очевидно, грунт является настолько деформируемым, что максимального смещения стенки в месте изгиба примерно на 5 см недостаточно для надлежащего снижения давления на активной стороне. Вследствие высокого давления возникает изгибающий момент около 300 кН*м/м, а это далеко за пределами значений, которые получались бы при использовании методики расчетов Блюма.

Для жесткой стенки в слабом грунте Вермеер выразил сомнение в результатах аналитических расчетов с использованием коэффициентов постели, поскольку весьма сложно выбрать правильные значения «пружинных» постоянных, которые потребовались бы как для активной, так и для пассивной зон (в противном случае невозможно предсказать высокие изгибающие моменты, полученные для случая В).

Влияние заглубления нижнего конца подпорной стенки

Для изучения влияния заглубления Вермеер снова обратился к варианту, представленному на рисунке 2, но с заглублением нижнего конца подпорной стенки на 5 м ниже дна котлована (вместо 2,5 м).

В этом случае, если следовать правилам расчетов Блюма, получится полностью защемленное положения нижнего конца стены (момент удерживающих сил будет равен моменту сдвигающих и опрокидывающих сил).

Результаты расчетов для тех же случаев А, Б и В (см. таблицу) показаны на рисунке 4. Для сравнения предыдущие данные для менее заглубленной стенки (см. рис. 3) показаны на рисунке 4 штриховыми линиями.

Рис. 4. Поведение подпорной стенки борта котлована с распорным креплением на одном уровне и фиксированным положением нижнего конца (при заглублении нижнего конца ограждения на 5 м ниже дна котлована) для случаев А, Б и В (см. таблицу). Штриховые линии показывают результаты для глубины заложения нижнего конца ограждения на 2,5 м ниже дна котлована, то есть для его не полностью защемленного положения (см. рис. 3)

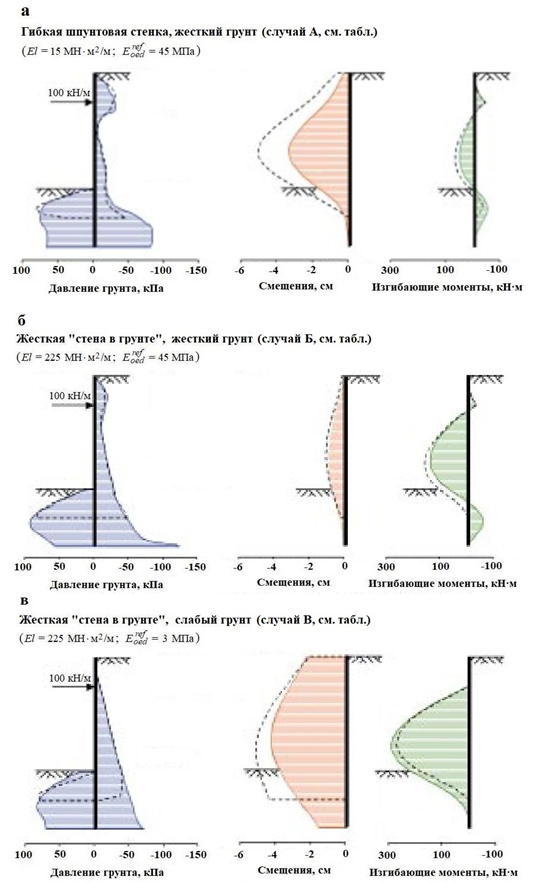
Из рисунка 4 видно, что изгибающие моменты лишь незначительно уменьшаются при увеличении заглубления нижнего конца подпорной стенки. Уменьшение момента сдвигающих и опрокидывающих сил, обусловленное увеличением момента удерживающих сил, более или менее компенсируется небольшим увеличением активного давления, которое вызвано повышением жесткости всей системы.

Здесь Вермеер с удивлением отмечает, что некоторые руководства предполагают значительное влияние заглубления стенок на изгибающие моменты (что приводит к расхождениям между аналитическими и численными результатами. — Ред.).

Что касается перемещений подпорной стенки, то увеличение заглубления привело к их значительному снижению только в случае А (см. рис. 4, а), а в случаях Б и В его влияние не особенно сказалось (см. рис. 4, б, в).

Выводы

На основе полученных им данных Питер Вермеер [5] сделал следующие основные выводы.

При анализе поведения жесткой подпорной стенки («стены в грунте») в жестком грунте (случай Б, см. табл.) получаются примерно такие же результаты, как и при использовании аналитической методики расчетов Блюма. В этом случае будут иметь место классические активные давления грунта, по крайней мере ниже уровня крепления стенки.

Гибкая (шпунтовая) подпорная стенка в жестком грунте (случай А, см. табл.) получит значительные деформации при невысоких изгибающих моментах. Жесткий грунт передаст значительную часть активного давления на изгиб, а в гибкой стенке возникнут небольшие усилия.

Жесткая подпорная стенка («стена в грунте») в слабом грунте (случай В, см. табл.) будет испытывать высокие активные давления и, как следствие, иметь высокие изгибающие моменты.

За счет увеличения заглубления подпорной стенки ниже дна котлована изгибающие моменты, как правило, уменьшаются незначительно.

Источники

1. Заметки Питера Вермеера. Как не игнорировать ползучесть грунтов в геотехнической практике? // Geoinfo.ru. 09.12.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/zametki-pitera-vermeera-kak-ne-ignorirovat-polzuchest-gruntov-v-geotekhnicheskoj-praktike-41820.shtml.
2. Заметки Питера Вермеера. Когда нужен «дренированный» и «недренированный» анализ поведения грунтов? // Geoinfo.ru. 18.11.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/zametki-pitera-vermeera-kogda-nuzhen-drenirovannyj-i-nedrenirovannyj-analiz-povedeniya-gruntov-41720.shtml.
3. Заметки Питера Вермеера. О деформационных параметрах моделей грунта и коэффициенте переуплотнения // Geoinfo.ru. 03.02.2020. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/zametki-pitera-vermeera-o-deformacionnyh-parametrah-modelej-grunta-i-koehfficiente-pereuplotneniya-42125.shtml.
4. docs.cntd.ru/document/420383019.
5. Vermeer P. Column Vermeer // Plaxis Bulletin. 2001. № 10. URL: plaxis.com/content/uploads/2016/10/Plaxis-Bulletin-10.pdf.

Рисунок на заставке: plaxis.com/content/uploads/2016/10/Plaxis-Bulletin-10.pdf.