Заметки Питера Вермеера. Одометрическая жесткость и индекс компрессии слабых грунтов как входные параметры для PLAXIS

В начале своей колонки в 12-м выпуске журнала Plaxis Bulletin (2002 г.) [5] Питер Вермеер напоминает, что для сжатия нормально уплотненных глинистых грунтов используется логарифмический закон:

Однако Терцаги и другие основоположники механики грунтов, предложившие и использовавшие этот закон, жили в докомпьютерные времена, когда графики строились вручную на бумаге с нанесенной на нее десятичной логарифмической сеткой. Но в наше время выведенные ими формулы приходится модифицировать для возможности их удобного использования в компьютерных программах. Следовательно, как указывает Вермеер [5], надо переходить от десятичных логарифмов к натуральным. В этом случае переформулированный логарифмический закон сжатия нормально уплотненных грунтов будет выглядеть следующим образом:

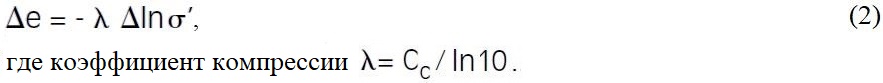
Поскольку вместо коэффициента пористости удобно использовать деформацию, можно получить следующую формулу для этого закона:

Далее в своей заметке [5] Вермеер использует индекс компрессии C_с, модифицированный коэффициент компрессии λ^* и модуль деформации E_oed, полученный по результатам испытаний в одометре.

Автор колонки [5] приводит одну из самых известных геотехнических корреляций (о которой подробнее предлагает узнать в книге Терцаги и Пека [6]):

Он также приводит корреляцию, предложенную Ротом и Вудом [7]:

Несмотря на кажущуюся разницу, корреляции (4) и (5) с точки зрения Вермеера [5] практически идентичны, так как число пластичности обычно можно аппроксимировать следующим образом:

Действительно, для нормально уплотненных грунтов, за исключением пылеватых песков, точки корреляционной зависимости «I_p – W_L» располагаются примерно на прямой линии, параллельной так называемой линии А диаграммы пластичности Казагранде (рис. 1).

Рис. 1. Пределы Аттерберга для двадцать одного образца грунтов, испытанных Энгелем [8]

При использовании формулы (6) корреляция Терцаги и Пека (4) будет выглядеть так:

что очень близко к формуле Рота и Вуда (5).

Учитывая большое количество доказательств в пользу корреляций (5) и (6), Вермеер пришел к выводу, что можно использовать и ту, и другую. Соответственно, можно применять обе следующие формулы:

Последняя лишь незначительно отличается от корреляции (4). По мнению Вермеера, она даже немного лучше.

Далее автор заметки [5] обращается к взаимосвязи между модифицированным коэффициентом компрессии λ^* и индексом компрессии C_с:

Эта аппроксимация получается для коэффициента пористости e, примерно равного единице. Если говорить в общем, то допущение e ≈ 1 является грубым, но оно работает в контексте корреляций для слабых грунтов.

В сочетании с приведенными выше корреляциями для C_с зависимость (10) приводит к следующим формулам:

Для прямой оценки корреляций (11) и (12) Вермеер [5] рассматривает экспериментальные данные Энгеля [8] – модифицированные коэффициенты компрессии λ^* для двадцать одного образца различных глин и пылеватых грунтов с пределами текучести в диапазоне от 0,2 до 1,1 и числами пластичности от 0,03 до 0,70 (см. рис. 1, рис. 2, 3).

Рис. 2. Корреляционная зависимость между модифицированным коэффициентом компрессии λ* и числом пластичности Ip по результатам измерений Энгеля [8]

Рис. 3. Хорошая корреляция между модифицированным коэффициентом компрессии λ* и пределом текучести W_L по результатам измерений Энгеля [8]

Из рисунка 2 можно сделать вывод, что корреляция (11) имеет некоторые недостатки. Тщательная проверка показывает, что она хороша для глин с числами пластичности I_p выше линии А на графике пластичности Казагранде (см. рис. 1), но не для пылеватых грунтов со значениями I_p ниже этой линии.

Чтобы включить в корреляционную зависимость и свойства пылеватых грунтов, лучше было бы использовать формулу (12), как это продемонстрировано на рис. 3. Из графика связи модифицированного коэффициента компрессии λ^* и предела текучести W_L (см. рис. 3) видно, что между ними имеется чрезвычайно хорошая корреляция. Здесь Вермеер [5] напоминает, что корреляция (12) не только подтверждается данными Энгеля [8], но и полностью соответствует результатам работ по корреляциям для C_с, полученным Ротом и Вудом [7], а также Терцаги и Пеком [6]

Далее Вермеер [5] переходит к рассмотрению жесткости слабого грунта по результатам испытаний в одометре. С этой целью он записывает логарифмический закон сжатия (3) в дифференциальной форме:

Таким образом, касательная жесткость по результатам сжатия в одометре, также называемая одометрическим модулем деформации, пропорциональна напряжению. Следовательно:

Эта линейная зависимость жесткости грунта от напряжения хороша для нормально уплотненных глинистых грунтов, но не для песчаных. Поэтому Оде [9] и Янбу [10] предложили обобщение следующего вида:

Это уравнение сводится к линейной зависимости жесткости от напряжения при показателе m, равном единице. Таким образом, в частном случае для m = 1 получается логарифмический закон сжатия для нормально уплотненных грунтов.

Для песчаных грунтов показатель степени m значительно меньше и составляет около 0,5 по данным Янбу [10], фон Сооса [11] и других исследователей.

Степенной закон (16) был включен в модель упрочняющегося грунта (модель Hardening Soil, HS), используемую в программном комплексе PLAXIS. Здесь Вермеер [5] отмечает, что Оде [9], Янбу [10] и фон Соос [11] приводили в своих работах следующую формулу:

Вместо вышеуказанного безразмерного коэффициента в модели HS в качестве входного параметра используется Е_oed^ref, то есть одометрический модуль деформации, соответствующий эталонному всестороннему давлению в условиях естественного залегания P_ref = σ^' = 100 кПа.

Разработчики восьмой версии программы PLAXIS (версия PLAXIS V8 должна была выйти вскоре после публикации рассматриваемой заметки Вермеера [5]) обсуждали использование вместо Е_oed^ref альтернативных входных параметров – коэффициента v = 1/λ^*, а также модифицированного коэффициента компрессии λ^*, так как:

Фактически эта простая связь между одометрической жесткостью и модифицированным коэффициентом компрессии и заставила разработчиков задуматься об альтернативных входных параметрах.

Наконец было решено пойти еще дальше и использовать традиционный индекс компрессии C_с, применив в программе следующее уравнение:

В программе PLAXIS теперь есть выбор между вводом E_oed и C_с. Здесь Вермеер [5] отмечает, что при вводе C_с также необходимо задать значение для коэффициента пористости e.

Что касается такого входного параметра, как модуль жесткости при разгрузке и повторном нагружении при компрессионных испытаниях (E_ur), то в качестве альтернативы ему в PLAXIS используется индекс рекомпрессии C_s.

—

Статья подготовлена при поддержке компании «НИП-Информатика» – партнера журнала «ГеоИнфо».

Источники

1. Заметки Питера Вермеера. Как не игнорировать ползучесть грунтов в геотехнической практике? // Geoinfo.ru. 09.12.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/zametki-pitera-vermeera-kak-ne-ignorirovat-polzuchest-gruntov-v-geotekhnicheskoj-praktike-41820.shtml.
2. Заметки Питера Вермеера. Когда нужен «дренированный» и «недренированный» анализ поведения грунтов? // Geoinfo.ru. 18.11.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/zametki-pitera-vermeera-kogda-nuzhen-drenirovannyj-i-nedrenirovannyj-analiz-povedeniya-gruntov-41720.shtml.
3. Заметки Питера Вермеера. О деформационных параметрах моделей грунта и коэффициенте переуплотнения // Geoinfo.ru. 03.02.2020. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/zametki-pitera-vermeera-o-deformacionnyh-parametrah-modelej-grunta-i-koehfficiente-pereuplotneniya-42125.shtml.
4. Заметки Питера Вермеера. Метод конечных элементов (МКЭ) для анализа взаимодействия подпорной стенки и грунта // Geoinfo.ru. 26.03.2020. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/zametki-pitera-vermeera-metod-konechnyh-ehlementov-mkeh-dlya-analiza-vzaimodejstviya-podpornoj-stenki-i-grunta-42395.shtml.
5. Vermeer P. Column Vermeer // Plaxis Bulletin. 2002. № 12. URL: https://www.plaxis.com/content/uploads/2016/10/Plaxis-Bulletin-12.pdf.
6. Terzaghi K., Peck R.B. Soil mechanics in engineering practice. New York: John Wiley and Sons, 1967. 729 p.
7. Wroth C.P., Wood D.M. The correlation of index properties with some basic engineering properties of soils // Canadian Geotechnical Journal. 1987. Vol. 15. № 2. P. 137–145.
8. Engel J. Procedures for the selection of soil parameters: habilitation study. Dresden, Germany: Department of Civil Engineering, Technical University of Dresden, 2001. 188 p. (in German).
9. Ohde J. On the stress distribution in the ground // Bauingenieur. 1939. Vol. 20. № 33/34. P. 451–459 (in German).
10. Janbu N. Soil compressibility as determined by oedometer and triaxial tests // Proceedings of the 3-d European Conference on Soil Mechanics and Foundation Engineering. Wiesbaden, 1963. Vol. 1. P. 19–25.
11. Soos von P. Properties of soil and rock // Grundbautaschenbuch. Berlin: Ernst & Sohn, 2001. Vol. 1. P. 117–201 (in German).

Рис. на заставке:

https://www.plaxis.com/content/uploads/2016/10/Plaxis-Bulletin-12.pdf;

geoengineer.org/education/laboratory-testing/soil-consolidation?utm_source=facebook&utm_medium=social&utm_campaign=page_post.