Статистический подход к расчёту горизонтальных деформаций рек

Введение

В настоящее время оценка горизонтальных смещений речных русел осуществляется преимущественно в соответствии с рекомендациями гидролого-морфологической теории Государственного гидрологического института (ГГИ). Основные положения этой теории изложены в книге [4] и в большинстве отечественных нормативных документов, среди которых можно выделить ВСН 163-83 [1] и СТО ГУ ГГИ [5]. В работе [3] проведён анализ нормативных методов определения горизонтальных деформаций речных русел.

Основным инструментом оценки горизонтальных деформаций выступает метод прямой экстраполяции прошлых значений смещения берегов русла, получаемых путём наложения разновременных картографических материалов (согласно п. 9.4.1–9.4.4 СТО [5]). Метод базируется на наложении друг на друга разновременных картографических материалов (топографические карты и планы, лоцманские карты, космические снимки). В процессе анализа определяются горизонтальное смещение русел (L, м) и временной интервал между датами исходных материалов (T, годы). Прогноз горизонтальных деформаций осуществляется путем экстраполяции полученного значения скорости смещения берега Vфакт = L / T на расчетный период Tрасчет: Lрасчет = Vфакт • Tрасчет.

Недостатком этого подхода выступает отсутствие учета вероятностного характера скорости смещения берега. Прямая экстраполяция не учитывает многовариантность будущих деформаций и природную неравномерность процесса размыва по длине реки и во времени. При этом принятое равенство фактической и прогнозной скоростей смещения берега (Vфакт = Vпрогноз) не отражает природную изменчивость процесса размыва, что может приводить к ошибкам в прогнозировании горизонтальных деформаций.

В настоящей статье представлено развитие изложенного выше метода прямой экстраполяции. Предложение авторов настоящей статьи по улучшению экстраполяции предлагает учёт статистической неравномерности горизонтальных деформаций речных русел. Далее в статье показано обоснование учёта неравномерности размыва на примере участка реки Иртыш, что демонстрирует практическую применимость предлагаемой методики и ее преимущество перед существующими методами прогнозирования. В статье [2] приведена система способов оценки русловых деформаций для разных ситуаций, в том числе упомянут рассматриваемый здесь способ оценки русловых деформаций на основе учета изменчивости размыва.

Профиль предельного размыва

Профиль предельного размыва (ППР) представляет собой расчетный профиль, характеризующий максимально возможные деформации речного русла за заданный период времени. Важно учитывать, что ППР не является фактическим профилем русла на конечный период, а является обобщающей максимальной границей размыва и служит гарантийной линией, обеспечивающей уверенность в том, что фактическое положение русла не выйдет за установленные пределы в течение расчетного периода. При построении ППР основополагающим является принцип презумпции безопасности: все неопределенности, погрешности в расчетах и возможные риски интерпретируются в пользу обеспечения сохранности проектируемого объекта. При этом достижение всех прогнозных точек ППР не является обязательным – профиль демонстрирует лишь максимально возможные положения русла за расчетный период. На основе представлений о ППР как о показателе наибольшего возможного размыва за расчетный период далее приводится статистический способ оценки размыва берега на примере участка реки Иртыш.

Исходные данные и способ обработки плановых материалов

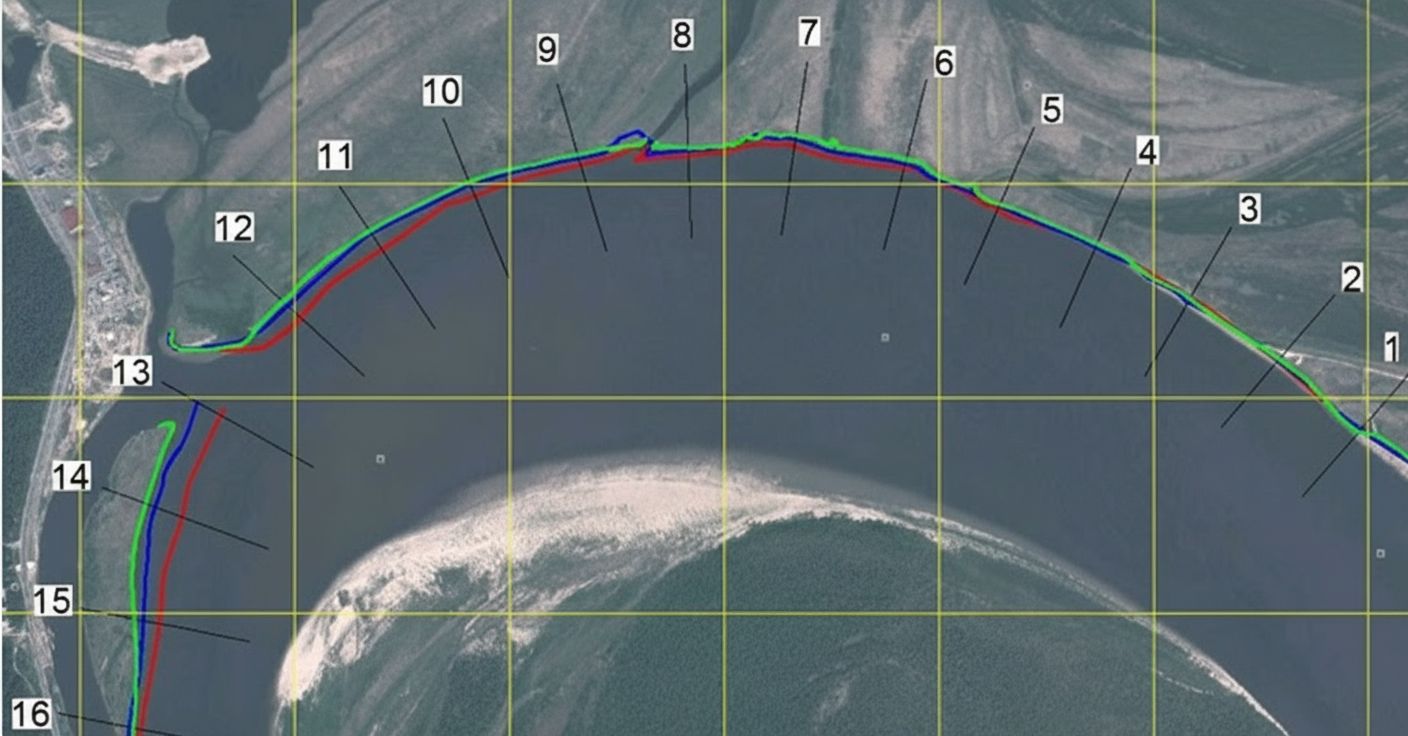
Для демонстрации неравномерности размыва речных берегов был использован участок большой равнинной реки Иртыш в районе устья, расположенный выше города Ханты-Мансийск. Объектом исследования являлся правый берег реки (рис. 1). Этот берег характеризуется как высокий, размываемый, со скоростью отступания от единиц до десятков метров в год. Данный участок был выбран по следующим критериям: относительно высокие скорости горизонтальных размывов, определяемые по космическим снимкам; наличие серии космических снимков за разные годы; возможность выделения однородного участка с квазиоднородными условиями размыва.

Использованы космические снимки Google Earth за 2005, 2009 и 2012 годы. Абсолютная точность таких космических снимков может быть велика. Поэтому выполнено наложение разновременных космических снимков в программе AutoCAD с последующим совмещением по устойчивым контурам (здания, причалы, дороги) с точностью не менее 1 м.

В официальной документации Google, в том числе в справке по Google Earth, прямо не указывается значение точности космоснимков, так как данные поступают из разных источников с разной точностью. Исследования ISPRS указывают среднюю погрешность измерений 4,38 м [6]. Выявленная неравномерность горизонтальных размывов берега включала в себя все погрешности и неточности: как исходных данных, так и точности наложения. При практическом применении разделить вклад этих составляющих невозможно. Поэтому дальнейшая методика по выявлению и оценке неравномерности горизонтальных деформаций русла реки Иртыш не разделяла вклады разных типов погрешностей. Неравномерность может зависеть как от реальных размывов реки, так и от неточности исходных данных, как и происходит в практической работе.

На каждом снимке проведена оцифровка бровок правого берега. Использование бровок берега в качестве основной линии исследования обусловлено следующими преимуществами по сравнению с береговой линией. Во-первых, их положение не зависит от колебаний уровня воды. Во-вторых, они четко выражены как линия перегиба между поймой и обрывистым склоном.

Рис. 1. Совмещенные бровки правого берега исследуемого участка р. Иртыш за 2005 г. (красная линия), 2009 г. (синяя линия) и 2012 г. (зеленая линия).

В результате совмещения материалов получены положения бровки реки Иртыш на исследуемом участке. Участок длиной 4000 м разбит на 16 расчётных створов с интервалом 250 м. Нумерация створов выполнена сверху вниз по течению (с востока на запад). Анализ полученных данных показал наличие двух характерных зон. В восточной (верхней) зоне смещения бровок относительно малы, тогда как в западной (нижней) зоне они заметно больше.

Фактические скорости горизонтальных размывов берега

По намеченным створам измерены фактические расстояния смещения берега и по периодам между датами космических снимков (∆t1 = 2009 – 2005 = 4 года; ∆t2 = 2012 – 2009 = 3 года) вычислены скорости размыва берега. Также рассчитано суммарное смещение бровки за период с 2005 г. по 2012 г. (7 лет) и соответственная средняя за 7 лет скорость размыва. Результаты вычислений приведены в табл. 1.

Таблица 1. Расстояния смещения правого размываемого берега р. Иртыш на участке исследований и скорости размыва

Примечание: положительные значения смещения бровок – размыв, отрицательные значения – намыв.

На рисунке 2 приведено схематическое изображение скоростей размыва берега реки Иртыш на исследуемом участке.

Рис. 2. Скорости размыва берега реки Иртыш на исследуемом участке.

На некоторых поперечниках (№№1, 3, 4, 16) отмечены отрицательные скорости смещения берега, то есть, берег не размывался, а смещался в сторону реки (см. примечание к табл. 1). Чем это вызвано, на данный момент не ясно – фактическим намывом берега, неточностью исходных материалов или неточностью наложения космических снимков. Тем не менее, далее анализ полученных материалов выполнен с полученными значениями, включающими и отрицательные значения.

Как видно из таблицы 1, средняя скорость смещения берега за первый период составила 5,5 м/год, во второй период 3,0 м/год, и в целом за весь срок 4,4 м/год. Чем вызвана такая разность – не ясно. В дальнейшем в настоящей работе использован статистический подход к обработке полученных скоростей размыва берега.

Если формально следовать методу прогноза плановых деформаций, изложенному в действующих документах [1, 5 и др.], то получаются разные прогнозные значения смещения берега за следующие 30 лет: при наличии исходных данных за 2005 г. и 2009 г. и расчетной средней скорости смещения берега 5,5 м/год прогнозное смещение за 30 лет составит 165 м. При наличии исходных данных за 2009 г. и 2012 г. и расчетной средней скорости смещения берега 3,0 м/год за 30 лет прогнозное смещение составит 90 м. При наличии исходных данных за 2005 г. и 2012 г. и расчетный средней скорости смещения берега 4,4 м/год прогнозное смещение составит 132 м.

Как видим, максимальное прогнозное смещение 165 м и минимальное 90 м различаются в 1,8 раза. При этом при отсутствии других данных, каждое из этих значений по имеющимся будет считаться «верным» и использоваться без каких-либо коррекций в дальнейших расчетах. То есть, при одних исходных данных плановое смещение на 30 лет будет дано на 90 м, а при других – на 165 м.

Можно сделать вывод, что статистический анализ длинных рядов требует отдельного изучения. В данной работе в основном рассматривается вопрос о необходимости учета неравномерности размывов берегов и разработки статистического подхода к прогнозу плановых деформаций. Далее в статье предлагается иллюстративный пример возможного статистического расчёта.

Пример статистического расчёта

По длине рассматриваемого участка можно выделить несколько характерных зон. На этих участках наблюдаются как различные скорости плановых размывов, так и разная вариативность этих скоростей. Поэтому на участке длиной 4 км, расположенном в вершине излучины реки Иртыш, выделен относительно короткий участок длиной 750 м – от створа №9 до створа №12. На этом участке были установлены дополнительные поперечники с расстоянием 50 м между ними. Всего было рассмотрено 16 участков.

Рис. 3. Схема расположения детальный створов для статистической характеристики размыва берега реки Иртыш на исследуемом участке. В верхней части общая нумерация створов. В нижней части – нумерация дополнительных створов

По дополнительным створам 1-16 измерены фактические расстояния отступания берега и по периодам между датами космических снимков (∆t1 = 2009 – 2005 = 4 года; ∆t2 = 2012 – 2009 = 3 года) и вычислены скорости размыва берега на участке длиной 750 м от створа №9 до створа №12. Также рассчитано суммарное смещение бровки за период с 2005 г. по 2012 г. (7 лет) и соответственная средняя за 7 лет скорость размыва. Результаты вычислений приведены в таблице 2.

Таблица 2. Измеренные расстояния смещения и скорости размыва правого размываемого берега р. Иртыш на участке детальных исследований от створа №9 до створа №12

Как видно из таблицы 2, средняя скорость смещения берега на рассмотренном квазиоднородном участке длиной 750 м за первый период составила 7,0 м/год, а во второй период 3,5 м/год, и в целом за весь срок 5,5 м/год, то есть, максимальная и минимальная скорость различаются в 2 раза.

Получаются разные прогнозные значения смещения берега за следующие 30 лет: При наличии исходных данных за 2005 г. и 2009 г. 7,0 м/год · 30 лет = 210 м. При наличии исходных данных за 2009 г. и 2012 г. 3,5 м/год · 30 лет = 105 м. При наличии исходных данных за 2005 г. и 2012 г. 5,5 м/год · 30 лет = 165 м.

При отсутствии других данных каждое из этих значений будет считаться «верным» и использоваться без каких-либо коррекций в дальнейших расчетах. То есть, при одних исходных данных плановое смещение на 30 лет будет дано на 105 м, а при других – на 210 м.

Статистические характеристики рядов скоростей плановых деформаций

В таблице 3 приведены статистические параметры рядов размывов берегов по данным детальных поперечников №№1-16 по следующим рядам: 1) I период (2005-2009 г.), 4 года. 2) II период (2009-2012 г.), 3 года. 3) Общий период (2005-2012 г.), 7 лет. 4) Общий ряд за первый и за второй период.

Таблица 3. Статистические параметры рядов скоростей плановых размывов

Моделирование многолетних размывов

По статистическим параметрам, приведенным в таблице 3, выполнено статистическое моделирование 30-летних рядов плановых размывов. Использованы статистические характеристики ряда за общий период (2005-2012 гг.): среднее 5,51 м/год, среднеквадратичное отклонение 1,5 м/год, коэффициент вариации Cv = 0,27. В данном расчете для иллюстрации условно принято нормальное распределение скоростей с указанными средним и среднеквадратичным отклонением. Коэффициент автокорреляции принимался равным нулю (расчёт методом Монте-Карло). Сначала по случайным числам в диапазоне от 0 до 1 получался ряд обеспеченностей, по которым пересчитывались значения нормального распределения с указанным средним и среднеквадратичным отклонением. Подобные расчеты выполнены 10 раз (10 реализаций).

На рисунке 4 приведены модельные ряды скоростей размыва берега при заданных параметрах нормального распределения.

Рис. 4. Модельные ряды скоростей размыва берега.

На рисунке 5 показаны результаты моделирования размывов берега реки Иртыш – семейство интегральных кривых.

Рис. 5. Результаты моделирования размывов берега реки Иртыш (10 реализаций).

В результате получены следующие конечные расстояния, на которые может быть размыт берег реки Иртыш за будущие 30 лет при статистических характеристиках ряда: среднее 167 м; стандартное отклонение 8,3 м; минимум 151 м, максимум 178 м.

При этом, среднее смещение за 30 лет при средней скорости размыва 5,5 м/год, полученной по фактическим данным, составило бы 5,5 м/год · 30 лет = 165 м.

Как видно, результирующее смещение берега за расчетный период 30 лет может находиться, как минимум, в диапазоне от 151 м до 178 м. Соответственно, средняя скорость при 10 модельных реализациях размыва составляет от 5,0 м/год до 5,9 м/год.

Отсюда можно сделать вывод, что фактическая реализация размыва берега за 30 лет даже при явно заниженных параметрах среднеквадратичного отклонения ряда скоростей размыва берега может изменяться в пределах ±10% и более от считающегося верным среднего значения.

Для практических расчётов обычно интересует не средняя скорость размыва, а максимальная. Следовательно, полученное «верное» среднее значение скорости смещения берега необходимо увеличивать, в данном примере – на 10%, а в реальных ситуациях при изыскании и проектировании для учёта возможных погрешностей и обеспечения запаса надёжности, как минимум на 20%. Этот подход позволяет учесть возможный вариант, что в прошлом могла быть реализована минимальная скорость, а на будущее для практического использования нужно использовать максимальные значения.

Выводы

1. Существующая методика прямой экстраполяции на будущее прошлых горизонтальных деформаций речных русел, основанная на нормативных документах ГГИ, имеет существенный недостаток – игнорирование вероятностного характера фактических значений скорости смещения и многовариантности будущих деформаций.

2. Предложенный в работе статистический подход к оценке горизонтальных деформаций речных русел позволяет учитывать как неравномерность процесса размыва по длине реки и во времени, так и точность использованных плановых материалов, что существенно повышает надёжность обоснования профиля предельного размыва, основанного на презумпции безопасности: все неопределенности, погрешности в расчетах и возможные риски интерпретируются в пользу обеспечения сохранности проектируемого объекта.

3. На основе анализа фактических данных по участку реки Иртыш установлено, что скорости размыва берега могут существенно различаться как по длине реки, так и во времени. На рассматриваемом участке разница между максимальной и минимальной скоростью размыва составила до 2 раз.

4. Статистическое моделирование 30-летних рядов плановых размывов показало, что фактическая реализация размыва берега может изменяться в пределах ±10% от среднего значения даже при явно заниженных параметрах среднеквадратичного отклонения. Рекомендуется при прогнозе плановых деформаций в полученные значения фактических скоростей плановых деформаций вводить повышающий коэффициент k>1, учитывающий неточность фактических скоростей плановых деформаций рек. При этом прогноз плановых деформаций выполняется в следующей последовательности: Определение фактической скорости: определение фактического прошлого смещения берега L, м, и соответствующего времени t, годы; расчёт прошлой скорости смещения V = L/t, м/год; переход от фактической к максимальной скорости. Vmax = k•V; определение расчётного смещения (Lрасчёт, м) на расчётный период (Tрасчёт, годы) Lрасчёт = Tрасчёт•Vmax. Рекомендуется увеличивать полученную среднюю скорость смещения берега как минимум на 20% в целях обеспечения безопасности при практических расчетах.

5. Полученные результаты подтверждают необходимость перехода при прогнозировании горизонтальных деформаций речных русел от детерминированных методов расчёта к вероятностно-статистическим. В инженерных изысканиях практикующие гидрологи ощущают необходимость учета неравномерности размыва и на основе опыта увеличивают скорости размыва на будущий период. Необходимо узаконить такие действия и разработать новый нормативный документ, в котором учитываются неравномерности размывов берегов и статистические характеристики плановых размывов.

Список литературы

1. ВСН 163-83. Учёт деформаций речных русел и берегов водоёмов в зоне подводных переходов магистральных трубопроводов (нефтегазопроводов). Миннефтегазстрой. Л., Гидрометеоиздат, 1985, 144 с.
2. Кондратьев А.Н., Поваляев Н.Р. Обзор способов обоснования профиля предельного размыва речных русел // Гидротехника. 2024. №1. С. 15-21.
3. Кондратьев А.Н., Поваляев Н.Р., Гордеева Н.И., Стрюцкая А.О. Анализ современного состояния нормативной базы по оценке плановых (горизонтальных) русловых деформаций водотоков // Гидротехника. 2024. № 2. С. 34-38.
4. Кондратьев Н.Е., Попов И.В., Снищенко Б.Ф. Основы гидроморфологической теории руслового процесса. Л.: Гидрометеоиздат, 1982. 272 с.
5. СТО ГУ ГГИ 08.29-2009. Учет руслового процесса на участках подводных переходов трубопроводов через реки. Государственный гидрологический институт. СПб., Нестор-История, 2009, 184 с.
6. Wang, X. W., Wang, F. The Precision of Google Earth Map Analysis with the Coordinates of IGS Stations // ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. 2020. Vol. XLII-3/W10. P. 1053-1056.