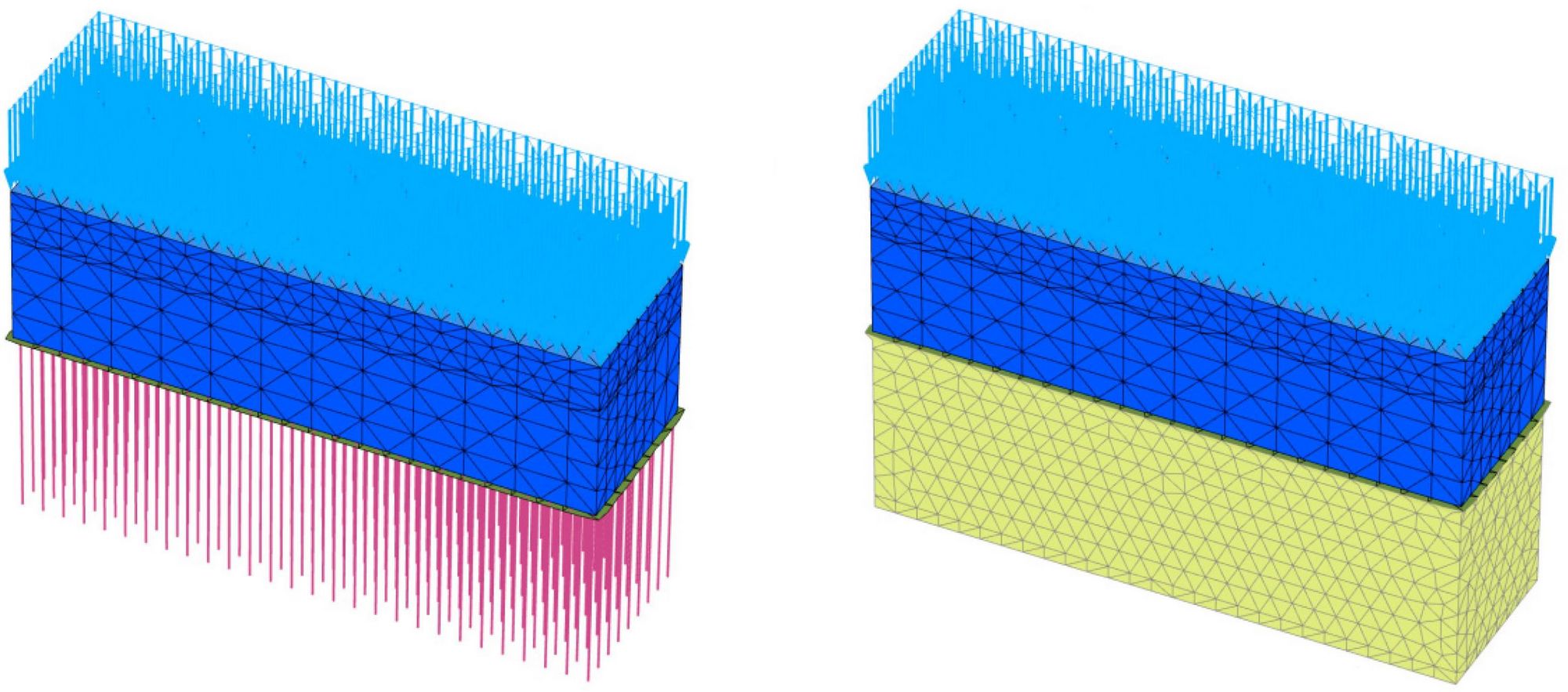
Трехмерный численный анализ взаимодействия подземной части многоэтажного здания и ее грунтового основания, усиленного сваями CFG

Яо Янпин (Yao Yangping)

Институт теории и проектирования транспорта Бэйханского университета (Пекинского университета авиации и космонавтики), г. Пекин, Китай

Сунь Яньфан (Sun Yanfang)

Институт архитектуры и гражданского строительства Тайюаньского технологического университета, г. Тайюань, провинция Шаньси, Китай, sunyanfang@tyut.edu.cn

Хэ Юйхао (He Yuhao)

Факультет гражданского строительства Шаньсийского университета, г. Тайюань, провинция Шаньси, Китай), heyuhao.sx@gmail.com

Чжан Хайцин (Zhang Haiqing)

Колледж гражданского строительства и архитектуры Хэбэйского Университета, г. Баодин, провинция Хэбэй, Китай, haiqzhang@163.com

1. ВВЕДЕНИЕ

Свайно-плитные фундаменты широко используются в Европе и Азии с тех пор, как Дэвис и Поулос [1] предложили в 1972 году аналитический метод для решения связанных с ними задач. Однако в обычном свайно-плитном фундаменте связь между сваями и фундаментной плитой имеет строгие ограничения. В частности, когда количество свай небольшое, а расстояние между ними велико, в плите легко могут возникать большие изгибающие моменты, даже приводящие к ее растрескиванию и концентрации напряжений на верхних концах свай [2]. Чтобы решить эту проблему, между плитой и верхом свай может быть устроен амортизирующий слой (так называемая подушка) определенной толщины [3]. Это помогает использовать несущую способность грунта между сваями для регулирования механизма передачи нагрузок [4–7].

Многие исследователи изучали работу свайно-плитных фундаментов в песке при соединении верхних концов свай с плитой напрямую или через подушку с помощью испытаний моделей на центрифугах [8–13]. Так, в статьях [8] и [9] представлены результаты обширных испытаний на вертикальные и эксцентрические статические нагрузки. Авторы публикаций [10–12] изучили работу указанных двух типов фундаментов с помощью серии испытаний моделей на центрифугах. Для случая соединения плиты со сваями через подушку в статье [13] предложен упрощенный вид разрушения, включая подушку, и соответствующий теоретический анализ. А авторы работ [14] и [15] подчеркнули важность грунтовой подушки в регулировании передачи нагрузок от свай грунту на основе полевых испытаний на статические нагрузки.

При наличии амортизирующего слоя происходит множество взаимодействий между плитой, подушкой, сваями и грунтом. Для такой сложной системы эффективным инструментом расчета является метод конечных элементов (МКЭ). Авторы статей [16–22] изучали механизмы передачи нагрузок и характеристики осадок свайно-плитных фундаментов с амортизирующими подушками с помощью трехмерного анализа на основе МКЭ. В этих исследованиях было принято, что сваи находятся в однородном грунте, а для моделирования свай использовались объемные (3D) элементы. С увеличением количества свай растет сложность и многокомпонентность сеток конечных элементов, что в конечном итоге приводит к увеличению времени, необходимого для численных расчетов [19]. Чтобы преодолеть эти недостатки, Садек и Шахрур [23] предложили новый способ моделирования свай в виде одномерных стержневых элементов (далее погруженных свай – embedded piles), а Чучниг и Швайгер [24] усовершенствовали его. В этом методе погруженный свайный элемент не учитывался при создании сетки грунта, что уменьшило количество степеней свободы расчетной модели и повысило эффективность расчета. Традиго с соавторами [25] впервые изучили применимость и точность метода моделирования погруженной (1D) сваи при наличии подушки между ее верхом и фундаментной плитой и отметили, что осадки при использовании этого метода обычно близки к таковым при использовании метода объемной (3D) сваи.

Лян с соавторами [7] предложили упрощенную аналитическую модель для оптимального выбора жесткости подушки. Чжао с коллегами [26] разработали методику расчета осадок свайно-плитного фундамента с длинными и короткими сваями. Чжан и Ши [27] построили механическую модель пронизанной сваями подушки и метод расчета взаимодействия сваи с грунтом. Они использовали их, чтобы предложить метод теоретического расчета коэффициента напряжения в системе «свая – грунт».

Большинство вышеперечисленных исследований было сосредоточено на несущей способности и деформационном поведении свайно-плитных фундаментов для отдельных зданий в идеальных и упрощенных условиях. В основном проводился анализ геометрических параметров сваи, плиты и подушки, а площадь плиты и количество используемых свай сильно отличались от используемых на практике. Мало внимания было уделено ситуациям, связанным с подземными этажами и уж тем более случаям, когда на одной и той же плите были построены и много-, и малоэтажные здания.

Поэтому в настоящей статье обсуждается методика численного моделирования свайно-плитных фундаментов с упором на проблему контроля осадок много- и малоэтажных зданий с подземными этажами. Также предлагается упрощенный метод эквивалентного 3D численного моделирования основания фундаментной плиты, армированного буронабивными сваями из перспективного строительного материала CFG (Cement – Fly ash – Gravel, или «цемент – зольная пыль – гравий»), то есть грунтоцементными сваями с добавлением зольной пыли, чтобы преодолеть трудности плохой сходимости результатов вычислений, вызванной слишком большим количеством свай. В этом методе усиленная зона, рассматривается как единое тело из анизотропного материала, параметры жесткости которого получаются путем обратного расчета в соответствии с заданными значениями осадки и горизонтальной деформации. В случае применения этого метода к практическим случаям можно обнаружить, что результаты расчетов удовлетворяют требованиям точности проектирования, диапазон применения соответствующего численного моделирования становится шире, а эффективность численных расчетов повышается. Все это дает проектировщикам основу для оптимизации проектных решений и вычисления осадок фундаментов, а также для эффективного поиска практических идей по применению численного моделирования для совместных расчетов деформаций различных частей фундаментов.

2. АНАЛИЗ ОСАДОК КОМБИНИРОВАННОГО ФУНДАМЕНТА СО СВАЯМИ CFG

2.1. Теоретический анализ

Деформирование композитного основания, состоящего из грунта и армирующих грунтоцементных свай CFG, можно разделить на две части: деформацию в усиленной зоне S₁ и деформацию в нижележащем слое S₂. Для усиленной зоны сваи CFG и естественный грунт рассматриваются как единое целое, а для расчета деформации композитного основания используется подходящий для него компрессионный модуль деформации. Для расчета деформации нижележащего слоя используется компрессионный модуль деформации естественного основания. На основе работы [28] окончательная деформация S композитного основания со сваями CFG может быть рассчитана по следующей формуле:

Расчет напряжений основан на теории изотропной однородной линейной деформации. Нелинейные характеристики грунта, влияние траектории напряжения на его деформирование, деформация разгрузки и повторного нагружения (rebound-recompression deformation) в этой теории не рассматриваются (как и в общепринятой в России теории расчета осадок. – Ред.). В ней не учитывается также влияние трехмерного пространства, из-за чего не отражается воздействие больших нагрузок в прилегающей зоне на напряженно-деформированное состояние грунта. Более того, в этих теоретических расчетах не может быть учтено и взаимодействие между фундаментной конструкцией под действием нагрузки сверху и грунтом.

2.2. Численный анализ

2.2.1. Объемные элементы и интерфейсы

При анализе работы свайно-плитного фундамента методом конечных элементов для моделирования сваи обычно используется объемный (трехмерный) элемент, и, таким образом, взаимодействие сваи с грунтом учитывается путем введения интерфейсных элементов [16–18, 22]. Обычно это модель интерфейса нулевой толщины, предложенная Гудманом с соавторами [29]. Узлы по обе стороны от интерфейса находятся в одной и той же системе координат, которая может использоваться для моделирования взаимного поведения грунта и конструкции, такого как относительное проскальзывание и разделение. Этот метод интуитивно понятен для моделирования. Смещение и напряжение тела сваи могут быть интуитивно получены при последующей обработке результатов. Однако во время конечноэлементого расчета свая и грунт соединены вместе (единой сеткой), при этом значения их жесткости явно различаются и взаимодействие между ними является относительно сильным. Поэтому необходимо локально уточнить конечноэлементную сетку в определенном диапазоне тела сваи и вокруг нее, чтобы обеспечить качество всей сетки и сходимость расчетов. Это значительно увеличивает общее количество элементов сетки и их типов и увеличивает длительность вычислений. А когда количество свай велико, проблема еще больше усложняется. Кроме того, внутреннее усилие в свае не может быть напрямую определено при использовании объемного свайного элемента.

В целом, моделирование объемных свайных элементов подходит в случаях, когда требуется меньше свай. При большом же их количестве возникает ряд проблем, таких как увеличение числа элементов сетки и их типов, увеличение времени расчетов и плохая сходимость результатов вычислений.

2.2.2. Погруженный свайный элемент

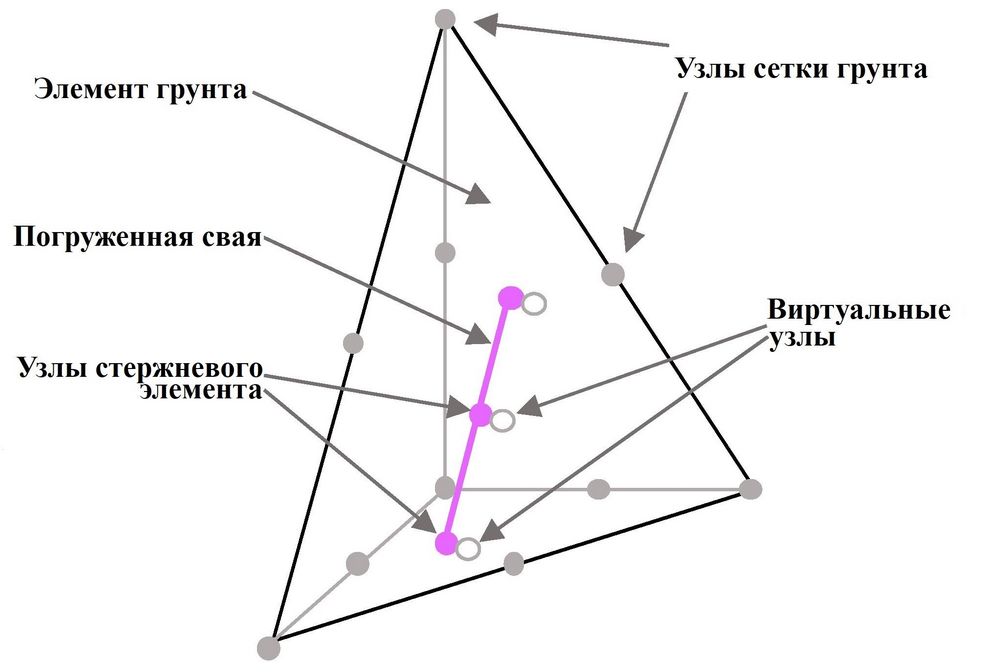
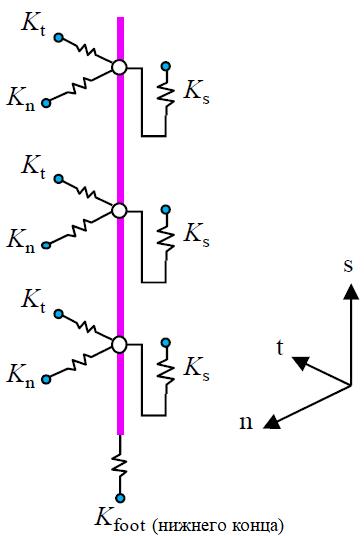
Погруженный (embedded) свайный элемент – это одномерный (1D) стержневой элемент, который не участвует в сетке трехмерных элементов грунта и может быть установлен в любом положении и в любом направлении в объемной сетке грунта. Вдоль сваи могут быть созданы виртуальные узлы (рис. 1). Погруженная свая взаимодействует с окружающим грунтом через собственные интерфейсные элементы. Несущая способность конца сваи моделируется с помощью нижнего пружинного (упругого) элемента (bottom spring element). Трение по боковой поверхности сваи и усилие в ее нижнем конце (сопротивление грунта под нижним концом) определяются через относительное смещение сваи и грунта (рис. 2). Поскольку погруженный свайный элемент не влияет на создание сетки грунта (по сравнению с моделированием объемной сваи), то может быть в значительной степени уменьшено общее количество элементов модели и повышена эффективность расчетов. Также могут быть быстро созданы смещения и внутренние усилия в свае. Авторы работ [24, 25, 30] верифицировали работу одной сваи, свайного куста и свайно-плитных фундаментов, смоделированных с использованием погруженного (1D) свайного элемента вместо объемного (3D).

Рис. 1. Погруженная свая в 10-узловом тетраэдрическом (объемном) грунтовом элементе

Рис. 2. Жесткость погруженных интерфейсных элементов на боковой поверхности и под нижним концом сваи

2.2.3. Метод эквивалентной замены

Когда размеры фундаментной конструкции или количество свай особенно велики (например, сотни или даже тысячи свай) или здание/сооружение имеет сложную форму (например, имеет подземные этажи и/или состоит из нескольких или множества надземных частей), то результаты расчетов бывают некорректными из-за большого числа элементов, что легко может привести к появлению сильно деформированных элементов и сложных взаимодействий, вызванных большим количеством контактных поверхностей между грунтом и конструкциями. Методы с использованием объемных (3D) свайных элементов и интерфейсов и даже погруженных (1D) свайных элементов в данном случае не могут соответствовать требованиям оперативной оценки надежности проекта на практике.

В настоящей статье предлагается упрощенный метод, основанный на эквивалентном моделировании в случае большого количества свай CFG, когда сваи для вертикального армирования и грунт рассматриваются как анизотропное целое. Тогда сваи, моделируемые с использованием погруженных (1D) или объемных (3D) свайных элементов, в модели не нужны. Вместо этого параметры жесткости и прочности всей армированной зоны заменяются эквивалентными значениями осадок и их распределением.

Свая CFG представляет собой своего рода геополимер с большой силой сцепления, полученный из смеси цемента, зольной пыли, заполнителя (например, гравия) и воды. Его материальный состав и механические свойства аналогичны обычному бетону. Прочность материала сваи CFG обычно определяется посредством испытания на предел прочности при одноосном сжатии [31, 32].

При численных расчетах в конечноэлементном программном комплексе PLAXIS эквивалентная армированная зона рассматривалась как единое тело из анизотропного упругопластического материала, для которого использовалась комплексная геомеханическая модель скального грунта (Jointed Rock). Основными параметрами этой модели были плотность ρ, удельное сцепление c, угол внутреннего трения ϕ, модули упругости E₁ и E₂ и коэффициенты Пуассона ν₁ и ν₂ в горизонтальном и вертикальном направлениях соответственно, а также модуль сдвига G₂ в вертикальном направлении.

Плотность выражалась как средневзвешенное значение плотности каждого слоя грунта в зависимости от его толщины в усиленной зоне. Удельное сцепление получили с использованием прочности цемента сваи CFG. Угол внутреннего трения ϕ был принят нулевым. Коэффициенты Пуассона ν₁ и ν₂ составляли 0,3. Модули упругости E₁ и E₂ были получены путем обратного расчета в соответствии с заданными осадкой и горизонтальной деформацией, а модуль сдвига G₂ был определен в зависимости от E₂ и ν₂.

Метод эквивалентного интегрированного моделирования практичен для трехмерного численного анализа взаимодействия между фундаментной плитой многоэтажного здания и ее композитным основанием с большим количеством свай CFG в грунте. Возможности и практическое применение этого метода представлены в следующих разделах.

3. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ПОВЕДЕНИЯ СИСТЕМ «СВАЯ – ПЛИТА»

3.1. Численное моделирование

3.1.1. Краткое описание конкретного случая проектирования

Были взяты данные инженерных изысканий на площадке строительства в Пекине (Китай). Порядок расположения слоев грунта сверху вниз там был следующим:

1) глинисто-илистый грунт (clay silt);

2) песчано-илистый грунт (sandy silt);

3) пылеватый песок (silty-fine sand);

4) пылеватая глина (silty clay);

5) песок от мелкозернистого до среднезернистого (fine-medium sand);

6) пылеватая глина (silty clay).

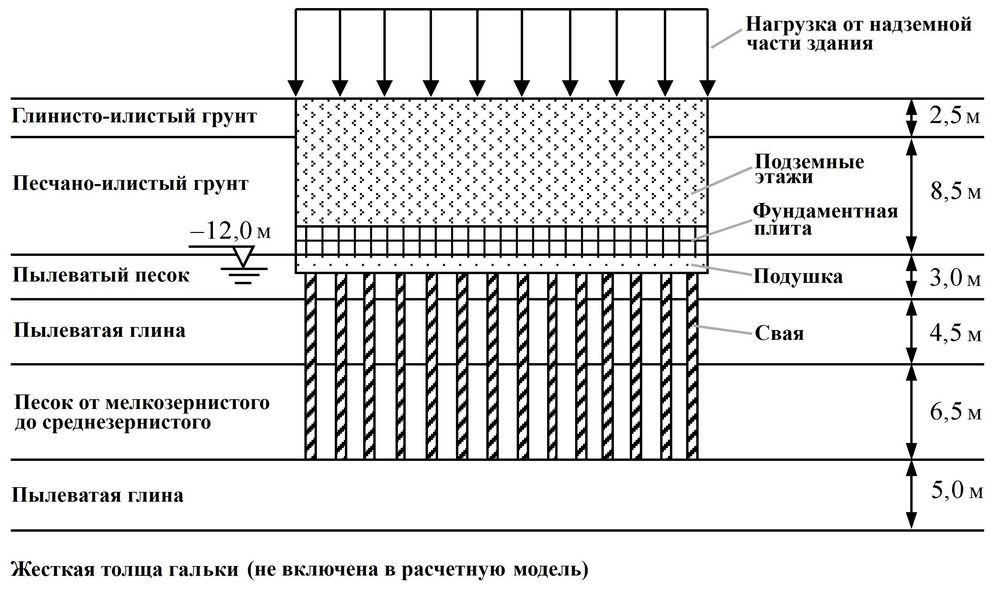
Толщина перечисленных слоев составляла 2,5; 8,5; 3,0; 4,5; 6,5 и 5,0 м соответственно (рис. 3). Под ними залегала галька. Глубина залегания грунтовых вод была 12 м.

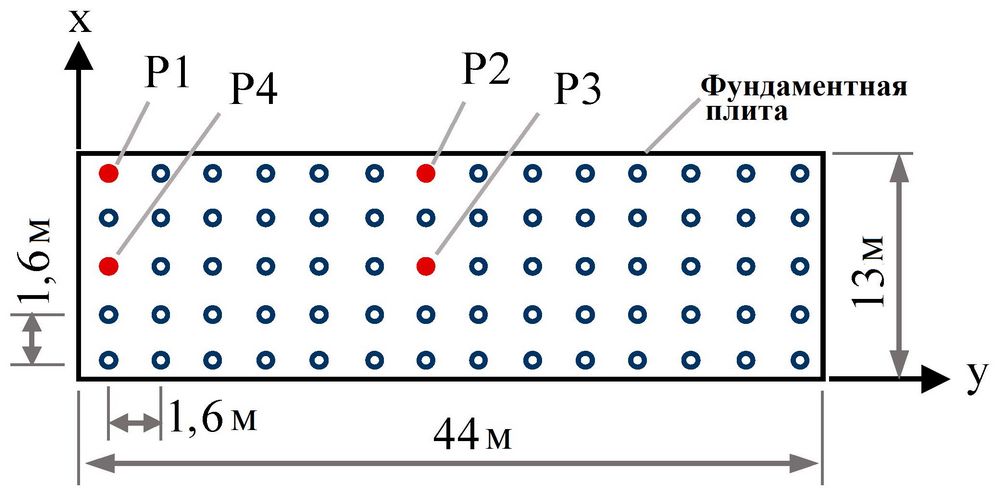
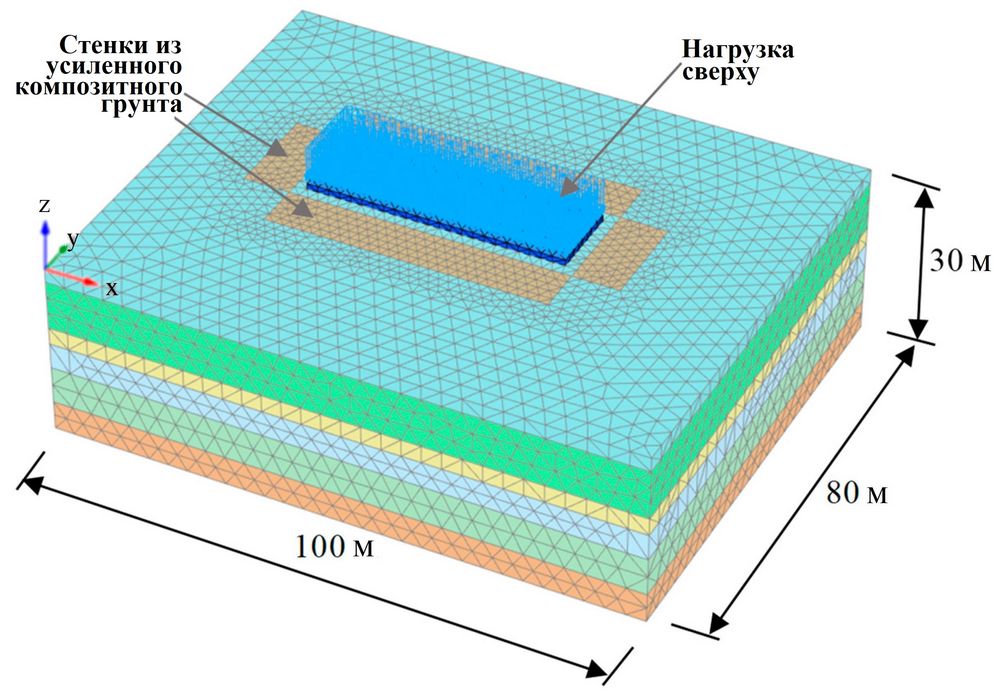
На этой площадке должно было быть построено многоэтажное здание с 3 подземными этажами и 17 надземными этажами. Глубина выемки грунта под котлован для подземных этажей составляла 11 м. Борта котлована был укреплены стенкой из усиленного композитного грунта (nailing wall of composite soil). Естественное грунтовое основание не соответствовало требованиям к несущей способности и осадкам здания и было стабилизировано с использованием буронабивных свай CFG диаметром 400 мм при расстоянии между соседними сваями 1600 мм и использовании цементного бетона класса C25 (cement concrete C25) (рис. 4). Толщина подушки между подошвой подземной части здания и сваями составляла 200 мм. Нагрузка от каждого этажа составляла приблизительно 15 кПа. Она была преобразована и приложена к кровле подземной части.

Рис. 3. Схематический вертикальный разрез расчетной модели

Рис. 4. Схематический горизонтальный разрез расчетной модели

3.1.2. Построение модели

С помощью программного комплекса PLAXIS 3D была создана трехмерная численная модель вышеуказанного здания.

Размер модели. В соответствии с размером свайно-плитного фундамента и глубиной выемки грунта при строительстве котлована под подземную часть здания длина и ширина модели были определены в два раза больше глубины выемки путем нескольких изменений размеров и перестраиваний модели. По высоте модель заключалась между поверхностью земли и кровлей твердой толщи гальки. Ее окончательные длина, ширина и высота составили 100; 80 и 30 м соответственно.

Выбор конечных элементов. Грунт и подушка были разбиты на десятиузловые тетраэдрические элементы. Для моделирования пола, стен подземной части здания и фундаментной плиты использовались шестиузловые плитные элементы. Для моделирования опор подземной части здания – трехузловые балочные элементы. Для моделирования свай CFG – погруженные свайные элементы. Между подушкой и подошвой подземной части здания был добавлен интерфейс, чтобы смоделировать взаимодействие между подошвой железобетонной фундаментной плиты и несвязным грунтом подушки с учетом разницы в жесткости между ними. Использованные интерфейсные элементы были нулевой толщины [29].

Параметры интерфейса в PLAXIS связаны с параметрами окружающего грунта (то есть материала подушки в данном случае) через коэффициент R_inter. В этом исследовании коэффициент R_inter был установлен равным единице. Когда была сгенерирована сетка модели (глобальная крупность элементов установлена как «очень мелкая» – very fine), сетка вокруг свайно-плитного фундамента была локально измельчена. Общее количество объемных элементов составило более 100 000. Сетка модели показана на рисунке 5.

Рис. 5. Трехмерная модель,  разбитая сеткой конечных элементов

Материальные параметры и модель. В данном исследовании грунт и подушка считались упругопластическими. Использовалась такая комплексная геомеханическая модель, как модель упрочняющегося грунта (Hardening Soil – HS), которая подходит для анализа его механического поведения при нагружении и разгрузке. Входные параметры модели HS включали:

• секущий модуль деформации (жесткости) при испытании грунта на трехосное сжатие в дренированных условиях E₅₀^ref;
• касательный модуль деформации (жесткости) при первичном одометрическом нагружении E_oed^ref;
• жесткость при разгрузке и повторном нагружении E_ur^ref;
• показатель степени m в формуле, выражающей зависимость жесткости от уровня напряжений;
• коэффициент Пуассона ν;
• удельное сцепление c;
• угол внутреннего трения ϕ.

Эти параметры были определены с помощью метода, предусмотренного в PLAXIS. Величины E_oed^ref и ν были оценены эмпирически, в то время как в PLAXIS по умолчанию установлено, что E₅₀^ref = E_oed^ref, E_ur^ref = E₅₀^ref и m = 0,5. Другие параметры были получены с помощью основных геотехнических, трехосных и компрессионных испытаний (consolidation tests) [33].

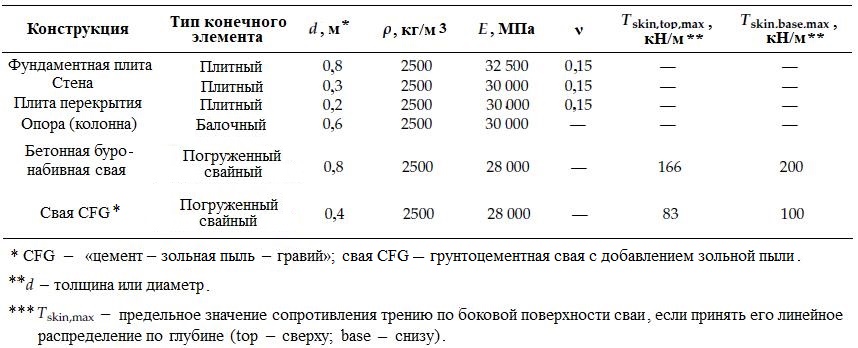
Для подушки использовалась идеально-упругопластическая модель в соответствии с критерием Мора – Кулона. Было принято, что подземные этажи, стены, опоры, плиты и сваи находятся в линейно-упругом состоянии. Более того, поскольку данная статья посвящена в основном анализу осадок здания, окружающая котлован зона стенки из усиленного композитного грунта при создании котлована для подземной части здания была задана как эквивалентный объем грунта с повышенными значениями параметров прочности и жесткости. Параметры грунта были определены на основе отчетов по инженерным изысканиям, геотехнических испытаний и инженерного опыта, а параметры конструкционных материалов были преобразованы в соответствии с разрезами конструкций и типами материалов, как показано в таблицах 1 и 2.

Таблица 1. Физико-механические параметры грунта

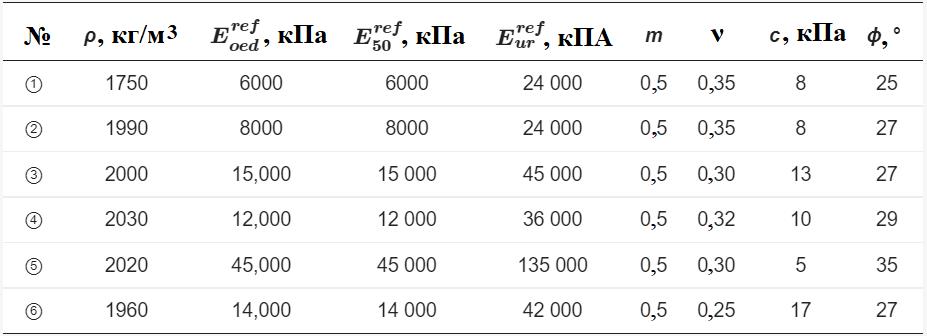
Таблица 2. Материальные параметры конструкций

Граничные условия. Граничные условия модели были назначены как обычные статические. Верхняя поверхность модели была свободной по всем направлениям. Ее боковая граница поддерживалась скользящей заделкой (sliding hinges), которая ограничивала горизонтальное, но не вертикальное перемещение. Нижняя граница модели была фиксированной по всем направлениям.

3.1.3. Материальные параметры эквивалентной армированной зоны

Эквивалентная армированная зона основания фундаментной плиты со сваями CFG рассматривалась как единое тело из анизотропного упругопластического материала, и его механическое поведение описывалось с помощью модели скального грунта (Jointed Rock model). Параметры модели включали жесткость E₁ и коэффициент Пуассона ν₁ в горизонтальном направлении (α₁ = 0 град.) и соответствующие параметры E₂ и ν₂ в вертикальном направлении (α₂ = 90 град.). Прочностные параметры сваи CFG были приняты следующими: c = 270 кПа; ϕ = 0 град.

Ключевым моментом является определение двух наборов параметров жесткости во время численного моделирования с использованием модели скального грунта. В этом исследовании было принято, что ν₁ = ν₂ = 0,35, и на этой основе E₁ и E₂ были определены пробными расчетами. Этот процесс заключался в следующем.

1. Для обеспечения точности расчета для сваи и подушки была создана тестовая однорядная модель свай, а сетки слоя грунтовой подушки и основания в определенном диапазоне длины сваи были локально уточнены для получения 5–10 элементов вокруг каждой сваи (сетка этой модели показана на рисунке 6);

2. Параметры модели для эквивалентного композитного основания фундаментной плиты (E₁ и E₂) были получены путем «подгонки» к вертикальной деформации (то есть к оседанию) и к горизонтальной деформации вне сваи.

В случае принятия ν₁ = ν₂ = 0,3 первым шагом было сделать равными E₁ и E₂, чтобы это соответствовало вертикальной деформации, а затем подобрать E₁ так, чтобы это соответствовало горизонтальной деформации. Затем удовлетворительные результаты калибровки были получены путем небольшой корректировки E₂. После трех циклов вышеуказанного пробного расчета было установлено, что E₁ = 1,0 x 10⁴ кПа, E₂ = 1,2 x 10⁵ кПа и G₂ = 0,5E₂/(1 + ν₂) = 4,62 x 10⁴ кПа.

Рис. 6. Сетка однорядной модели свай: а – схема интегральной модели в вертикальном разрезе; б – увеличенная деталь в 3D

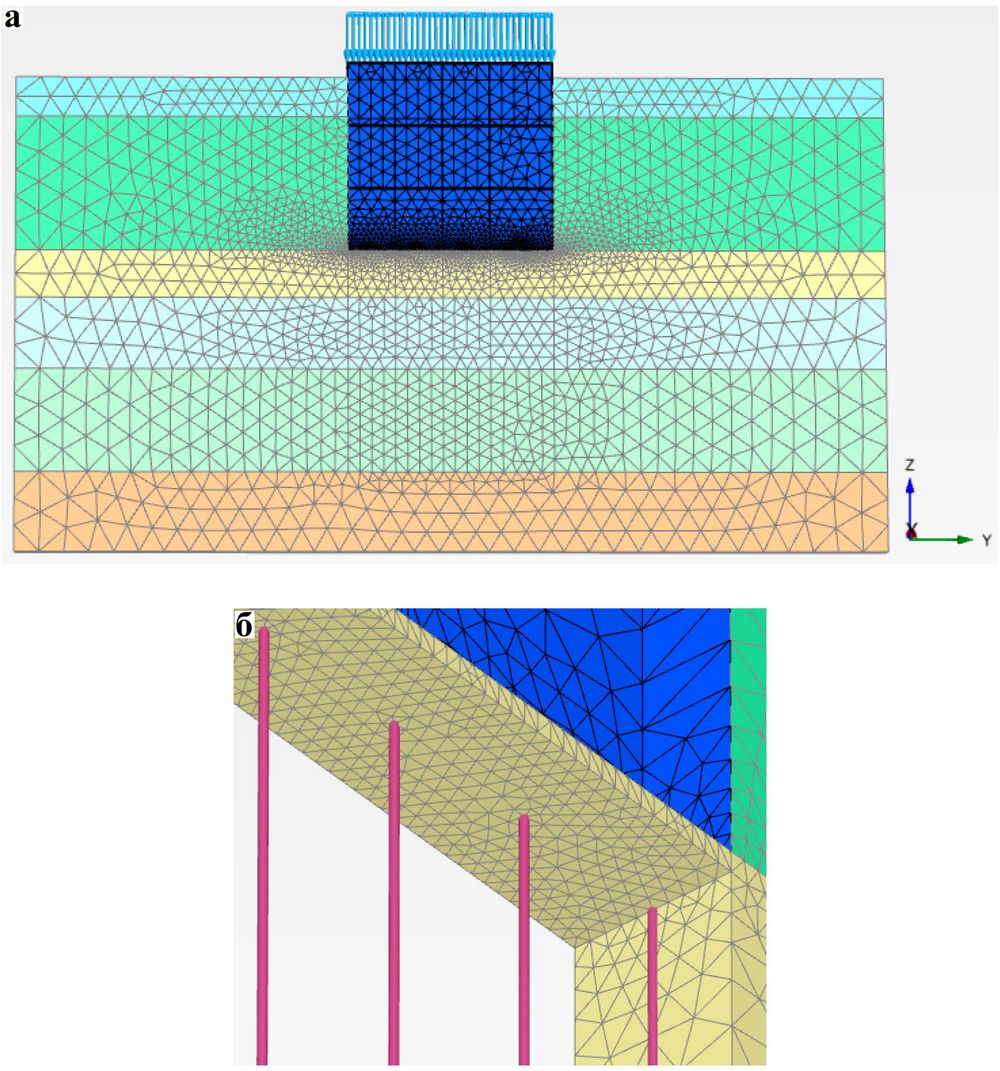
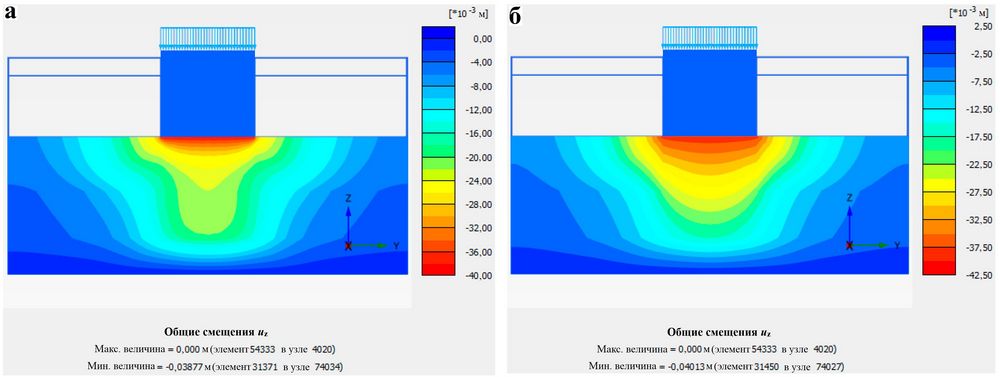
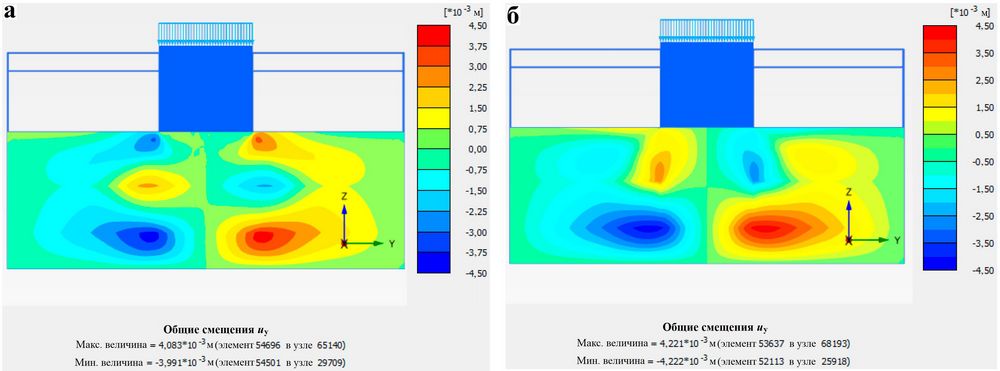
На рисунках 7 и 8 сопоставлены соответственно вертикальные и горизонтальные деформации для модели с использованием погруженных свай и для описанной выше эквивалентной модели. Было показано, что численные результаты, полученные с применением этих двух моделей, очень близки между собой и что эквивалентные параметры являются вполне подходящими.

Рис. 7. Сравнение вертикальных деформаций подушки между подошвой фундаментной плиты и сваями: а – для модели с использованием погруженных свай; б – для модели эквивалентной армированной зоны

Рис. 8. Сравнение горизонтальных деформаций подушки между подошвой фундаментной плиты и сваями: а – для модели с использованием погруженных свай; б – для модели эквивалентной армированной зоны

3.2. Схемы численных расчетов

С целью проверки возможности использования свай CFG для армирования грунтовых оснований многоэтажных зданий были использованы четыре схемы численных расчетов свайно-плитных фундаментов.

Схема 1. Фундаментная плита + бетонные буронабивные сваи (свая моделируется погруженным свайным элементом). Верх сваи жестко соединяется с плитой. Длина сваи составляет 14 м, диаметр – 0,8 м; расстояние между соседними сваями – 3,2 м (рис. 9, а).

Схема 2. Фундаментная плита + подушка + бетонные буронабивные сваи (свая моделируется погруженным свайным элементом). Толщина подушки составляет 200 мм, а параметры свай – такие же, как в первом случае (рис. 9, б).

Схема 3. Фундаментная плита + подушка + сваи CFG (свая моделируется погруженным свайным элементом). Длина сваи составляет 14 м, диаметр – 0,4 м, расстояние между соседними сваями – 1,6 м (рис. 9, в). Кроме того, на основе схемы 3 и эквивалентного интегрального метода, предложенного в разделе 2.2.3, была разработана схема 4.

Схема 4. Фундаментная плита + эквивалентная усиленная зона, причем подушка включена в эту зону (рис. 9, г).

Рис. 9. Модели свайно-плитного фундамента для схем моделирования 1 (а), 2 (б), 3 (в) и 4 (г). Схемы моделирования 1–4 описаны в тексте ранее.

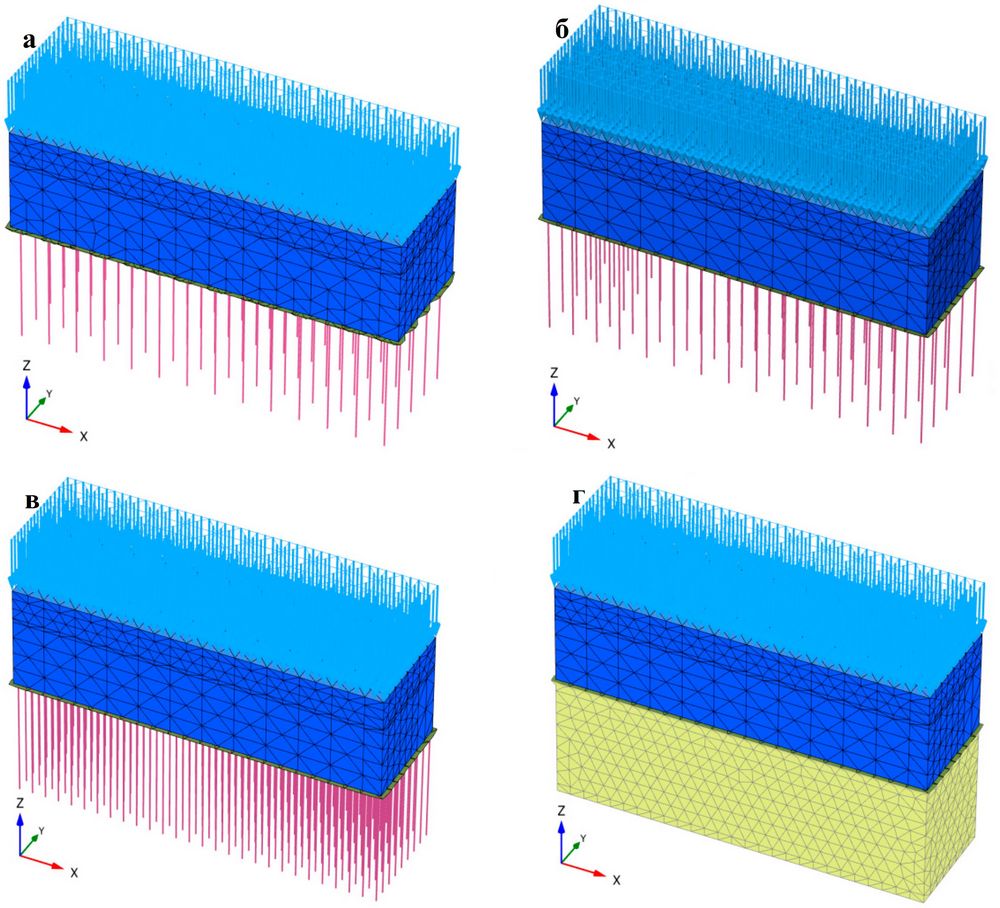
Смоделированная процедура расчетов для четырех вышеуказанных схем заключалась в следующем:

1) расчет природного напряженного состояния;

2) выемка грунта под котлован для подземной части здания, активация зоны стенки из усиленного грунта;

3) устройство свай ниже дна котлована, активация погруженных свайных элементов (для схем 1, 2 и 3) или уточнение эквивалентных параметров армированной зоны (для схемы 4);

4) активация фундаментной плиты и ее основания, приложение нагрузки, активация соответствующих структурных элементов, интерфейсных элементов, поверхностной нагрузки;

5) обратная засыпка вокруг подземной части здания и расчеты до сходимости результатов.

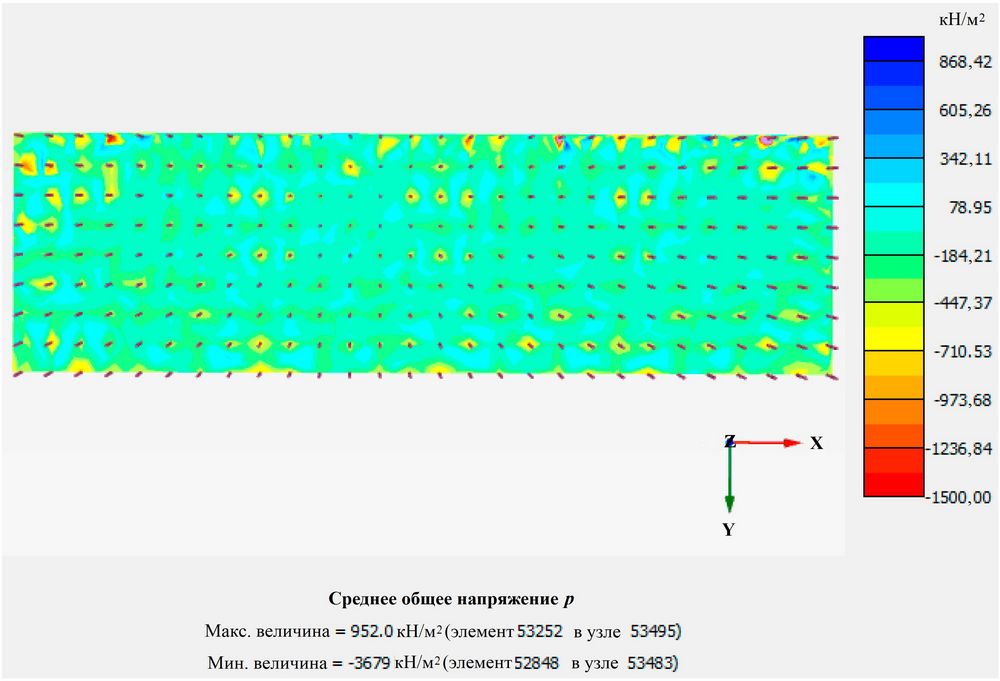
Чтобы повысить точность расчетов на основе схемы 2, было проведено специальное моделирование для грунтовой подушки путем уточнения сетки конечных элементов этого слоя таким образом, чтобы можно было должным образом отразить концентрацию напряжений на верхнем конце сваи. Можно увидеть, что общее среднее напряжение p грунтовой подушки было распределено равномерно (рис. 10), что позволило эффективно избежать чрезмерной концентрации локальных напряжений на верхнем конце сваи, обеспечив точность расчетов.

Рис. 10. Распределение главных напряжений в подушке

3.3. Полученные результаты и их обсуждение

3.3.1. Поведение фундаментной плиты

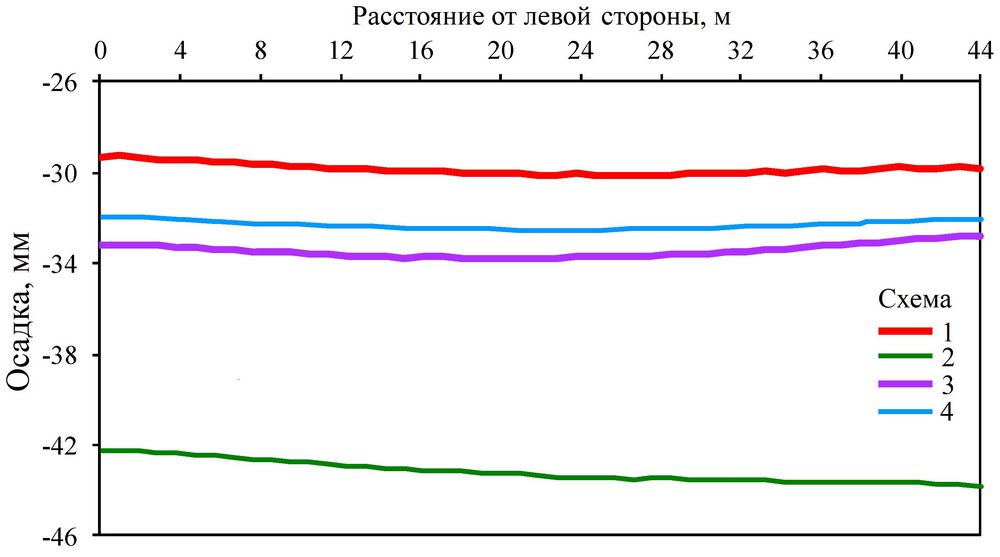
На рисунке 11 сопоставлены графики осадок фундаментной плиты вдоль ее продольного сечения, проходящего через ее середину, на основе четырех вышеописанных схем моделирования. Наибольшей по модулю была максимальная осадка для схемы 2 (S_max2 = -43,8 мм), наименьшей – для схемы 1 (S_max1 = -30,43 мм), а для схем 3 и 4 она была немного больше, чем для схемы 1. Из распределений осадок, показанных на рисунке 8, очевидно, что осадка S_max2 для схемы 2 произошла на правом конце плиты, а кривые осадок для трех других схем были распределены приблизительно симметрично (то есть максимальная осадка произошла около центра плиты). При этом распределения осадок плиты для четырех схем были достаточно равномерными. Различия между максимальными и минимальными осадками плиты для каждой схемы не превышали 2 мм (см. рис. 11).

Рис. 11. Кривые осадок фундаментной плиты вдоль ее продольного сечения, проходящего через ее середину, для четырех схем моделирования, описанных ранее в тексте

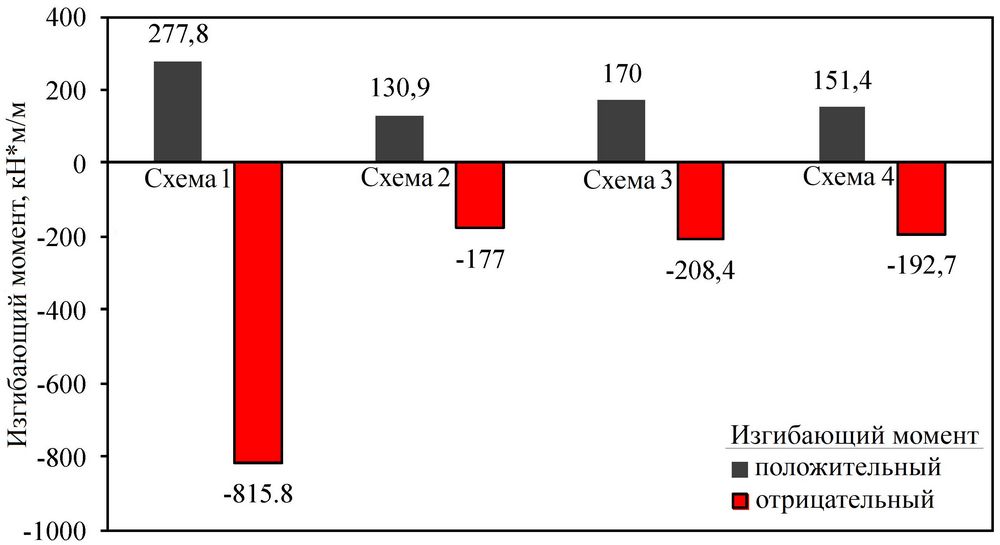
По схеме 1 бетонные буронабивные сваи жестко соединялись с плитой и осадки последней были наименьшими. Однако соединение между верхним концом сваи и плитой создавало относительно большой изгибающий момент. На рисунке 12 сопоставлены гистограммы экстремумов изгибающих моментов плиты для четырех расчетных схем. Отрицательный изгибающий момент для схемы 1 составил M_min1 = -815,8 кН*м/м, и этот экстремум был значительно больше по модулю, чем для трех других схем.

Рис. 12. Сопоставление экстремумов изгибающих моментов фундаментной плиты для четырех схем моделирования, описанных ранее в тексте

По схеме 2 между бетонной буронабивной сваей и плитой находилась грунтовая подушка. По сравнению с комбинированным фундаментом, усиленным сваями CFG по схеме 3, расстояние между соседними сваями по схеме 2 было большим, поэтому на каждую сваю приходилась более высокая нагрузка, несущая способность грунта между сваями была меньше – и это привело к большим деформациям сжатия. Поскольку жесткость бетонной буронабивной сваи была выше, чем у подушки и у грунта, подстилающего этот амортизирующий слой, то под действием нагрузки сверху верхние и нижние концы свай деформировались сильнее, что определенным образом сказалось на осадке плиты. В то же время экстремум изгибающего момента плиты значительно уменьшился по модулю, то есть M_min2 для схемы 2 был на 78,3% ниже, чем M_min1 для схемы 1.

По схеме 3, где использовались сваи CFG, осадка плиты была близка к таковой для схемы 4. Это говорит о том, что использование свай с относительно низкой прочностью и устройство грунтовой подушки соответствующей толщины между верхними концами свай и подошвой фундаментной плиты может оказать влияние на увеличение несущей способности грунта между сваями и хорошо контролировать осадки здания. В то же время изгибающий момент плиты фундамента был явно ниже, чем при жестком соединения верхних концов свай и плиты. Изгибающий момент фундаментной плиты M_min3 для схемы 3 был значительно (на 74,5%) ниже, чем M_min1 для схемы 1.

По схеме 4 для зоны, армированной сваями CFG, был применен эквивалентный интегральный метод (по которому, напомним, сваи для вертикального армирования и грунт рассматривались как анизотропное целое, параметры которого заменялись на эквивалентные параметрам армированной зоны. – Ред.). Разница между максимальными осадками для схем 4 и 3 составила примерно 3,8%. Разница между положительными и отрицательными изгибающими моментами для схем 4 и 3 составила 10,9 и  7,5% соответственно. Это указывает на то, что осадки и внутренние усилия, полученные с использованием эквивалентного интегрального метода обработки данных, были очень близки к осадкам и внутренним усилиям, которые были получены с использованием моделирования погруженных свай.

3.3.2. Поведение свай

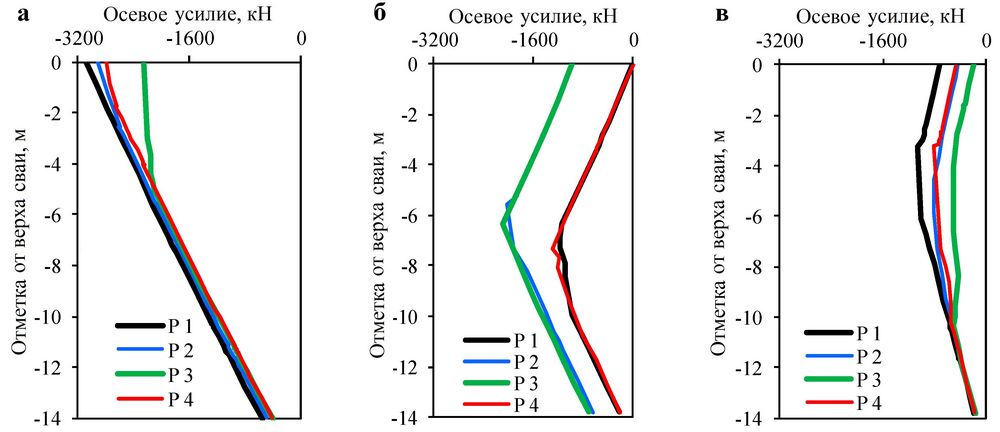
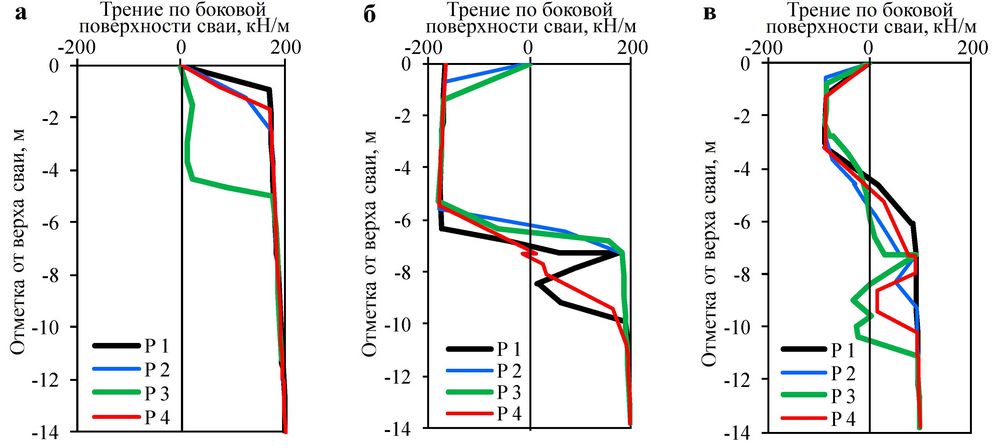
Для схем 1, 2 и 3 при моделировании свай использовались погруженные (1D) свайные элементы. Для этих трех схем были проанализированы осевые усилия и распределение трения по боковой поверхности свай P1–P4 (расположение этих свай показано на рисунке 4). Результаты выполненного анализа представлены на рисунках 13 и 14.

Из рисунка 13 видно, что распределения осевых усилий в сваях для разных схем моделирования (1, 2 и 3) были разными.

Для схемы 1 осевые усилия в сваях были больше вверху и меньше внизу, причем уменьшались с глубиной приблизительно линейно.

Для схемы 2 распределения осевых усилий были представлены ломаными линиями: в середине свай они были большими, а вверху и внизу – небольшими.

Для схемы 3 распределения осевых усилий в сваях имели приблизительно дугообразную форму: они были больше в определенном диапазоне средних и верхних частей свай, а примерно от четверти длины свай от верха до четверти их длины от низа осевые усилия изменялись по глубине приблизительно линейно. (Эти результаты согласуются с результатами анализа, представленными в статье [21].)

Распределения осевых усилий по длине разных свай (P1, P2, P3, P4 – см. рис. 4) для схемы 1 были похожими, хотя для центральной сваи (P3) было некоторое отличие по сравнению с боковыми (P2 и P4) и угловой (P1). Осевые усилия в свае P3 были больше от верха сваи до определенной глубины, а затем они линейно уменьшались с глубиной.

Для схемы 2 распределения осевых усилий по длине свай P1 и P4 были почти одинаковыми, для P2 и P3 они также были почти одинаковыми, причем для P1 и P4 они были выше, чем для P2 и P3.

Для схемы 3 осевые усилия в P1 были наибольшими, в P3 – наименьшими, а в P2 и P4 они находились между осевыми усилиями для P1 и P3, причем их распределения для P2 и P4 были практически одинаковыми.

Рис. 13. Распределение осевых усилий в сваях для схем моделирования 1 (а), 2 (б) и 3 (в), описанных в тексте ранее. Расположение свай P1–P4 показано на рисунке 4

На рисунке 14 показано распределение сил трения по боковой поверхности свай для тех же схем моделирования 1, 2 и 3. Для схемы 1 трение значительно отличалось от такового для схем 2 и 3. Для схемы 1 не было отрицательного трения по длине свай из-за синхронного оседания жестко связанных свай и плиты. Поскольку по схемам 2 и 3 между верхом свай и фундаментной плитой был амортизирующий слой определенной толщины, эта подушка была сжата и дала осадку под нагрузкой сверху, верхние концы свай вошли в нее, грунт между сваями сжался и деформировался под давлением от подушки и сваи сместились вниз. Следовательно, отрицательное трение появлялось в определенном диапазоне ниже верха свай для схем 2 и 3, а затем становилось положительным по мере увеличения глубины. Можно сделать вывод, что наличие подушки между верхом свай и фундаментной плитой определяет различия в механизмах взаимодействия «свая – грунт – плита» [21]. Кроме того, глубина распределения отрицательного трения по боковой поверхности свай для схемы 2 была близка к 6 м, что примерно в два раза превышало глубину распределения отрицательного трения для схемы 3. Это указывает на то, что относительное смещение между сваями и грунтом в основании фундаментной плиты, стабилизированном с помощью свай с высокой жесткостью, было больше, чем в случае  свай с относительно низкой жесткостью. С точки зрения механизмов взаимодействия «свая – грунт – подушка – плита» указанные выше причины также объясняют, почему осадка плиты для схемы 2 была больше.

Рис. 14. Распределение трения по боковой поверхности свай для схем моделирования 1 (а), 2 (б) и 3 (в), описанных в тексте ранее. Расположение свай P1–P4 показано на рисунке 4

4. ПРИМЕР ЧИСЛЕННЫХ РАСЧЕТОВ НА ОСНОВЕ СЛУЧАЯ ИЗ ПРАКТИКИ

Чтобы дополнительно проиллюстрировать пригодность метода эквивалентного моделирования, предложенного в этом исследовании, он был применен к конкретному строительному объекту в Пекине (Китай), где для целого комплекса зданий использовалась единая фундаментная плита. Под многоэтажными зданиями для армирования грунтового основания плиты использовались сваи CFG, а на участках наличия только подземных этажей и невысокого 3-этажного здания использовалось только естественное грунтовое основание под плитой.

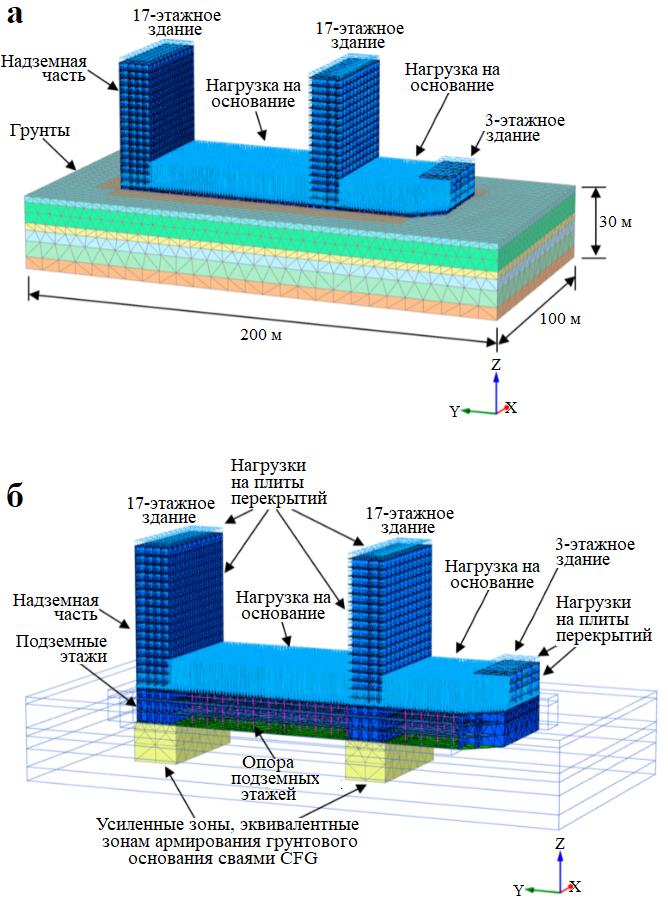
Моделирование в целом проводилось так же, как и в предыдущем разделе. Но для зон грунтового основания, армированных сваями CFG, использовалась в том числе замена на эквивалентный массив, когда каждая из этих зон рассматривалась как единое анизотропное целое с увеличенными параметрами прочности и жесткости по сравнению с обычным грунтовым основанием. Кроме того, чтобы учесть влияние жесткости надфундаментной части зданий на осадку плиты, была создана модель этой надфундаментной части с использованием плитных конечных элементов и были приложены нагрузки на перекрытия от каждого этажа по 15 кПа. Нагрузка на крышу подземного гаража составила 90 кПа.

Общий размер 3D-модели был 100 м x 200 м x 30 м (x x y x z), и она имела 73 437 десятиузловых тетраэдрических элементов, 162 202 узла, 41 675 плитных элементов, 450 балочных (стержневых) элементов и 1 698 интерфейсных элементов. На рисунке 15 в том числе показаны сетки 3D-моделей усиленных оснований фундаментной плиты под многоэтажными зданиями. Модельные параметры грунта приведены в таблице 1 (см. выше). Параметры балочных (стержневых) элементов опор подземных этажей: модуль упругости E = 3 x 10⁷ кПа, площадь поперечного сечения A = 0,36 м², момент инерции для площади поперечного сечения I = 0,01 м⁴. Параметры фундаментной плиты: толщина под высотными многоэтажными зданиями d = 0,8 м, толщина остальной части плиты d = 0,5 м, модуль упругости E = 3,25 x 10⁷ кПа. Параметры надземной части: толщина стенки d = 0,3 м, толщина перекрытий между этажами d = 0,2 м, модуль упругости перекрытий E = 3 x 10⁷ кПа. Эквивалентные параметры армированной зоны основания: модули упругости в горизонтальном и вертикальном направлениях – соответственно E₁ = 1,0 x 10⁴ кПа и E₂ = 1,2 x 10⁵ кПа; коэффициенты Пуассона в горизонтальном и вертикальном направлениях – соответственно ν₁ = ν₂ = 0,3; модуль сдвига в вертикальном направлении G₂ = 4,62 x 10⁴ кПа; удельное сцепление c = 270 кПа; угол внутреннего трения ϕ = 0 град.

Рис. 15. Интегральная сетка 3D-модели комплекса зданий и его основания (а); сетка 3D-модели надземной части, подземной части и усиленных зон основания фундаментной плиты под многоэтажными зданиями комплекса (б)

Процессы строительства моделировались следующим образом:

1) расчет начального поля напряжений;

2) выемка грунта под котлован для подземных этажей;

3) устройство свай CFG в виде эквивалентного массива;

4) строительство подземных этажей с учетом временной нагрузки на их кровлю;

5) строительство надземной части комплекса зданий путем приложения нагрузки на каждый этаж.

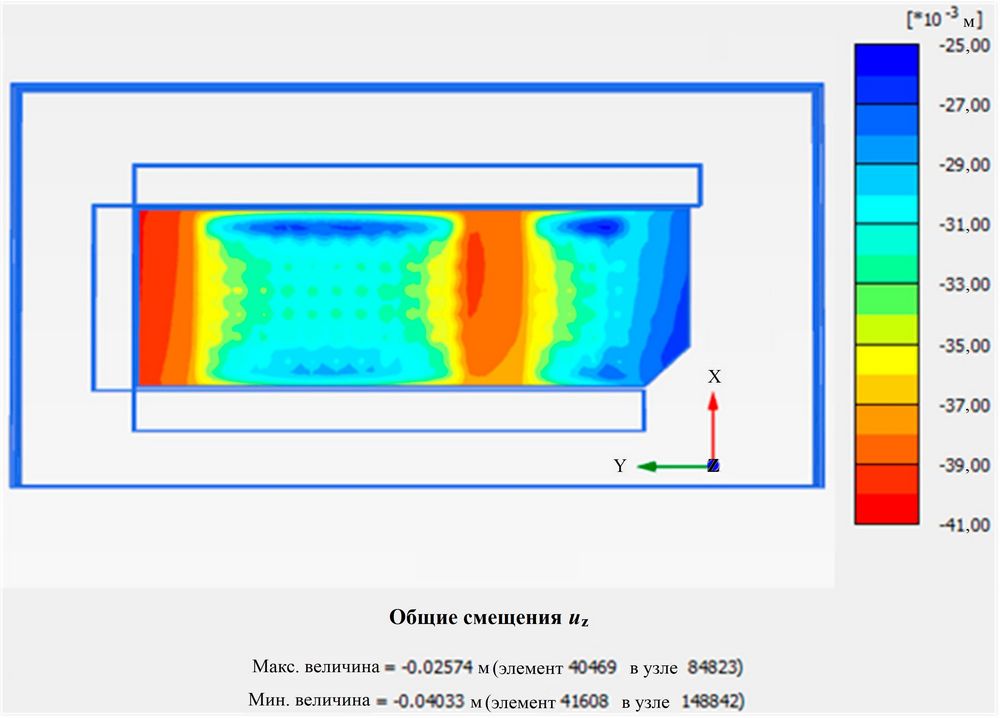
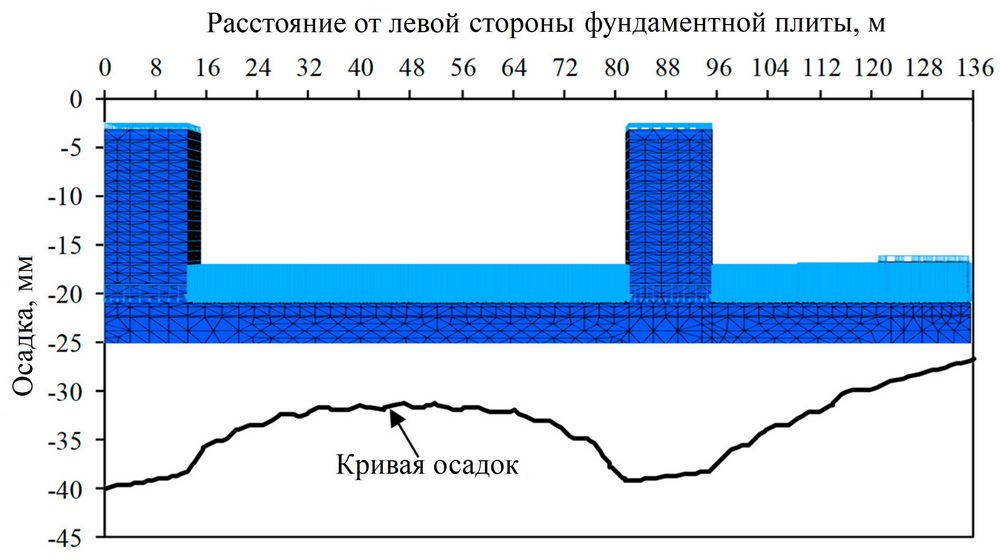
На рисунке 16 показано распределение осадок по всей фундаментной плите комплекса зданий в плане. На рисунке 17 представлено распределение осадок вдоль фундаментной плиты комплекса зданий на вертикальном разрезе, проходящем посередине многоэтажных домов и плиты. После армирования зон основания под многоэтажными зданиями сваями CFG осадки этих зданий составили около 40 мм. Максимальная осадка фундаментной плиты была 40,3 мм, а максимальная относительная осадка – примерно 0,5%, что ниже контрольного значения (2%) [28]. В соответствии с теоретическим методом, упомянутым выше, максимальная осадка фундаментной плиты составила 20,3 мм, а максимальная относительная осадка – 0,8%, что сходно с осадкой, полученной с помощью 3D численного моделирования, описанного в данном разделе. Эти результаты показывают, что осадки участков плит под многоэтажными зданиями, основания которых были армированы сваями CFG, а также осадки частей фундаментной плиты на естественном грунтовом основании (под подземными гаражами и трехэтажным зданием) соответствовали требованиям к осадкам.

Рис. 16. Распределение осадок по фундаментной плите комплекса зданий (вид в плане; красные и оранжевые цвета – под многоэтажными зданиями)

Рис. 17. Распределение осадок вдоль фундаментной плиты комплекса зданий (вертикальный разрез модели, проходящий посередине многоэтажных домов и плиты, и кривая осадок)

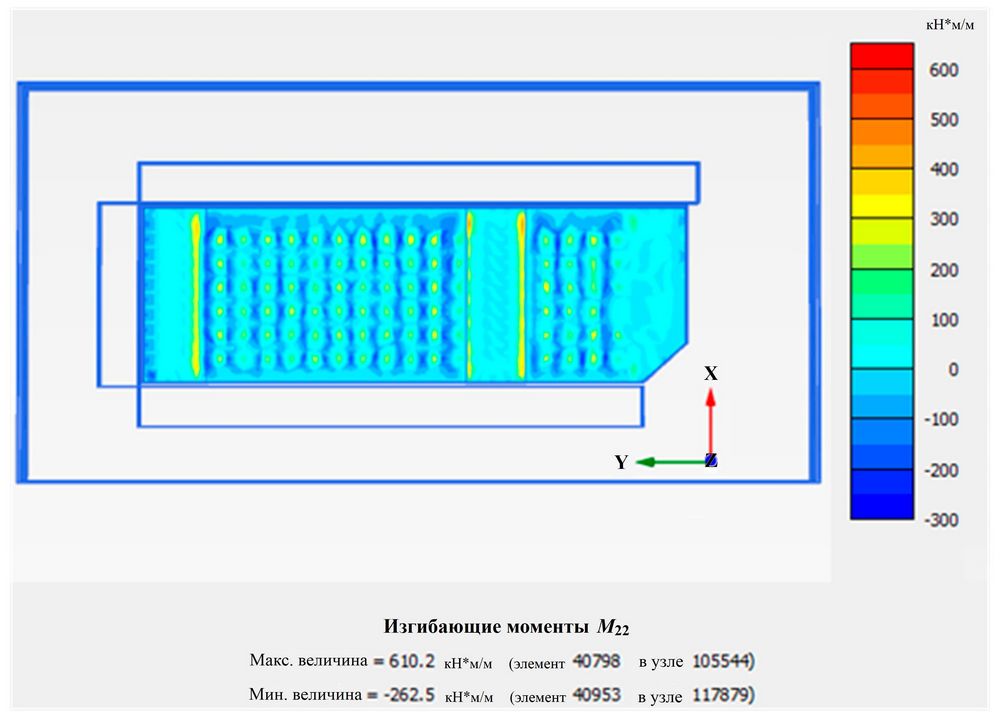
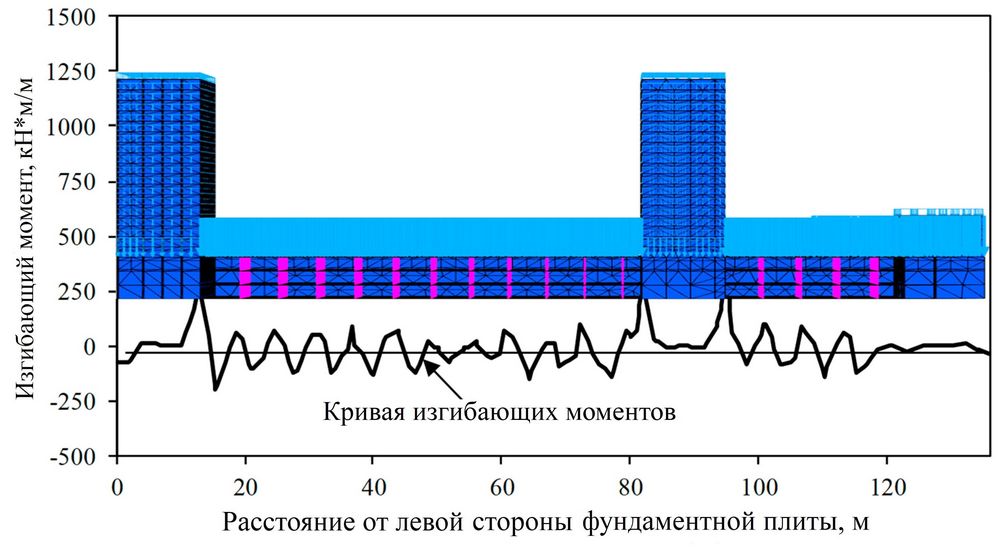
На рисунке 18 показано распределение изгибающих моментов по всей фундаментной плите комплекса зданий в плане. На рисунке 19 представлено распределение изгибающих моментов вдоль фундаментной плиты комплекса зданий на вертикальном разрезе, проходящем посередине многоэтажных домов и плиты. Как видно из этих рисунков, максимальная величина изгибающего момента составила 610,2 кН*м/м, а минимальная – минус 262,5 кН*м/м, а под многоэтажными зданиями распределение изгибающих моментов было достаточно равномерным. Это говорит о том, что с помощью предложенного метода моделирования, который является более экономичным для проектирования, могут быть получены приемлемые внутренние усилия в фундаментной плите. Более того, полученные численные результаты дают ориентир для расчетов внутренних усилий при проектировании конструкций фундаментной плиты.

Рис. 18. Распределение изгибающих моментов по фундаментной плите комплекса зданий (горизонтальный разрез через плиту)

Рис. 19. Распределение изгибающих моментов в фундаментной плите комплекса зданий (вертикальный разрез, проходящий посередине многоэтажных домов и плиты, и кривая изгибающих моментов).

5. ВЫВОДЫ

На основании расчетов и анализа, проведенных в данном исследовании, можно сделать следующие выводы.

1. В случае устройства подушки (амортизирующего слоя) между сваями и фундаментной плитой можно эффективно подобрать внутренние усилия в плите и уменьшить экстремумы изгибающих моментов. Однако, если прочность и жесткость свай высоки, общие осадки плиты могут увеличиться из-за больших деформаций в верхних и нижних частях свай.

2. Осадки можно хорошо снизить при усилении основания фундаментной плиты буронабивными сваями CFG с относительно низкой прочностью. Осевые усилия и изгибающие моменты в фундаментной плите при армировании ее основания сваями CFG в этом случае были явно ниже, чем при использовании бетонных буронабивных свай.

3. Когда количество свай очень велико, армированную ими зону грунтового основания можно рассматривать как единое тело из анизотропного упругопластического материала. После того как интегральные параметры прочности и жесткости этого материала были заданы должным образом, осадки и изгибающие моменты фундаментной плиты, полученные в модели с эквивалентной заменой свайного массива, стали более или менее близки к полученным при использовании метода моделирования погруженных свай (1D свайных элементов, погруженных в объемную грунтовую сетку).

4. Метод замены армированного сваями основания на эквивалентный грунтовый массив подходит для зданий большого размера с большим количеством несущих элементов и сложным взаимодействием между грунтом и конструкциями. Это эффективный и практичный метод быстрой оценки осадок при использовании различных схем устройства фундамента. Следует подчеркнуть, что выбор эквивалентных параметров для армированной зоны зависит от опыта инженера и выполненных пробных расчетов и требует систематического изучения в будущем.

-

Это исследование финансировалось Фондом естественных наук провинции Шаньси (201701D121068), Планом исследований Управления транспорта провинции Шаньси (2016-1-7), Китайским фондом постдокторантуры (2016M591044), Национальной программой фундаментальных исследований Китая (Программой 973, 2014CB047001) и Программой обучения инновациям и предпринимательству студентов в провинции Шаньси (201810108034) (Китай).

-

Авторы выражают благодарность Чжисяну Лю (Zhixiang Liu) из Китайского института проектирования и исследований строительных стандартов за его поддержку и помощь в численном моделировании.

Источник для адаптированного перевода

Niu X., Yao Y., Sun Y., He Y., Zhang H. 3D numerical analysis of synergetic interaction between high-rise building basement and cfg piles foundation // Applied Sciences. MDPI, 2018. Vol. 8. № 11. URL: mdpi.com/2076-3417/8/11/2040/htm.

Список литературы, использованной авторами переведенной статьи

1. Davis E.H., Poulos H.G. The analysis of piled raft systems // Aust. Geotech. J. 1972. Vol. 2. P. 21–27.
2. Giretti D. Modeling of piled raft foundations in sand: Ph.D. dissertation. Emilia-Romagna, Italy: University of Ferrara, 2010.
3. Wong I.H., Chang M.F., Cao X.D. Raft foundations with disconnected settlement-reducing piles // Design Applications of Raft Foundations (ed. by Hensley J.A.). London, UK: Tomas Telford, 2000. P. 154–196.
4. Li N., Han X. Numerical tests on the mechanism of the cushion in composite foundation // Rock Soil Mech. 2000. Vol. 21. P. 10–15.
5. Shahu J.T., Madhav M.R., Hayashi S. Analysis of soft ground-granular pile-granular mat system // Comput. Geotech. 2000. Vol. 27. P. 45–62.
6. He J., Hong B., Qiu G. Research on cushion action mechanism of CFG pile composite foundation for expressway // Rock Soil Mech. 2004. Vol. 25. P. 1663–1666.
7. Liang F., Li J., Chen L. Optimization of composite piled raft foundation with varied rigidity of cushion // Proceedings of the Sessions of the GeoShanghai Conference, Shanghai, China, 6–8 June 2006. Reston, VA, USA: American Society of Civil Engineers, 2006. P. 29–34.
8. Cao X.D., Wong I.H., Chang M.F. Behavior of model rafts resting on pile-reinforced sand // J. Geotech. Geoenviron. Eng. 2004. Vol. 130. P. 129–138.
9. El Sawwaf M. Experimental study of eccentrically loaded raft with connected and unconnected short piles // J. Geotech. Geoenviron. Eng. 2010. Vol. 136. P. 1394–1402.
10. Fioravante V., Giretti D. Contact versus noncontact piled raft foundations // Can. Geotech. J. 2010. Vol. 47. P. 1271–1287.
11. Fioravante V. Load transfer from a raft to a pile with an interposed layer // Geotechnique. 2011. Vol. 61. P. 121–132.
12. Rasouli H., Azizkandi A.S., Baziar M.H., Modarresi M., Shahnazari H. Centrifuge modeling of non-connected piled raft system // Int. J. Civ. Eng. 2015. Vol. 13. P. 114–123.
13. Zhu X.J. Analysis of the load sharing behaviour and cushion failure mode for a disconnected piled raft // Adv. Mater. Sci. Eng. 2017. Vol. 2017. Article ID 3856864. URL: hindawi.com/journals/amse/2017/3856864/.
14. Liu K., Xie X., Liu H. Performance of rigid-flexible-pile foundation with cushion // Proc. Inst. Civ. Eng. Geotech. Eng. 2010. Vol. 163. P. 221–227.
15. Zhang Z.M., Zhang Q.Q. Field test on composite foundation incorporating flexible and rigid piles // Adv. Mater. Res. 2011. Vol. 168–170. P. 1140–1144.
16. Liang F.Y., Chen L.Z., Shi X.G. Numerical analysis of composite piled raft with cushion subjected to vertical load // Comput. Geotech. 2003. Vol. 30. P. 443–453.
17. Zheng J.J., Abusharar S.W., Wang X.Z. Three-dimensional nonlinear finite element modeling of composite foundation formed by CFG lime piles // Comput. Geotech. 2008.Vol. 35. P. 637–643.
18. Sharma V.J., Vasanvala S.A., Solanki C.H. Behaviour of load-bearing components of a cushioned composite piled raft foundation under axial loading // Slovak J. Civ. Eng. 2014. Vol. 22. P. 25–34.
19. Tradigo F., Pisano F., Di Prisco C., Mussi A. Non-linear soil-structure interaction in disconnected piled raft foundations // Comput. Geotech. 2015, Vol. 63. P. 121–134.
20. Rasouli H., Ghalesari A.T., Modarresi M., Hasanzadeh A. Numerical study of non-contact piled raft interaction under static loads // Proceedings of the 5th International Conference on Civil Engineering and Urban Planning (CEUP2016), Xi’an, China, 23–26 August 2016 (ed/ by Mebarki A.). Beijing, China: World Scientific, 2017. P. 750–762.
21. Eslami A., Veiskarami M., Eslami M.M. Study on optimized piled-raft foundations (PRF) performance with connected and non-connected piles-three case histories // Int. J. Civ. Eng. 2012. Vol. 10. P. 100–111.
22. Ata A., Badrawi E., Nabil M. Numerical analysis of unconnected piled raft with cushion // Ain Shams Eng. J. 2015. Vol. 6. P. 421–428.
23. Sadek M., Shahrour I. A three-dimensional embedded beam element for reinforced geomaterials // Int. J. Numer. Anal. Methods Geomech. 2004. Vol. 28. P. 931–946.
24. Tschuchnigg F., Schweiger H.F. The embedded pile concept – verification of an efficient tool for modelling complex deep foundations // Comput. Geotech. 2015. Vol. 63. P. 244–254.
25. Tradigo F., Pisano F., di Prisco C. On the use of embedded pile elements for the numerical analysis of disconnected piled rafts // Comput. Geotech. 2016. Vol. 72. P. 89–99.
26. Zhao M.H., Zhang L., Yang M.H. Settlement calculation for long-short composite piled raft foundation // J. Cent. South Univ. Technol. 2006. Vol. 13. P. 749–754.
27. Zhang H., Shi M.L. Mechanical performance of settlement-reducing pile foundation with cushion // Adv  Mater. Res. 2012. Vol. 368. P. 2545–2549.
28. GB 50007-2011. Code for Design of Building Foundation. Beijing, China: Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Architecture & Building Press, 2011.
29. Goodman R.E., Taylor R.L., Brekke T.L. A model for the mechanics of jointed rock // J. Soil Mech. Found. Div. 1968. Vol. 94. P. 18–43.
30. Engin H.K., Septanika E.G., Brinkgreve R.B.J., Bonnier P.G. Modelling piled foundation by means of embedded piles // Proceedings of the 2nd International Workshop on Geotechnics of Soft Soils, Glasgow, Scotland, 3–5 September 2008. London, UK: Taylor & Francis Group, 2009. P. 131–139.
31. Mohammadinia A., Arulrajah A., Sanjayan J., Disfani M.M., Bo M.W., Darmawan S. Strength development and microfabric structure of construction and demolition aggregates stabilized with fly ash-based geopolymers // J. Mater. Civ. Eng. 2016. Vol. 28. Article 04016141.
32. Mohammadinia A., Arulrajah A., Horpibulsuk S., Chinkulkijniwat A. Effect of fly ash on properties of crushed brick and reclaimed asphalt in pavement base/subbase applications // J. Hazard. Mater. 2017. Vol. 321. P. 547–556.
33. JTG E40-2007 Test methods of soils for highway engineering. Beijing, China: Ministry of Transport of the People’s Republic of China, China Communications Press, 2007.