Моделирование и расчеты в PLAXIS. Осадки грунтов при строительстве систем из трех тоннелей с различной последовательностью проходки

Предлагаем вниманию читателей перевод статьи «Осадки грунтов при строительстве систем из трех тоннелей с различной последовательностью проходки», написанной сотрудниками факультета гражданского строительства Гентского университета (Бельгия) и опубликованной в 2019 году в журнале Advances in Civil Engineering («Достижения в гражданском строительстве»), выпускаемом научным издательством Hindawi. Эта статья находится в открытом доступе ) и распространяется по лицензии Creative Commons, которая разрешает ее неограниченное использование, распространение и воспроизведение при условии правильного цитирования оригинальной работы.
Объединение сечений двух или трех тоннелей, последовательно пройденных щитовым способом на небольших расстояниях друг от друга, в единое открытое поперечное сечение позволяет создать больше полезного внутритоннельного пространства, сохраняя при этом довольно компактную общую площадь сооружения. Однако такое объединение пройденных тоннельных выработок приводит к усложнению проектирования и строительства. Так, существующие методики оценки осадок охватывают только сооружение одиночного тоннеля или двух параллельных тоннелей. Представленное исследование направлено на расширение существующих методик для «многотоннельной геометрии». С помощью моделирования методом конечных элементов анализировалось поведение систем тоннелей при различных конфигурациях, расстояниях между тоннелями и последовательностях строительства. Для исследования относительных осадок при проходке тоннелей щитовым способом использовались комплексная геомеханическая модель упрочняющегося грунта при малых деформациях (HSS) и метод учета давления при нагнетании тампонажного раствора за обделку. Был сделан вывод, что оптимальной из рассмотренных в статье является тройная система при последовательности строительства тоннелей «верхний – левый – правый». По результатам моделирования это привело к уменьшению осадок на 36,9% и на 22,4% по сравнению соответственно с тройной системой при последовательности проходки «левый – правый – верхний» и с эквивалентной двойной системой в горизонтальной конфигурации при промежутке между тоннелями, равном трем их диаметрам.
Статья переведена при поддержке партнера журнала «ГеоИнфо» — компании «НИП-Информатика».

Насим Ахсан (Naseem Ahsan)
Докторант факультета гражданского строительства Гентского университета, Бельгия, ahsan.naseem@ugent.be
Шотт Кен (Schotte Ken)
Постдокторант факультета гражданского строительства Гентского университета, Бельгия
Де По Барт (De Pauw Bart)
Приглашенный профессор факультета гражданского строительства Гентского университета, Бельгия
Де Бакер Ханс (De Backer Hans)
Профессор факультета гражданского строительства Гентского университета, Бельгия
1. Введение
Из-за более высоких требований к трафику в городских районах многочисленные тоннели строятся ближе друг к другу в различных конфигурациях. При этом чаще всего предусматриваются транспортные системы из двух близко расположенных параллельных тоннелей, размещенных на одном горизонтальном уровне. В настоящее время также планируется создание тройных систем, в которых два тоннеля строятся рядом на одном горизонтальном уровне и третий сооружается над ними (либо на средней линии, либо под некоторым углом к ней). Но такая конфигурация приводит к чрезмерным осадкам в грунтовом массиве, которые могут вызвать повреждения соседних наземных и подземных сооружений. К факторам, способствующим этим осадкам, относятся: расстояние между тоннелями, их диаметр, порядок строительства и т.д.
Смещения земной поверхности и соответствующие им осадки в результате сооружения одиночных и сдвоенных тоннелей были предметом обширных исследований. Вышеупомянутые параметры были подробно изучены с помощью полевых измерений [1–6], лабораторных испытаний моделей [7–11] и численного моделирования [12–16].
Например, Пек [5] провел детальный анализ на основе полевых наблюдений и предложил метод определения осадок, вызванных строительством тоннелей, который позже был модифицирован для установления суммарных осадок при сооружении сдвоенных тоннелей.
Герцог [17] выполнил обширные испытания и предложил уравнение для определения максимальной осадки поверхности в результате строительства тоннеля.
Чапман и его коллеги [18] выделили следующие причины возникновения осадок, вызванных строительством тоннелей (и соответствующие типы осадок):
- из-за снятия напряжений во время выемки грунта;
- из-за работы тоннелепроходческого механизированного комплекса, или ТПМК (осадки, возникающие перед забоем, а также радиальные осадки вокруг оболочки ТПМК при его продвижении. – Ред.);
- из-за образования строительных зазоров и пустот между обделкой и грунтом (осадки в зоне хвостовой оболочки щита вследствие неполного заполнения строительного зазора тампонажным раствором. – Ред.);
- из-за включения грунта в работу при передаче нагрузок;
- из-за консолидации с течением времени (длительные осадки, развивающиеся после удаления ТПМК на значительное расстояние. – Ред.).
Мэйр [9] испытал на центрифуге модели тоннелей в глинах, чтобы определить осадки поверхности земли.
Также были проведены обширные исследования по двойным системам. Например, Адденбрук и Поттс [19] выполнили моделирование методом конечных элементов (МКЭ) для двух параллельных тоннелей в жестких глинах, рассмотрели консолидационные эффекты и изучили взаимодействия между этими тоннелями. Последнее является важным фактором, вносящим вклад в развитие осадок поверхности земли. Однако взаимодействие между тоннелями становится пренебрежимо малым, если разделяющее их расстояние превышает их диаметр в 7 раз.

При других исследованиях [2, 20] изучались различные формы мульд оседания, связанных с двойными системами, и в результате был разработан модифицированный метод оценки осадок.
Хант [21] исследовал влияние проходки нового тоннеля в непосредственной близости от уже созданных тоннелей, чтобы изучить, как влияет на осадки строительство на уже освоенных территориях по сравнению с новым строительством.
Чакери с соавторами [22] обнаружили, что если промежуток между двумя тоннелями превышает их диаметр в 3 раза, то осадки больше не зависят от их взаимодействия.
Чапман и его сотрудники [23] также провели аналогичные исследования и пришли к выводу, что чем больше промежуток между двумя близко расположенными тоннелями, тем меньше мульда оседания зависит от их взаимодействия.
Цю с соавторами [10] выполнили испытания на центрифуге для моделей двойных систем тоннелей в лёссовых грунтах с целью изучения деформаций поверхности.
Таким образом, анализ литературных источников позволяет объяснить поведение одиночных и сдвоенных тоннелей, а также их взаимодействия, но дает очень мало или совсем не дает сведений о взаимодействиях тоннелей в составе тройных систем (об их расположении и последовательности строительства, о результирующих осадках и т.д.) – соответственно, это также требует дальнейших исследований.
Настоящая работа включает подробный анализ предлагаемых тройных систем тоннелей, которые будут построены под Брюсселем для движения большого количества транспортных средств, с помощью программного комплекса PLAXIS 2D на основе метода конечных элементов. Выполнена оценка и представлено обсуждение разной геометрии размещения тоннелей, разных промежутков между ними и различной последовательности их проходки. И наконец, проанализированы мульды оседания для этих систем с использованием метода наложения и на этой основе определен оптимальный порядок строительства.
2. Описание проекта
Брюссель, будучи столицей, испытывает самые большие транспортные проблемы в Бельгии. Для решения этих проблем в настоящее время изучается вопрос о строительстве новой тоннельной хорды, призванной наладить перегруженное сообщение по рельсовым дорогам между севером и югом города (в Брюсселе имеются городские электрички, наземные и подземные трамваи, наземное и подземное метро, поэтому далее используются единые термины «рельсовые линии» и «рельсовые дороги». – Ред.). Этот проект включает строительство нескольких километров новых рельсовых линий, в том числе новых станций метро. Чтобы свести к минимуму нарушение повседневной жизни города, большая часть рельсовых путей будет находиться в тоннелях.
В рамках концептуального решения для этой новой тоннельной хорды в качестве обоснованной альтернативы традиционным методам тоннелестроения на участке между главными северными и центральными станциями рассматривается новаторская конструктивная схема, вмещающая четыре рельсовых пути, которая получается в результате объединения трех тоннелей, независимо пройденных щитовым способом (рис. 1).
![Рис. 1. Предлагаемая конфигурация тоннеля, полученного в результате объединения трех тоннелей, независимо пройденных щитовым способом (размеры приведены в сантиметрах) [24]](/images/dynamic/img43666.jpg)
Вместо создания двух или трех независимых тоннелей для размещения нескольких рельсовых путей и зон аварийной эвакуации тоннели объединяются в единое целое. Объединив сечения нескольких тоннелей, последовательно пройденных щитовым способом на очень небольшом расстоянии друг от друга, в одно открытое поперечное сечение, можно увеличить полезное пространство системы, сохранив при этом довольно компактную общую площадь сооружения. Это может быть ключевым преимуществом в условиях мегаполисов и больших городов, где рациональное использование доступного пространства под землей почти так же важно, как и на поверхности [24].
Однако такой подход приводит к усложнению процедуры строительства. Помимо технических трудностей, связанных с объединением независимых тоннелей, при их создании в городской среде основное внимание уделяется осадкам грунта, которые зависят от последовательности строительства и от расстояния между тоннелями. Но описанные в доступной литературе решения в основном ограничиваются расчетом мульд оседания для одиночного тоннеля и для систем из двух тоннелей.
3. Методика и последовательность исследования
Конфигурация тройной системы тоннелей была смоделирована в программном комплексе PLAXIS 2D, который обычно используется для геотехнического анализа, поскольку предоставляет широкий выбор комплексных геомеханических моделей грунта (параметры которых задаются по данным изысканий), в том числе таких как:
- модель слабого грунта (SSC);
- линейно-упругая модель (LE);
- модель Мора – Кулона (MC);
- модель упрочняющегося грунта (и модель упрочняющегося грунта при малых деформациях HS, HSS. – Ред.);
- модель «кэм-клэй» (Cam-Clay, CC);
- модифицированная модель «кэм-клэй» (MCC);
- упругопластическая модель.
Кроме того, PLAXIS 2D может учитывать нелинейное взаимодействие тоннеля и окружающих грунтов, упругопластическое поведение, а также сложность строительных операций.
Чтобы определить оптимальную конфигурацию тройных систем тоннелей, на основе доступной литературы и данных по второму Хейненордскому (Heinenoord) тоннелю была выбрана комплексная геомеханическая модель, которая хорошо аппроксимирует результаты полевых измерений. Затем с помощью моделирования определили оптимальную конфигурацию и оптимальную величину расстояния между сдвоенными тоннелями. После такого выбора смоделировали третий тоннель вместе с системой из двух тоннелей. Наконец, на основании полученных значений оседания поверхности были сделаны выводы.
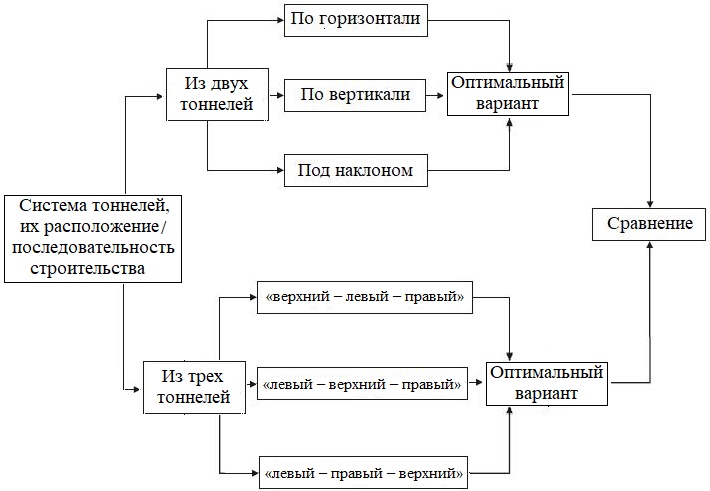
Подробная информация о системах тоннелей, смоделированных при этом исследовании, представлена в виде блок-схемы на рисунке 2.
4. Моделирование и графики осадок
4.1. Выбор комплексной геомеханической модели
Диас и Безуйен [25] выполнили подробный анализ для одиночного тоннеля диаметром 8 м, находящегося на глубине 30 м от поверхности земли, как показано на рисунке 3, а. Они сравнили модели: линейно-упругую (Linear Elastic – LE), Мора – Кулона (MC), Мора – Кулона с учетом дилатансии (MC.D), упрочняющегося грунта (Hardening Soil – HS) и упрочняющегося грунта при малых деформациях (HS small, HSS). На основании результатов своего исследования эти авторы сделали вывод, что модель MC завышает осадки, а наиболее подходящей является модель HSS, которая дает наиболее реалистичные величины осадок.
Мёллер и Вермеер [26] сравнили полевые данные для тоннеля диаметром 8,3 м, находящегося на глубине 16 м, с результатами использования моделей HS и HSS и заключили, что разница между осадками, полученными с помощью модели HSS и измеренными в полевых условиях, не превышает 20%, как показано на рисунке 3, б.
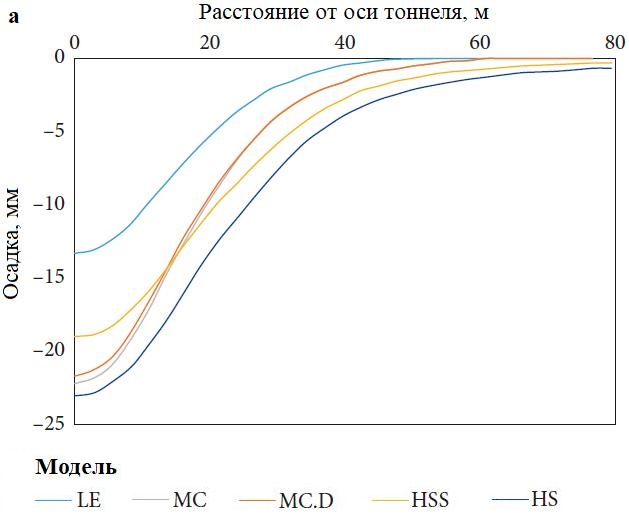
![Рис. 3. Сравнение осадок, полученных с помощью конститутивных (определяющих) моделей [25] и при полевых измерениях [26]](/images/dynamic/img43669.jpg)
Для структурного моделирования метод учета давления при нагнетании тампонажного раствора за обделку (grout pressure method) более реалистичен по сравнению с методом усадки (contraction method) и методом учета снимаемых напряжений (stress reduction method), поскольку он моделирует непосредственно сам метод строительства, позволяет получить точную ширину мульды оседания и значения внутренних усилий в конструкции наряду со смещениями (при моделировании тоннеля методом усадки реалистичные усилия в обделке и перемещения одновременно получить невозможно; внутренние усилия в обделке получают для состояния без усадки. – Ред.) [26, 27]. Поэтому проходка трех тоннелей моделировалась при настоящем исследовании с помощью модели HSS в сочетании с методом учета давления при нагнетании тампонажного раствора за обделку. При этом рассматривался метод учета умеренного давления нагнетания (self-composed grout pressure method), включающий в себя шесть промежуточных стадий (таблица 1). Принятая модель способна моделировать все стадии строительства при проходке тоннелей с помощью ТПМК [24]. Давление в забое [28, 29] и давление при нагнетании за хвостовую оболочку щита [30–32] были тщательно выбраны на основе существующих публикаций.
Таблица 1. Стадии строительства, использованные при моделировании в программе PLAXIS 2D [24]

4.2. Сравнение 2D- и 3D-моделирования
Для моделирования крупных и сложных тоннельных проектов лучше всего было бы применять трехмерный анализ. Но при этом требуются большие размеры моделей и значительные вычислительные затраты. Поэтому в настоящее время для повышения эффективности вычислений большинство исследователей все же использует двумерные альтернативы.
Мёллер [33] выполнил подробный анализ двумерных и трехмерных моделей HSS для получения мульды оседания для второго Хейненордского тоннеля. Он сделал вывод, что обе эти модели дали одинаковые мульды оседания в поперечном разрезе, и отметил, что 2D-моделирование работает достаточно хорошо, если применяются разумные давления на забой и на «хвостовую» поверхность.
4.3. Размеры сетки и граничные условия
Мейснер [34] рекомендовал обеспечивать расстояние от центра тоннеля до вертикальных границ сетки в 4–5 раз больше его диаметра и расстояние от центра тоннеля до нижней границы сетки в 2–3 раза больше его диаметра. Мёллер [33] же предложил следующее уравнение для расчета размеров сетки:
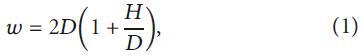
где w – ширина сетки, D – диаметр тоннеля, H – глубина от поверхности земли до свода тоннеля.
Размеры сетки для каждой конструктивной схемы тоннелей при настоящем исследовании рассчитывались с использованием обоих методов, но для моделирования выбирались более крупные размеры, чтобы избежать искажений и ошибок. Использовались 15-узловые треугольные элементы, при этом размер каждого элемента соответствовал 0,25 м для обеспечения более точных результатов расчета осадок грунта. Граничные условия были приняты вязкими для боковых границ, а верхняя граница считалась свободной, как было предложено в литературе для точного отражения деформационных явлений.
4.4. Валидация моделей
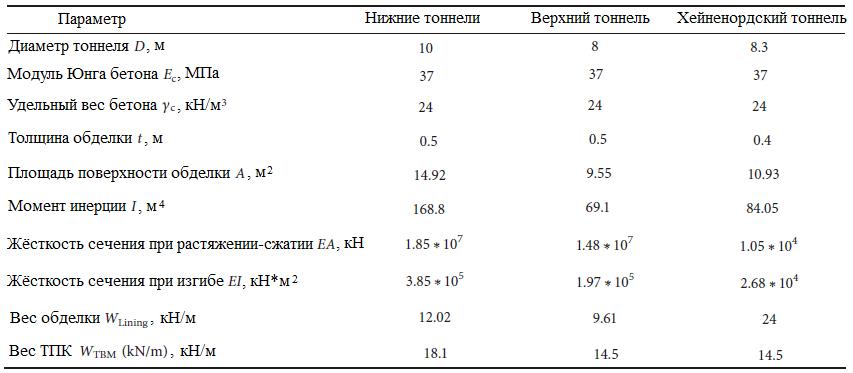
Также была выполнена валидация точности выбранных при данном исследовании комплексных геомеханических моделей, элементов конструкций и размеров элементов сетки путем сравнения с результатами полевых измерений для второго Хейненордского тоннеля, приведенными Мёллером [33]. Подробные параметры грунта, использованные при этой валидации, представлены в таблице 2, а параметры обделки – в таблице 3.
Таблица 2. Параметры грунта на площадке строительства второго Хейненордского тоннеля [33]
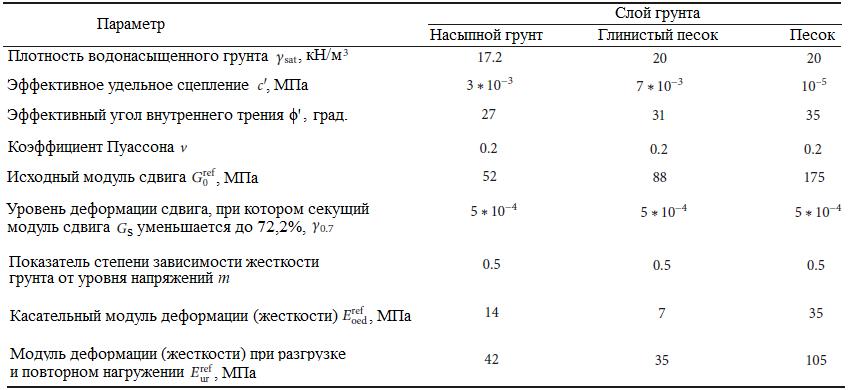
Таблица 3. Параметры обделки тоннелей [24]
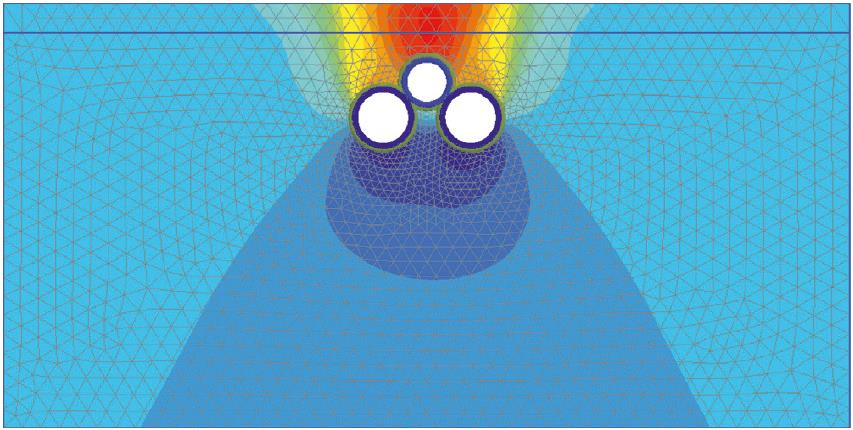
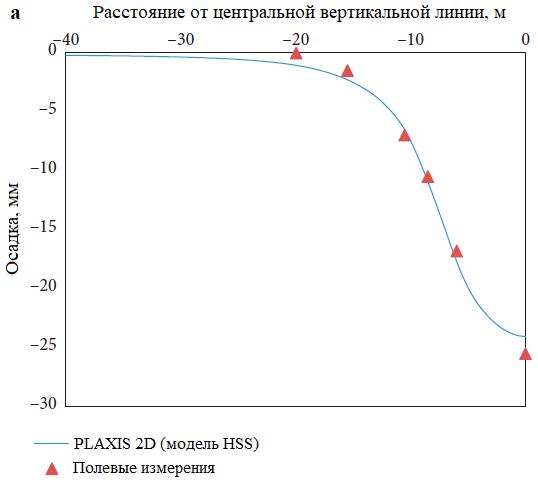
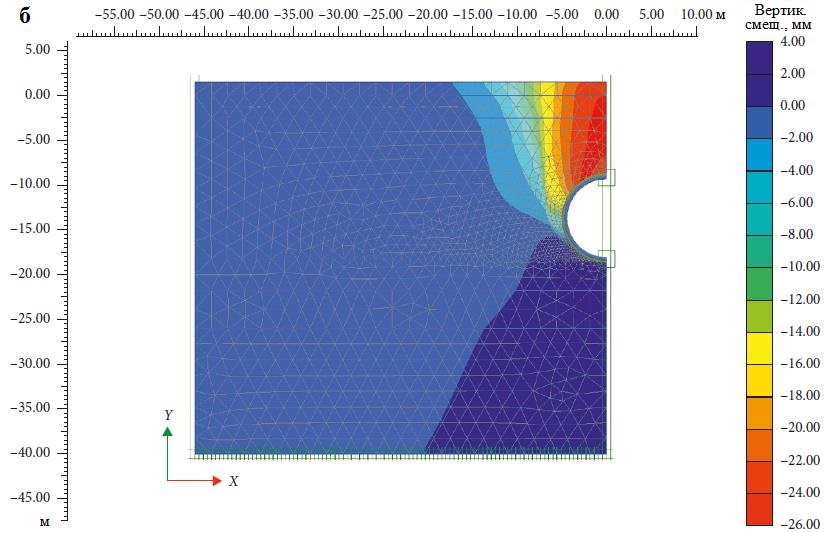
Сопоставление результатов компьютерного моделирования с полевыми данными и детальное представление вертикальных смещений грунта в изолиниях можно увидеть на рисунке 4. Из него видно, что результаты анализа с использованием метода конечных элементов хорошо согласуются с данными, полученными в полевых условиях, – с несущественной разницей, составляющей всего 1,4 мм (высокая степень достоверности моделирования связана с полными и достаточными исходными данными для модели HSS, учитывающей высокую жесткость при малых деформациях. – Ред.). Поэтому для всего исследования использовались одни и те же модели и размеры элементов сетки.
4.5. Свойства грунта и обделки тоннелей
Геологический разрез, использованный в настоящем исследовании, состоит из мощного слоя супеси (SC в соответствии с Единой системой классификации грунтов – USCS) с уровнем грунтовых вод (УГВ) на глубине 5 м от поверхности земли. Параметры грунта приведены в таблице 4.
Таблица 4. Параметры грунта на площадке строительства тоннелей по [24]

Обделка имеет толщину 0,5 м для тоннелей диаметром 8 м и 10 м. На основании этой толщины рассчитывались жесткость и другие параметры. Вес обделки рассчитывался на метр в плоскости поперечного сечения и на метр в продольном направлении относительно оси тоннеля. Для портала была принята плотность 260 кг/м3 [30], чтобы можно было рассчитать вес тоннелепроходческого комплекса. При этом ТПМК считался недеформируемым [24]. Характеристики материалов обделки тоннелей приведены в таблице 3.
5. Полученные результаты и их обсуждение
5.1. Конфигурации системы из двух тоннелей
Чтобы проверить правильность расположения тоннелей в выбранной тройной системе, сначала были смоделированы три конфигурации системы из двух тоннелей:
- горизонтальная (когда тоннели располагаются на одном уровне, то есть когда линия, проходящая через их центры в поперечном сечении, горизонтальна. – Ред.);
- вертикальная (когда линия, проходящая через центры тоннелей разного уровня, вертикальна. – Ред.);
- «скошенная» (когда линия, соединяющая центры тоннелей разного уровня, составляет с горизонталью 39 град. – Ред.).
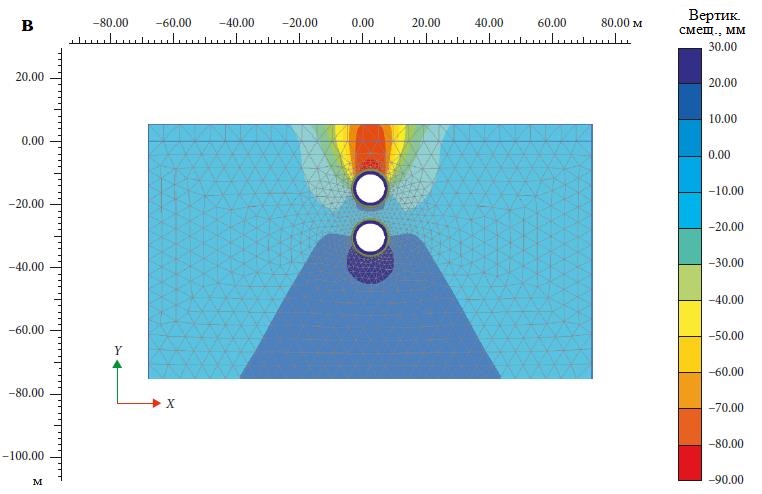
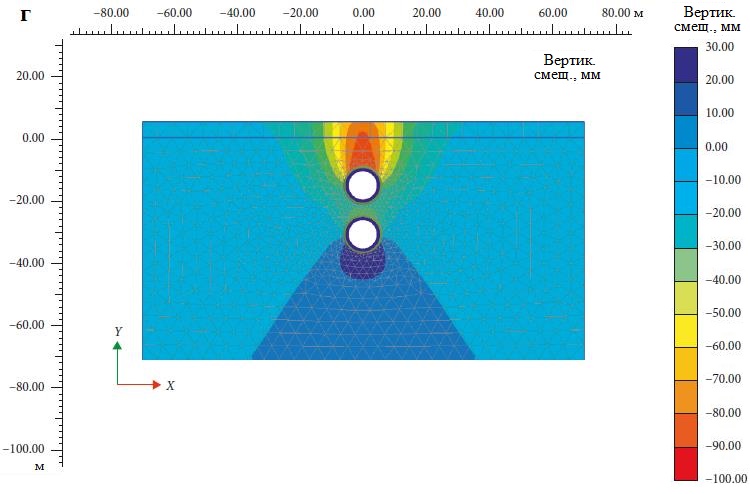
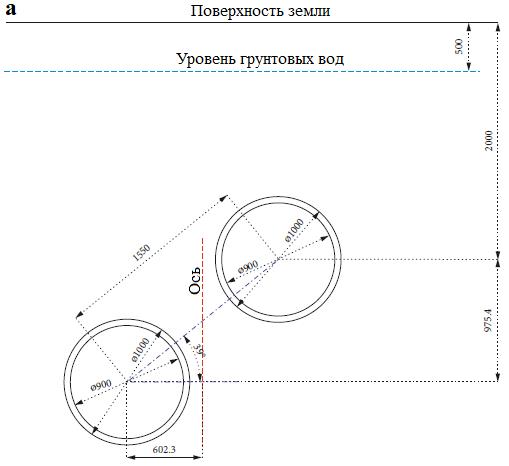
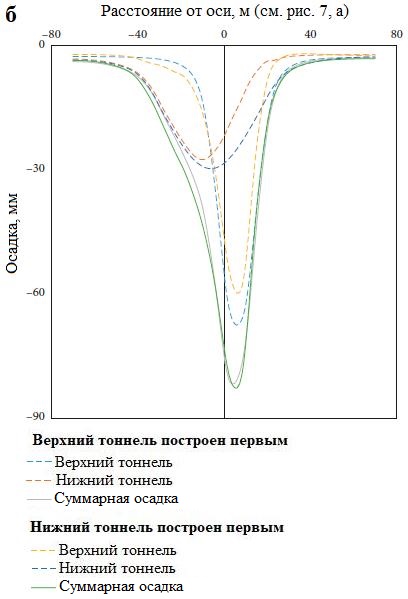
Эти три конфигурации показаны соответственно на рисунках 5, a; 6, a и 7, a. При этом вышеупомянутый угол 39 град. для «скошенной» конфигурации (см. рис. 7, а) был выбран для отражения того же наклона, что и для выбранной тройной системы (для линии, соединяющей центры того или другого нижнего тоннеля и верхнего тоннеля. – Ред.). Для всех трех вышеуказанных двойных систем были проанализированы осадки грунта. Рассматривалось также влияние величины промежутка между тоннелями.
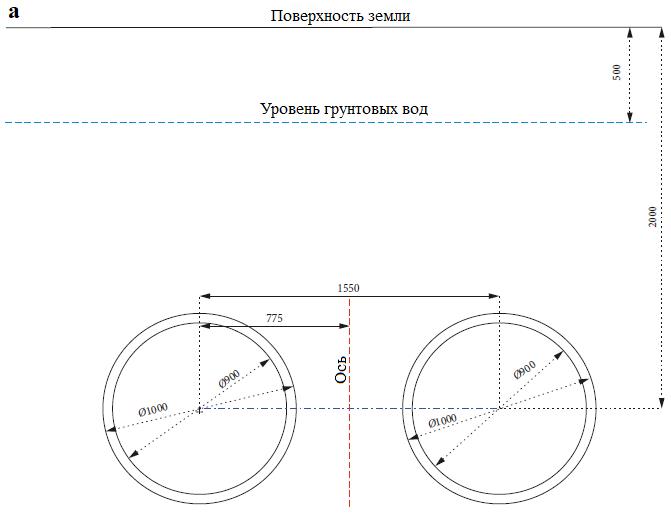
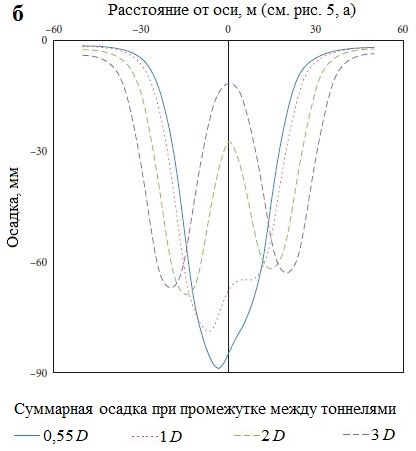
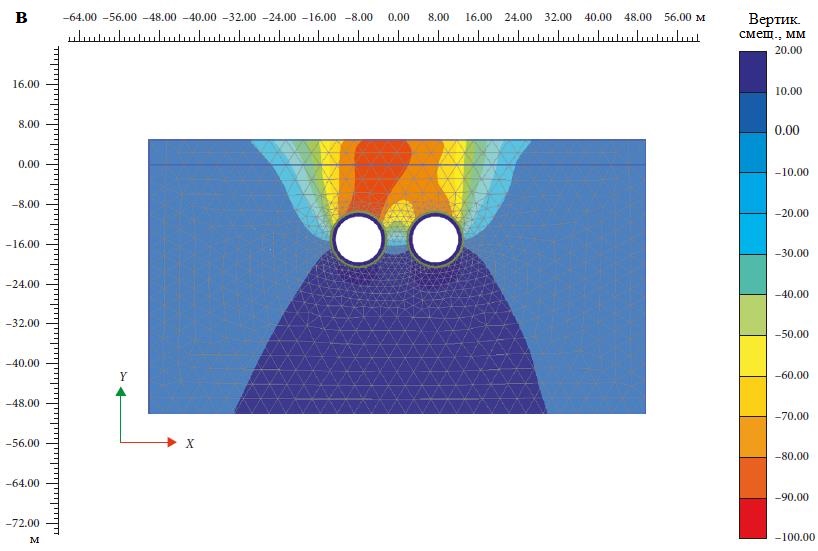
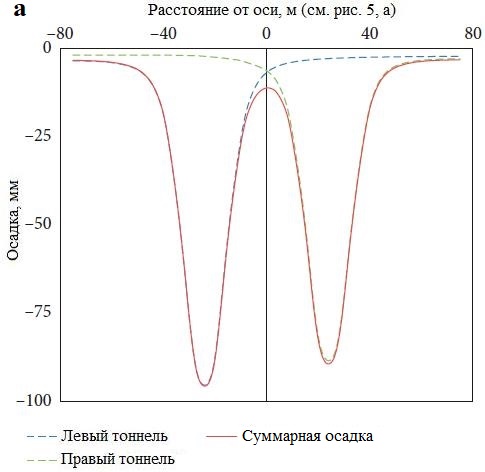
На рисунке 5, а показаны мульды оседания поверхности, а на рисунке 5, б детально представлены вертикальные смещения в грунтовом массиве в изолиниях для системы из двух тоннелей, размещенных в горизонтальной конфигурации. Из рисунка 5, б видно, что величина промежутка между тоннелями, равная 0,55D (где D – диаметр тоннелей), приводит к максимальному оседанию грунта, а по мере увеличения этого расстояния осадки уменьшаются. Моделирование также показало, что при дальнейшем увеличении промежутка от 2D до 3D разница в осадках составляет всего 2,5%. Причина заключается в том, что при 0,55D имеется большая перекрывающаяся зона сдвига между тоннелями, которая сужается от минимальной до нулевой по мере увеличения расстояния от 0,55D до 3D. Следовательно, можно сделать вывод, что при промежутке между тоннелями, превышающем 2D, эффект взаимодействия между ними пренебрежимо мал.
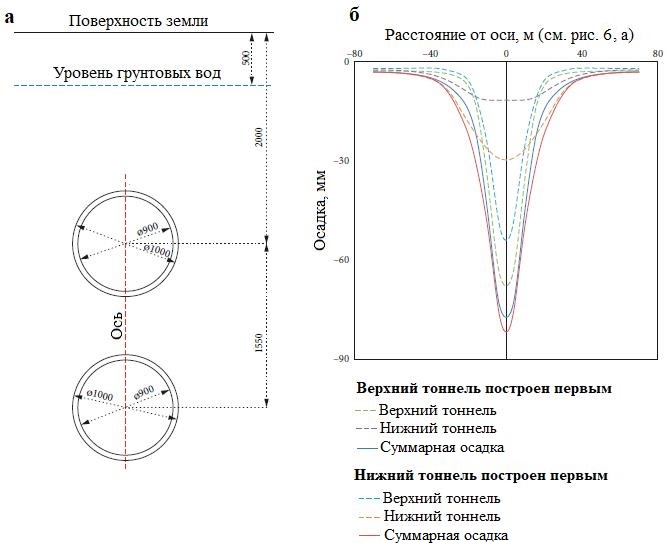
Из рисунка 6, б видно, что при вертикальной конфигурации системы из двух тоннелей важную роль играет последовательность строительства. Если верхний тоннель будет построен раньше нижнего, то осадки уменьшатся на 2,7%. Вертикальные смещения грунта в изолиниях для этой системы при разной последовательности проходки детально представлены на рисунках 6, в и 6, г.
Если тоннели размещены в «скошенной» конфигурации (если линия, соединяющая центры тоннелей в поперечном сечении, проходит под углом 39 град. к горизонтали), то строительство верхнего тоннеля первым приводит к осадкам, которые на 1,25% меньше по сравнению со случаем проходки сначала нижнего тоннеля (рис. 7, б). Вертикальные смещения в грунтовом массиве в изолиниях для этой системы при разной последовательности проходки детально представлены на рисунках 7, в, г.
В таблице 5 сопоставлены осадки для каждой из трех рассматриваемых конфигураций системы из двух тоннелей при величине промежутка между ними 0,55D. Из полученных результатов можно сделать вывод, что горизонтальная конфигурация приводит к осадкам, которые почти на 8,5% больше таковых при вертикальном и «скошенном» расположении тоннелей (последние две конфигурации дают более или менее одинаковые осадки).
Таблица 5. Максимальные осадки при разных конфигурациях и последовательностях строительства систем из двух тоннелей

5.2. Конфигурация системы из трех тоннелей
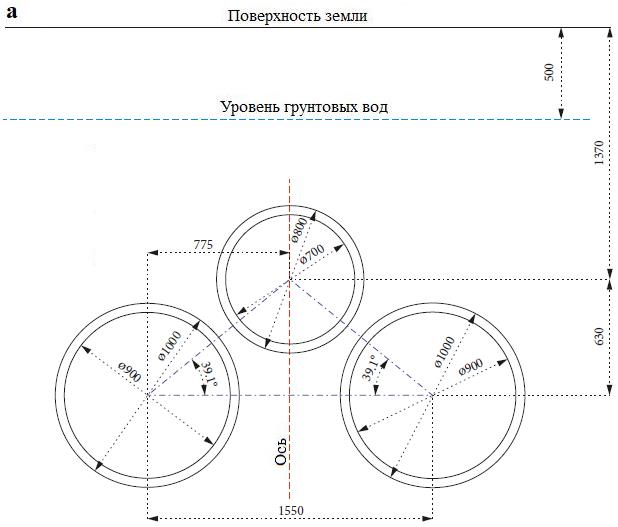
После определения оптимальной конфигурации системы из двух тоннелей была исследована тройная система, показанная на рисунке 8, а, чтобы определить оптимальную последовательность ее строительства.
При этом были смоделированы случаи для трех различных последовательностей строительства: когда верхний тоннель был пройден либо первым, либо вторым, либо последним. Для каждого из этих случаев были получены изолинии и графики осадок, для которых также было выполнено сравнение с таковыми для эквивалентной системы из двух тоннелей в горизонтальной конфигурации (которая может рассматриваться в качестве альтернативы для размещения тех же четырех рельсовых путей). Рассмотрим это подробнее.
5.2.1. Последовательность строительства тоннелей «верхний – левый – правый»
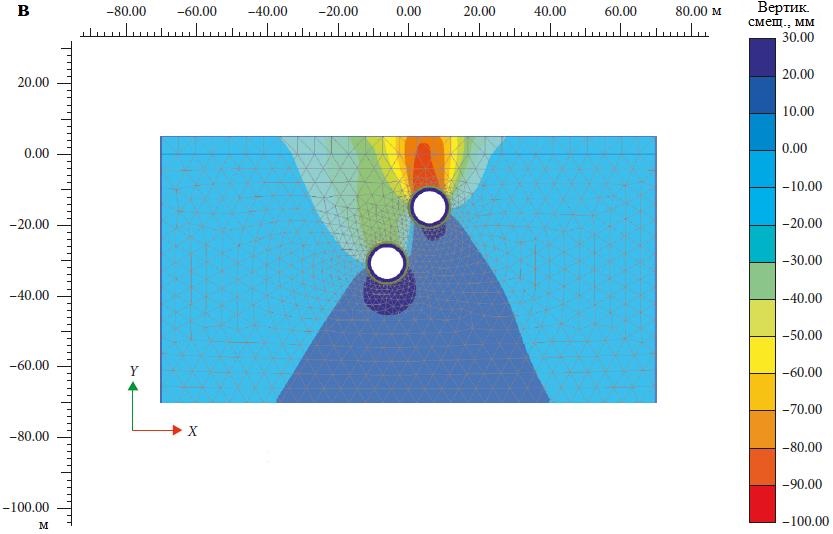
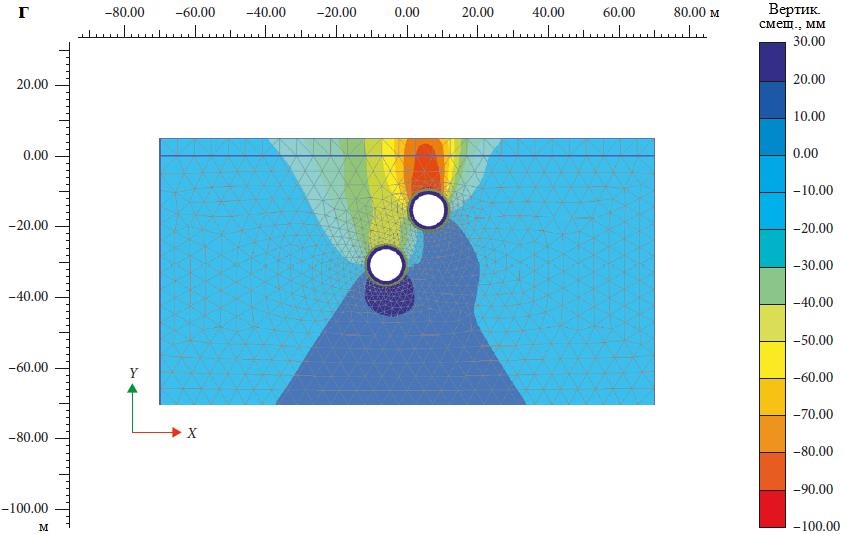
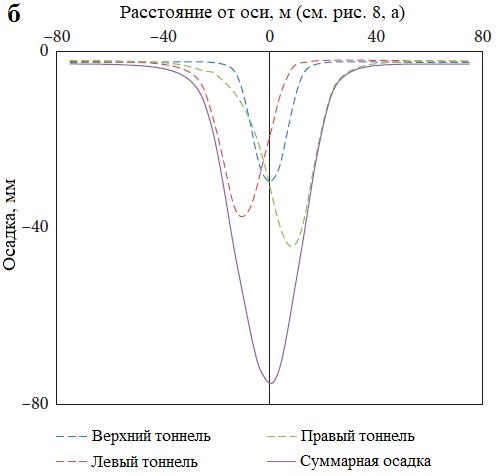
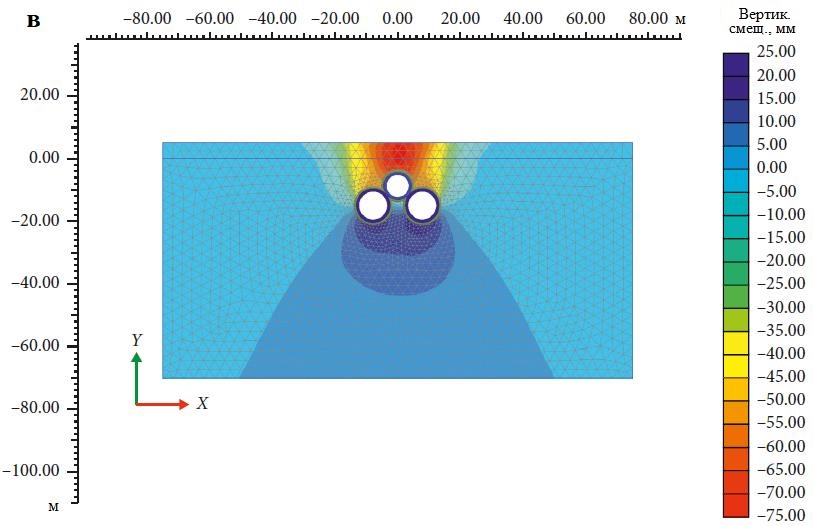
При таком подходе сначала строится верхний тоннель, потом левый, а затем правый. На рисунке 8, б показаны отдельные мульды оседания поверхности земли для каждого из этих тоннелей, а также суммарная мульда оседания, а на рисунке 8, в детально представлены осадки в грунтовом массиве в изолиниях. Из рисунка 8, б видно, что максимальная суммарная осадка грунта в результате строительства всех трех тоннелей составляет 75 мм.
5.2.2. Последовательность строительства тоннелей «левый – верхний – правый»
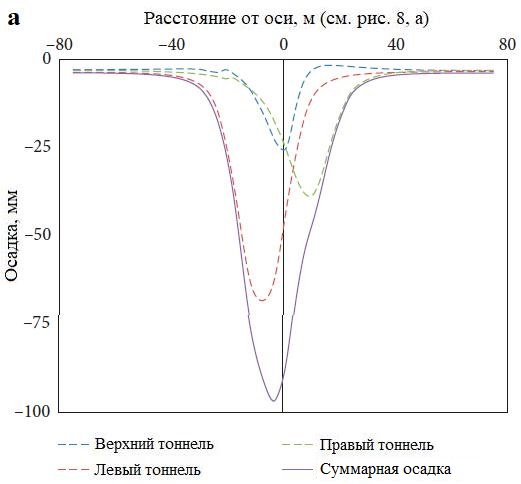
При таком подходе верхний тоннель строится сразу после завершения проходки левого нижнего, а в конце следует строительство правого тоннеля. На рисунке 9, a показаны отдельные мульды оседания поверхности земли для каждого из тоннелей, а также суммарная мульда оседания, а на рисунке 9, б детально представлены вертикальные смещения в грунтовом массиве в изолиниях. Из рисунка 9, а видно, что максимальная кумулятивная осадка грунта в результате строительства верхнего тоннеля тройной системы вторым составляет 98,75 мм, что почти на 32% больше осадки в случае строительства верхнего тоннеля первым. Мульда оседания верхнего тоннеля для последовательности проходки «левый – верхний – правый» также показывает выпор грунта на величину около 1,3 мм.
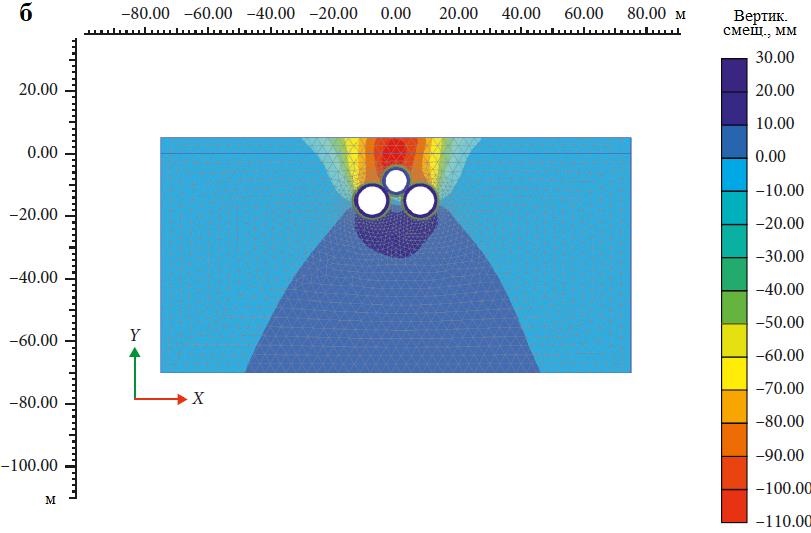
5.2.3. Последовательность строительства тоннелей «левый – правый – верхний»
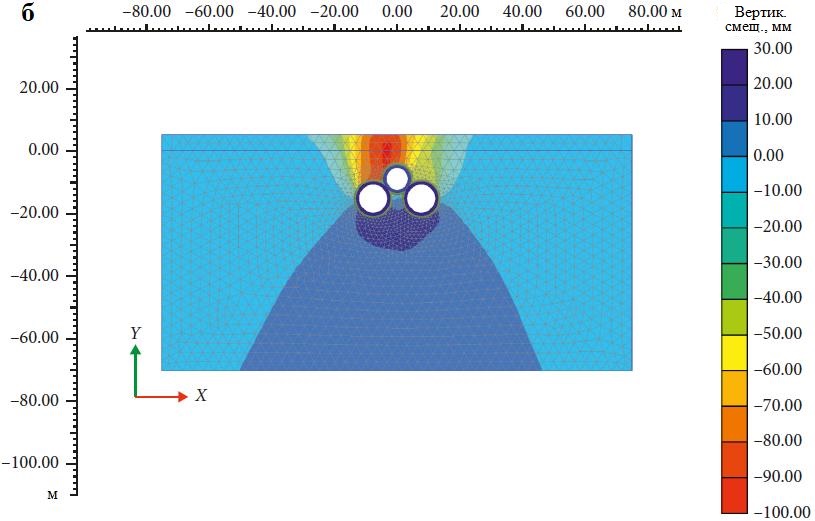
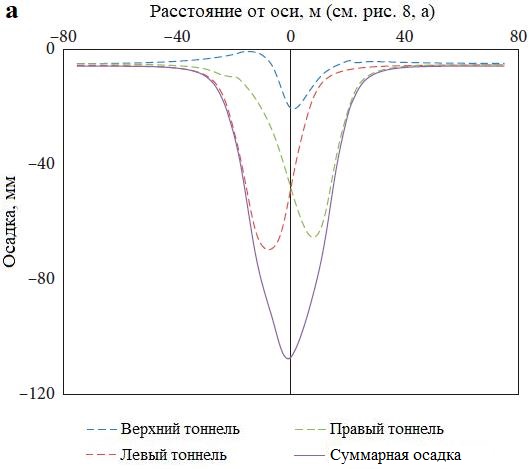
При таком подходе сначала сооружаются нижние тоннели, а в конце – верхний. На рисунке 10, a показаны отдельные мульды оседания для каждого из тоннелей, а также суммарная мульда оседания, а на рисунке 10, б детально представлены вертикальные смещения в грунтовом массиве в изолиниях. Из рисунка 10, а видно, что максимальная суммарная осадка при строительстве тройной системы тоннелей составляет 107 мм, что более чем на 8% и на 43% больше осадки в результате строительства верхнего тоннеля вторым и первым соответственно. Также можно заметить, что происходит выпор грунта примерно на 4,3 мм, что является существенной величиной и может вызвать проблемы для находящихся поблизости сооружений и фундаментов. Причина заключается в том, что после проходки нижних тоннелей в результате нагнетания цементного раствора окружающий грунт консолидируется, поэтому проходка верхнего тоннеля и создание его обделки вызовут на поверхности небольшой выпор грунта.
5.3. Эквивалентная система из двух тоннелей в горизонтальной конфигурации
Если вместо тройной системы тоннелей предусмотрена сдвоенная для размещения того же количества (четырех) рельсовых путей, потребуются тоннели большего размера. Их диаметр можно рассчитать по следующей формуле:
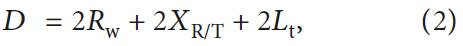
где Rw – ширина рельсового пути; XR/T – расстояние по горизонтали между рельсовым путем и стенкой (обделкой) тоннеля; Lt – толщина обделки.
Подставив в эту формулу Rw = 4,03 м: XR/T = 0,85 м и Lt = 0,5 м (см. рис. 1), получим, что диаметр D каждого тоннеля должен быть приблизительно равен 11 м. Величина промежутка между тоннелями для анализа была принята равной 3D.
На рисунке 11, a показаны отдельные мульды оседания для каждого из двух тоннелей, а также суммарная мульда оседания, а на рисунке 11, б детально представлены вертикальные смещения в грунтовом массиве в изолиниях.
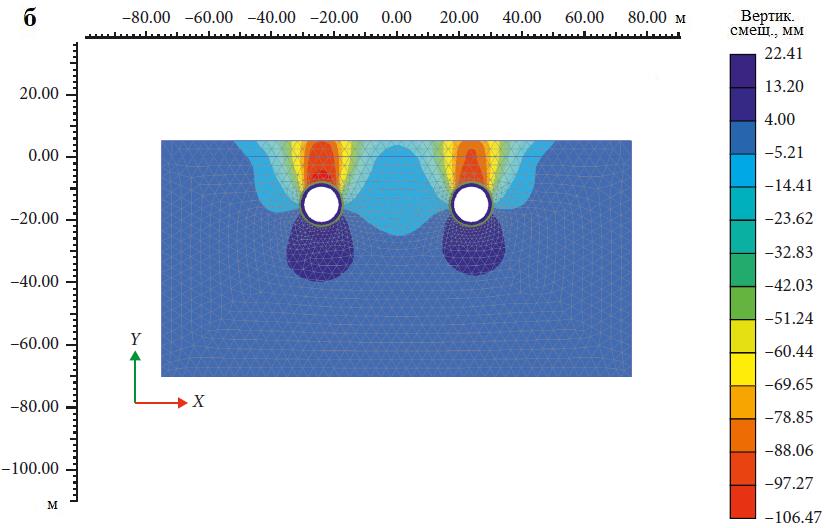
5.4. Сравнение результатов моделирования для системы из двух тоннелей в горизонтальной конфигурации и для рассмотренной тройной системы
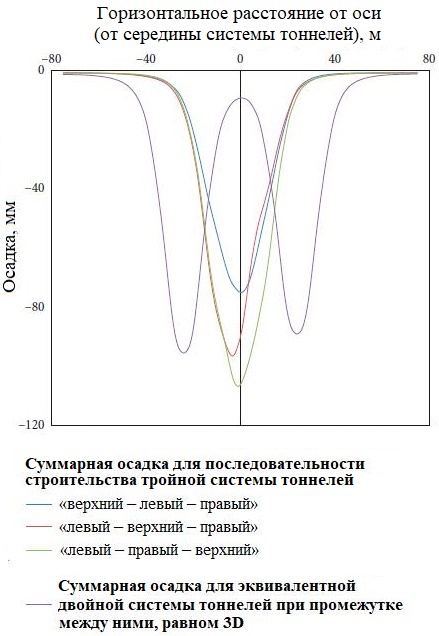
Мульды оседания для системы из трех тоннелей, представленные на рисунке 12, ясно показывают, что создание верхнего тоннеля последним приводит к самым большим осадкам, а также к выпору грунта. Последовательность строительства тоннелей «левый – верхний – правый» приводит к очень незначительному выпору грунта и при этом к почти таким же осадкам, как и для эквивалентной двойной системы в горизонтальной конфигурации. Последовательность «верхний – левый – правый» дает наименьшие осадки и почти полное отсутствие выпора. Строительство эквивалентной двойной системы в горизонтальной конфигурации (даже если промежуток между тоннелями равен 3D) приводит к осадкам, которые на 18,3% больше таковых для тройной системы при последовательности строительства «верхний – левый – правый» и почти идентичны осадкам для последовательности «левый – верхний – правый». Для меньших расстояний между тоннелями, которые часто предпочтительны или требуются в реальных ситуациях, эквивалентные двойные системы дадут осадки, еще больше отличающиеся от таковых для систем из трех тоннелей (см. рис. 5, б).
5.5. Обсуждение
В этой статье рассмотрен новый подход к строительству тоннелей с помощью двумерного численного моделирования в PLAXIS, которое предоставило детальное понимание схем деформации, возникающих в зависимости от различного размещения тоннелей в их двойных или тройных системах и от последовательности строительства. Для более точного определения деформаций исследование охватило все возможные этапы строительства тоннелей: проходку с помощью ТПМК, создание давления в забое, нагнетание тампонажного раствора за обделку и окончательное устройство обделки. Полученные результаты дали очень хорошую основу для сравнения поведения систем тоннелей в зависимости от схем их расположения и последовательности строительства. Однако понятно, что 2D-моделирование может охватывать только поперечные относительно оси тоннеля деформации. Хотя последние являются наиболее важными, для того чтобы лучше понять поведение систем тоннелей в продольном направлении, в будущем следует его изучить также с помощью 3D-моделирования, включая влияние равномерности и неравномерности зазора между проходческим щитом и грунтом, поскольку это не входило в объем данного исследования. Это позволит дополнительно уточнить полученные мульды оседания для различных сценариев.
6. Выводы
Главная цель этой работы состояла в том, чтобы исследовать оптимальную последовательность строительства системы из трех тоннелей, которая приводит к наименьшим осадкам при удовлетворении требований по обеспечению очень интенсивного трафика.
Из полученных результатов можно сделать следующие выводы.
1. Система из двух тоннелей в горизонтальной конфигурации (когда соединяющая их центры линия является горизонтальной) дает самые большие осадки по сравнению со всеми другими конфигурациями двойных систем.
2. Взаимодействие между тоннелями двойной системы в горизонтальной конфигурации, пройденными в супеси (SC в соответствии с системой классификации грунтов USCS), оказывает пренебрежимо малое влияние на осадки, если промежуток между тоннелями превышает 3D (где D – диаметр тоннелей).
3. Для системы из трех тоннелей очень важную роль в отношении влияния на осадки играет последовательность строительства. Чем раньше по отношению к остальным будет построен верхний тоннель, тем меньше будут осадки грунта.
4. Осадки для тройной системы тоннелей при последовательности строительства «верхний – левый – правый» примерно на 36,9% меньше, чем для последовательности «левый – правый – верхний», и на 22,4% меньше, чем для эквивалентной двойной системы с горизонтальной конфигурацией при промежутке между тоннелями, равном 3D.
7. Что предстоит сделать
Выполненное исследование позволило получить подробные сведения о схемах деформации рассмотренных систем при разном расположении тоннелей и разной последовательности их строительства. Но поскольку при этом использовался только 2D-анализ, рекомендуется также выполнить 3D-анализ, чтобы получить более хорошее и точное представление об общих деформациях, вызванных созданием таких систем тоннелей.
Доступность данных
Ничьи другие данные не использовались для поддержки этого исследования.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарность
Авторы хотели бы поблагодарить Стайна Ван Хоя (Stijn Van Hoye) за его вклад в настоящее исследование в рамках его дипломной работы магистра в Гентском университете.
Источник для перевода
Naseem A., Schotte K., De Pauw B., De Backer H. Ground settlements due to construction of triplet tunnels with different construction arrangements // Advances in Civil Engineering. Hindawi, 2019. Vol. 2019. Article ID 8637837. 18 p. URL: hindawi.com/journals/ace/2019/8637837/.
Список литературы, использованной автором переведенной статьи
[1] P. Attewell and M. Hurrell, “Settlement development caused by tunnelling in soil,” Ground Engineering, vol. 18, no. 8, pp. 17–20, 1985.
[2] M.L. Cooper, D.N. Chapman, C.D.F. Rogers, and A.H.C. Chan, “Movements in the piccadilly line tunnels due to the heathrow express construction,” Geotechnique, vol. 52, no. 4, pp. 243–257, 2002.
[3] Y. Mahmutoglu, “Surface subsidence induced by twin subway tunnelling in soft ground conditions in Istanbul,” Bulletin of Engineering Geology and the Environment, vol. 70, no. 1, pp. 115–131, 2011.
[4] I. Ocak, “Environmental effects of tunnel excavation in soft and shallow ground with EPBM: the case of Istanbul,” Environmental Earth Sciences, vol. 59, no. 2, pp. 347–352, 2009.
[5] R.B. Peck, “Deep excavations and tunneling in soft ground,” in Proceedings of 7th International Conference on Soil Mechanics & Foundation Engineering (SMFE), State of the Art, pp. 225–290, Mexico City, Mexico, July 1969.
[6] A. Saitoh, K. Gomi, and T. Shiraishi, “Influence forecast and field measurement of a tunnel excavation crossing right above existing tunnels,” International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, vol. 32, no. 3, p. A142, 1995.
[7] T. Kawata, M. Ohtsuka, and J. Reith, “Observational construction of large scaled twin road tunnels with minimum interval,” in Infrastructures Souterraines de Transports, Balkema, Rotterdam, Netherlands, 1993.
[8] R. Mair, “Geotechnical aspects of soft ground tunnelling,” in Proceedings of Conference on Construction Problems in Soft Soils, N.T.I., Singapore, December 1983.
[9] R.J. Mair, Centrifuge modelling of tunnel construction in soft clay, Ph.D. thesis, University of Cambridge, Cambridge, UK, 1979.
[10] J. Qiu, Y. Xie, H. Fan, Z. Wang, and Y. Zhang, “Centrifuge modelling of twin-tunnelling induced ground movements in loess strata,” Arabian Journal of Geosciences, vol. 10, no. 22, p. 493, 2017.
[11] R.N. Taylor, Ground movements associated with tunnels and trenches, Ph.D. thesis, Cambridge University, Cambridge, UK, 1979.
[12] A. Bobet, “Analytical solutions for shallow tunnels in saturated ground,” Journal of Engineering Mechanics, vol. 127, no. 12, pp. 1258–1266, 2001.
[13] K. Goshtasbi, A. Elyasi, and A. Naeimipour, “3D numerical stability analysis of multi-lateral well junctions,” Arabian Journal of Geosciences, vol. 6, no. 8, pp. 2981–2989, 2013.
[14] M. Karakus, A. Ozsan, and H. Basarэr, “Finite element analysis for the twin metro tunnel constructed in Ankara Clay, Turkey,” Bulletin of Engineering Geology and the Environment, vol. 66, no. 1, pp. 71–79, 2007.
[15] I. Shahrour and H. Mroueh, “Three-dimensional non linear analysis of a closely twin tunnels,” in Proceedings of Sixth International Symposium on Numerical Models in Geomechanics (NUMOG VI), pp. 481–487, Montreal, Canada, July 1997.
[16] E. Soliman, H. Duddeck, and H. Ahrens, “Two- and threedimensional analysis of closely spaced double-tube tunnels,” Tunnelling and Underground Space Technology, vol. 8, no. 1, pp. 13–18, 1993.
[17] M. Herzog, Die Setsungsmulde ЁUber Seicht Liegenden Tunneln, Vol. 11, Bautechnik, Berlin, Germany, 1985.
[18] D.N. Chapman, S.K. Ahn, D.V.L. Hunt, and A.H.C. Chan, “The use of model tests to investigate the ground displacements associated with multiple tunnel construction in soil,” Tunnelling and Underground Space Technology, vol. 21, no. 3- 4, p. 413, 2006.
[19] T.I. Addenbrooke and D.M. Potts, “Twin tunnel interaction: surface and subsurface effects,” International Journal of Geomechanics, vol. 1, no. 2, pp. 249–271, 2001.
[20] E.J. Cording, “Displacement around soft ground tunnelsgeneral report,” in Proceedings of 5th Pan-American Conference on Soil Mechanics and Foundation Engineering, Buenos Aires, Argentina, November 1975.
[21] D. Hunt, Predicting the Ground Movements above Twin Tunnels Constructed in London Clay, University of Birmingham Edgbaston, Birmingham, UK, 2005.
[22] H. Chakeri, Y. Ozcelik, and B. Unver, “Investigation of ground surface settlement in twin tunnels driven with EPBM in urban area,” Arabian Journal of Geosciences, vol. 8, no. 9, pp. 7655–7666, 2015.
[23] D.N. Chapman, S.K. Ahn, and D.V. Hunt, “Investigating ground movements caused by the construction of multiple tunnels in soft ground using laboratory model tests,” Canadian Geotechnical Journal, vol. 44, no. 6, pp. 631–643, 2007.
[24] K. Schotte, B. De Pauw, and H. De Backer, “Combining multiple independent shield driven tunnels: impact of construction order on surface settlements,” in Proceeding of ITA–AITES World Tunnel Congress, Dubai, UAE, April 2018.
[25] T. Dias and A. Bezuijen, “Tunnel modelling: stress release and constitutive aspects,” in Proceedings of 8th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground (IS-Seoul), CRC Press/Balkema, Seoul, South Korea, August 2014.
[26] S.C. Moller and P.A. Vermeer, “On numerical simulation of tunnel installation,” Tunnelling and Underground Space Technology, vol. 23, no. 4, pp. 461–475, 2008.
[27] K. Schikora and T. Fink, Berechnungsmethoden Moderner, Bergmannischer Bauweisen Beim U-Bahn-Bau Bauingenieur, vol. 57, pp. 193–198, 1982.
[28] W. Broere, Tunnel Face Stability & New CPT Applications, Delft University of Technology, Delft, Netherlands, 2001.
[29] V. Guglielmetti, P. Grasso, A. Mahtab, and S.Xu, Mechanized Tunnelling in Urban Areas: Design Methodology and Construction Control, CRC Press, Boca Raton, FL, USA, 2008.
[30] A. Bezuijen and A. Talmon, Grout Pressures around a Tunnel Lining, Influence of Grout Consolidation and Loading on Lining, Taylor & Francis/Balkema, Netherlands, 2004.
[31] J. Shirlaw, “Setting operating pressures for TBM tunnelling,” in Proceedings of the 32nd Geotechnical Division’s Annual Seminar, Hong Kong Institution of Engineers (HKIE), Hong Kong, May 2012.
[32] A. Talmon, L. Aanen, A. Bezuijen, and W. van der Zon, “Grout pressures around a tunnel lining,” in Tunnelling. A Decade of Progress. GeoDelft 1995–2005, pp. 77–82, Taylor & Francis/Balkema, Netherlands, 2006.
[33] S.C. Moller, Tunnel induced settlements and structural forces in linings, Ph.D. thesis, University of Stuttgart–Institute of Geotechnical Engineering, Stuttgart, Germany, 2006.
[34] H. Meisner, “Tunnelbau unter tage–empfehlungen des arbeitskreises 1.6 “Numerik in der geotechnik” abschnitt 2,” Geotechnik, vol. 19, no. 2, pp. 99–108, 1996.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц