О моделировании в PLAXIS 3D для оценки вибраций поверхности земли при движении поезда метро

Оценка влияния, или геотехнический прогноз, – одна из самых сложных и в то же время часто встречающихся задач при строительстве подземных сооружений в больших городах. Активность строительства метро, особенно в Москве, очень высока. Прокладка линий метро оказывает влияние на окружающую застройку – и поэтому проектные организации должны выполнять соответствующие подтверждающие расчеты.
Развитие механики грунтов и геотехнического программного обеспечения позволяет сегодня решать динамические задачи во все более сложных постановках с учетом различных особенностей поведения грунтов и способов приложения динамической нагрузки. В том числе разработчики программного комплекса PLAXIS активно совершенствуют его интерфейс в части улучшения и облегчения работы по созданию сложных расчетных схем, особенно для тоннелей. Например, в последней версии V21, которая вышла в конце января 2021 года, был существенно улучшен импорт геометрии тоннелей в двумерной и трехмерной постановках.
В качестве примера практического применения PLAXIS при решении подобных задач предлагаем вниманию читателей обзор материалов доклада «Трехмерное моделирование вибраций земной поверхности, вызванных движением поезда метро» [1] сделанного в 2016 году на 11-м Международном симпозиуме по теории пластичности и контактной механике (Implast 2016). Его авторы Д.В. Сингх и Й. Сет на тот момент были выпускниками бакалавриата и будущими студентами магистратуры факультета гражданского строительства Индийского технологического института города Дели. Этот доклад был опубликован всемирно известным издательством Elsevier в журнале Procedia Engineering в 2017 году.
Сингх и Сет основали свою работу [1] на аналитическом решении для распределения воздействий колесных пар на рельсы по отношению к движущейся системе отсчета, которое в 2007 году выполнили Коррейя с соавторами (Correia et al.) в двумерной постановке. Индийские исследователи [1] использовали это распределение сил для анализа методом конечных элементов в программном комплексе PLAXIS 3D. В пакете прикладных программ MATLAB авторы доклада [1] разработали программу для формирования матрицы динамических коэффициентов для каждой статической точечной нагрузки, приложенной вдоль рельсового пути на каждом временном шаге. Величина приложенной нагрузки равна нагрузке от колесной пары на рельсы, полученной в результате решения задачи по изгибу балки на упругом основании Винклера при перемещении нагрузки. Полученные результаты могут быть использованы для оценки влияния изменений различных геологических и физических параметров на распределение сил при нагрузках от колесных пар. После калибровки по геотехническим и физическим данным, которые соответствуют участкам над реальными рельсовыми путями метро, полученную модель можно использовать для прогнозирования воздействия вибраций на существующую инфраструктуру.
Отметим, что в предлагаемом обзоре надписи на копиях рисунков не переводились на русский язык, поскольку это не позволено лицензией, по которой статья [1] находится в открытом доступе.
Обзор написан при поддержке и с комментариями сотрудников компании «НИП-Информатика» – партнера журнала «ГеоИнфо».
ВВЕДЕНИЕ
Быстро растущая численность населения требует все более эффективного общественного транспорта, в связи с чем значительно усилилось внимание прежде всего к метро. Однако строительство сетей подземного транспорта является наиболее сложным, особенно если они предназначены для интенсивного высокоскоростного движения.
При проектировании таких систем требуются обширные предварительные исследования, испытания и комплексный анализ с учетом динамического поведения грунтов. И здесь большое значение имеет правильное моделирование всей системы транспортного сооружения с учетом поведения рельсового пути, насыпных грунтов и окружающего грунтового массива, особенно при нагрузках от движущихся поездов метро.
Проблемы взаимодействия «грунт – сооружение» при проектировании рельсовых путей являются одними из самых сложных для анализа. Расчетные схемы при этом должны охватывать: многоосные нагрузки от множества колесных пар, различающиеся по величине и частоте; деформируемые рельсы, прикрепленные к деформируемым шпалам гибкими скреплениями; расстояние между шпалами, которое можно изменять; свойства и толщину балласта и земляного полотна (если они предусмотрены); свойства подстилающих слоев грунтового основания.

В связи с важностью и сложностью этих проблем Д.В. Сингх и Й. Сет с факультета гражданского строительства Индийского технологического института города Дели подготовили доклад «Трехмерное моделирование вибраций земной поверхности, вызванных движением поезда метро» [1] и выступили с ним в 2016 году на 11-м Международном симпозиуме по теории пластичности и контактной механике (Implast 2016).
Эта работа была опубликована всемирно известным издательством Elsevier в журнале Procedia Engineering в 2017 году. Здесь мы представляем краткий обзор материалов указанного исследования.
В начале своего доклада [1] Сингх и Сет подчеркнули, что воздействие подвижной нагрузки на слой грунта сильно отличается от влияния статической нагрузки и является гораздо менее изученным. Движущаяся нагрузка вызывает многократные нагружения и разгрузки для любого участка грунта под рельсовым путем и может привести к значительно большим смещениям в грунтовом массиве. Конечная общая неупругая деформация, возникающая в грунте, зависит от ряда параметров, а именно от характеристик грунта основания и подстилающих его слоев, неровностей пути, вибраций, вызванных движущимися поездами, приложенной нагрузки, частоты цикла «нагружение – разгрузка», характеристик насыпи и т.д. Хотя небольшие осадки железнодорожных путей и могут быть приемлемыми, очень часто наблюдаются неравномерные осадки – прежде всего из-за неоднородности слоев грунта и внешних факторов (например, приложенной нагрузки и т.д.). Эти неравномерные осадки в первую очередь бывают ответственны за расстройство рельсовой колеи.
Для быстро движущихся поездов требуются тщательный анализ и оценка неравномерных осадок, чтобы предотвратить их сход с рельсов. Также следует рассмотреть реакции грунтов на динамические нагрузки от быстро идущих поездов (динамические свойства грунтов). После определенной критической скорости, являющейся функцией слоев грунта, для оценки смещений необходимо учитывать коэффициент динамического усиления (dynamic amplification factor), умноженный на нагрузку. Однако Сингх и Сет в своей работе [1] рассмотрели поезда, идущие со скоростью ниже критической, что позволило им избежать необходимости использования коэффициента динамического усиления.
МОДЕЛИРОВАНИЕ
В своей работе [1] авторы провели исследования на трехмерной модели с использованием программного комплекса PLAXIS 3D в сочетании с расширением двумерной математической модели по динамическому анализу рельсового пути для высокоскоростных поездов, представленной в 2007 году Коррейя с соавторами (Correia et al.).
Математическая модель
Для расчетов Сингх и Сет [1] приняли условия плоской деформации. Поскольку точечная нагрузка в условиях плоского напряжения преобразуется в распределенную нагрузку в трехмерной модели, ее применимость ограничивают следующие упрощения и допущения, указанные в работе Гутовского с соавторами (Gutowski et al.) 1976 года.
1. Было принято, что действие линейной нагрузки ограничено расстоянием d = LT/π (где LT – максимальное расстояние между крайними осями). По сути, это означает, что результаты, полученные Коррейя с соавторами (Correia et al.) с использованием 2D-подхода, считались действительными до расстояния d.
2. Учитывалась реакция рельсового пути на приложение точечных нагрузок. В силу его жесткости приложенная точечная нагрузка ощущается как нагрузка, распределенная по нему. Как утверждали Коррейя с соавторами (Correia et al.), на которых ссылаются авторы доклада [1], точная форма кривой распределенной нагрузки (при скоростях ниже критической) будет функцией скорости движущейся нагрузки, но она принимает эту общую форму для всех скоростей, которые меньше критической. Экстремум такой кривой имеет тенденцию быть более узким (острым) для более высоких скоростей, тогда как при более низких скоростях пиковая нагрузка реализуется постепенно. Для скоростей, превышающих критическую, пиковая нагрузка реализуется после того, как ось колесной пары проходит эту точку, таким образом создавая несимметричное распределение нагрузки во времени.
3. Поскольку необходима математическая функция для моделирования распределения нагрузки на рельсы от колесной пары во времени с учетом докритической скорости поезда, Коррейя с соавторами (Correia et al.), от работы которых оттолкнулись Сингх и Сет [1], использовали простой подход, рассматривая решение задачи по изгибу балки на упругом основании Винклера (Winkler beam). Распределение нагрузки во времени рассчитывалось по формуле:
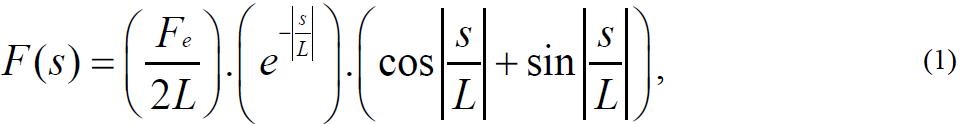
где F(s) – распределение нагрузки как функция пространственной переменной s; s – координата относительно подвижной нагрузки (движущейся системы отсчета); Fe – усилие, соответствующее нагрузке на рельсы от колесной пары; L – определяющий линейный размер (характеристическая длина);
Коррейя с соавторами (Correia et al.), на которых ссылаются авторы рассматриваемого доклада [1], рассмотрели возможный подход (принятый, например, в японских правилах), допускающий распределение нагрузки, скорректированное с учетом расстояния между шпалами (в российской практике используется собственный подход к решению этого вопроса. – Ред.). В соответствии с ним изменяемая часть нагрузки (от 40 до 60%) распределяется по соседним шпалам, а значение координаты относительно подвижной нагрузки (движущейся системы отсчета) рассчитывается с использованием следующего уравнения:

где x – глобальная координата положения поезда; vo – скорость поезда; t – время.
При s = 0 получается: 60% нагрузки на рельсы от колесной пары и L = 0,831.
Распределение единичной нагрузки, соответствующее оси каждой колесной пары, представлено на рисунке 1.
![Рис. 1. Распределение единичной нагрузки, соответствующее оси каждой колесной пары [1]. По оси абсцисс – время (c), по оси ординат – усилие (ед. изм. авторы доклада [1] не указали)](/images/dynamic/img44077.jpg)
Суммарный эффект от всех колесных пар получается с использованием принципа наложения (суперпозиции):

где Fnet – результирующее усилие от нагрузок от всех колесных пар; Fi – усилие от нагрузки от i-той колесной пары.
Авторы доклада [1] подчеркивают, опять же ссылаясь на работу Коррейя с соавторами (Correia et al.), что моделирование должно быть начато за некоторое время до того, как поезд прибудет в первое сечение расчета, поскольку его воздействие начинается до того, как он достигнет этого сечения. Соответственно, вычисление должно завершиться через некоторое время после того, как ось последней колесной пары пройдет последнее сечение расчета. Этот дополнительный промежуток времени рассчитывается путем деления расстояния, до которого рассматривается влияние нагрузки от оси колесной пары, на скорость поезда. Это расстояние называется запасным (дополнительным).
Нагрузка от каждой колесной пары здесь считается одинаковой. Разница в пиковом значении возникает из-за размещения нагрузок от колесных пар друг относительно друга. Если их оси расположены близко друг к другу, то при наложениях нескольких нагрузок получаются более высокие пики.
Моделирование и расчеты в PLAXIS 3D
Для моделирования в программном комплексе PLAXIS 3D авторы доклада [1] рассматривали массив грунта размером 40 м x 40 м x 25 м с использованием стандартных неподвижных и поглощающих границ для уменьшения отражений волн от них.
Был смоделирован типичный рельсовый путь с рельсами, системой рельсовых скреплений и шпалами, опирающимися на балласт и подстилающие слои грунта.
С помощью команды «Создать тоннель» (Create Tunnel) Сингх и Сет [1] «выстроили» на глубине 20 м от дневной поверхности двойную систему тоннелей (каждый – с круглым поперечным сечением радиусом 2,85 м). При этом была принята бетонная обделка толщиной 0,25 м с использованием линейно-упругой (Linear Elastic) модели материала.
Рельс моделировался как элемент балки длиной 50 м с прямоугольным поперечным сечением, по своим свойствам напоминающий стандартный рельс UIC 60. Каждая шпала соединялась с рельсом двумя рельсовыми скреплениями (здесь стоит отметить интересный подход авторов статьи [1] к моделированию рельсовых скреплений: для учета взаимодействия рельсов и шпал они использовали межузловые анкеры (node-to-node anchors), которым можно задать осевую жесткость. – Ред.). Стандартная шпала B70 моделировалась как балочный элемент с требуемыми моментом инерции и площадью поперечного сечения. Всего было предусмотрено 67 шпал с межцентровыми расстояниями 60 см.
В программу были введены следующие показатели свойств рельса: площадь поперечного сечения 7,7*10-3; удельный вес 78 кН/м3; модуль Юнга 200*106; момент инерции относительно второй оси 3,055*10-5 м4; момент инерции относительно третьей оси 5,13*10-6 м4.
Для шпалы были введены: площадь поперечного сечения 5,13*10-2; удельный вес 25 кН/м3; модуль Юнга 36*106; момент инерции относительно второй оси 0,0253 м4; момент инерции относительно третьей оси 2,45*10-4 м4.
На рисунке 2 показана модель двойной системы тоннелей в массиве грунта, полученная в PLAXIS 3D.
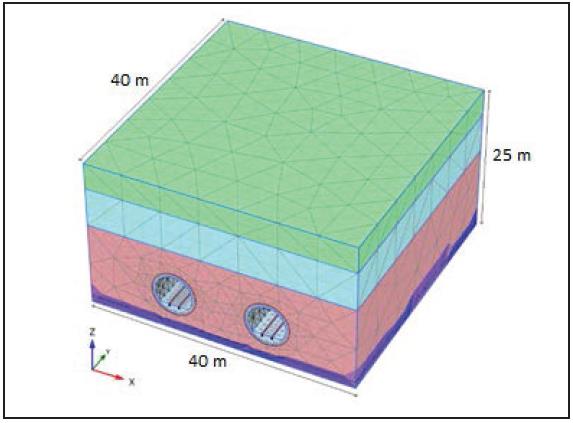
Каждое рельсовое скрепление, заданное при моделировании как элемент «межузловой анкер» (node-to-node anchor), характеризовалось следующими тремя основными параметрами: максимальная сила растяжения 312 кН; максимальная сила сжатия 1716 кН; осевая жесткость 2*106 кН.
При работе в PLAXIS 3D индийские исследователи [1] использовали три вида конститутивных (определяющих) моделей: линейно-упругую (Linear Elastic), Мора – Кулона (Mohr-Coulomb) и упрочняющегося грунта при малых деформациях (Hardening Soil Small) (авторы доклада [1], видимо, ошибочно пишут для слоя песка то просто о модели упрочняющегося грунта, то о модели упрочняющегося грунта при малых деформациях, но, судя по всему, во всех случаях имеется в виду второе. – Ред.).
Самый верхний слой, сложенный песком, моделировался с помощью модели упрочняющегося грунта при малых деформациях. Средний слой, сложенный песчаной глиной (суглинком), – с использованием линейно-упругой модели. А самый нижний слой, сложенный глиной, – с помощью модели Мора – Кулона. (Сложно предположить, чем вызван такой выбор. В статье [1] не приводится описание исходных данных по грунтам и обоснование выбора моделей грунта. По всей видимости, все зависело от имевшихся данных испытаний. Следует отметить, что для таких задач действительно предпочтительнее использовать модель упрочняющегося грунта при малых деформациях (Hardening Soil Small), которая «умеет» повышать жесткость при малых деформациях. – Ред.)
Свойства различных слоев грунта, которые были использованы индийскими исследователями [1] при моделировании, приведены в таблице.
Таблица. Свойства слоев грунта, использованные авторами доклада [1] при моделировании

Для моделирования поведения слоя на основе линейно-упругой модели использовались величины стандартной плотности грунта в водонасыщенном и неводонасыщенном состоянии, а также коэффициент Пуассона и модуль сдвига.
Для моделирования на основе модели упрочняющегося грунта при малых деформациях по секущему модулю были рассчитаны одометрические параметры, касательные параметры, модуль сдвига при разгрузке и повторном нагружении, эталонный модуль сдвига и деформация сдвига, а также некоторые другие основные и расширенные параметры.
Расчеты выполнялись в три этапа.
1. Выполнялся стандартный расчет природных напряжений (генерация исходных напряжений) при активном уровне грунтовых вод.
2. Использовался тип расчетов для неупругой деформации в дренированных условиях. На этом этапе должны были быть активизированными все элементы рельсового пути (шпалы, рельсы и рельсовые скрепления).
3. Проводился динамический расчет для учета вибрационного воздействия. На этом этапе все динамические точечные нагрузки на рельс были активны.
Во время моделирования с помощью указанных выше конститутивных моделей для разных слоев грунта скорость волн изменялась в определенном диапазоне.
Для динамических условий вместо смещений Сингх и Сет [1] использовали скорости, чтобы избежать двойного интегрирования и предотвратить увеличение ошибок в низкочастотной области.
Авторы доклада [1] напоминают, что амплитуда скорости уменьшается при распространении волны в более глубокие слои грунта, основными причинами чего является демпфирование вследствие внутреннего трения в материале и геометрическое затухание (вследствие геометрического расхождения). Но в своей модели индийские исследователи [1] учитывали только геометрическое затухание.
В пакете прикладных программ MATLAB с использованием языка программирования C++ авторы работы [1] разработали программу для формирования матрицы динамических коэффициентов (dynamic multiplier matrix) для каждой статической точечной нагрузки, приложенной вдоль рельсового пути на каждом временном шаге. Эта матрица была нужна для задания динамической нагрузки в PLAXIS.
На рисунке 3 показан график, полученный для динамических коэффициентов по длине трассы при проходе поезда со скоростью 90 км/ч. Сингх и Сет [1] выразили удовлетворение тем, что он соответствует графику изменений нагрузки, полученному ранее Коррейя с соавторами (Correia et al.), что подтверждает правильность результатов моделирования с помощью C++.
![Рис. 3. Нагрузка от поезда, движущегося со скоростью 90 км/ч [1]. По оси абсцисс – время (c), по оси ординат – нагрузка, кН](/images/dynamic/img44080.jpg)
ВОЗМОЖНЫЕ ПУТИ ИСПОЛЬЗОВАНИЯ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Сингх и Сет [1] указывают, что полученные ими результаты могут быть использованы для качественной оценки изменений вертикальной составляющей и пиковой скорости колебаний частиц грунта (пиковой виброскорости частиц грунта – PGV) для проверки математических упрощений и последующих допущений, а также для калибровки рассматриваемого профиля грунта до глубины, где требуется прогноз этих факторов.
После калибровки предлагаемую модель в PLAXIS 3D можно использовать для прогнозирования осадок, PGV и других важных параметров, которые необходимо учитывать, при моделировании условий на рассматриваемом участке.
На рисунке 4 показаны полученные авторами доклада [1] изменения вертикальной составляющей виброскорости частиц грунта в зависимости от высоты над сводом тоннеля, а на рисунке 5 – изменения вертикальной составляющей виброскорости на поверхности земли во времени в зависимости от расстояния от свода тоннеля до дневной поверхности. Эти графики можно использовать для анализа воздействия вибраций поверхности земли, вызванных движением поездов метро, на инженерные объекты и для прогнозирования вероятных повреждений этих объектов, вызванных работой метрополитена.
![Рис. 4. Изменения вертикальной составляющей виброскорости частиц грунта в зависимости от высоты над сводом тоннеля [1]. По оси абсцисс – вертикальная составляющая виброскорости (мм/c), по оси ординат – высота над сводом тоннеля (м)](/images/dynamic/img44081.jpg)
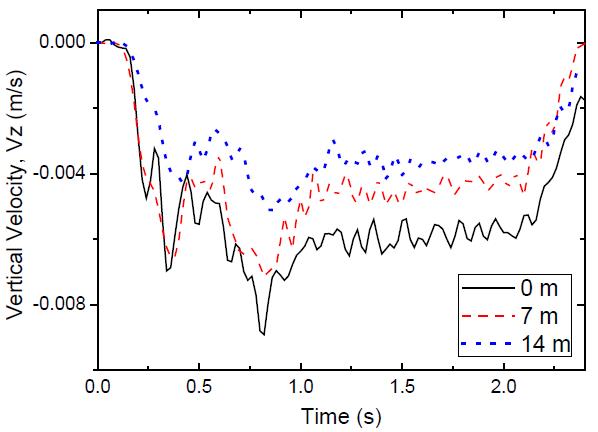
Рис. 5. Изменения вертикальной составляющей виброскорости на поверхности земли во времени в зависимости от расстояния от свода тоннеля до дневной поверхности (0; 7; 14 м) [1]. По оси абсцисс – время (c), по оси ординат – вертикальная составляющая виброскорости Vz (м/c)
ЗАКЛЮЧЕНИЕ
Таким образом, авторы доклада [1] оттолкнулись от подхода с двумерным математическим моделированием, представленного Коррейя с соавторами (Correia et al.), и расширили его до трехмерного, чтобы сформировать матрицу динамических коэффициентов (dynamic multiplier matrix). Такая матрица импортируется в PLAXIS для точного моделирования условий с подвижными нагрузками, создаваемых движущимися поездами метро. Различные параметры можно получить непосредственно путем расчетов в PLAXIS.
По итогам своей работы [1] Сингх и Сет сделали вывод об эффективности выполнения ими 3D-моделирования на основе метода конечных элементов для решения поставленных задач.
Источники
1. Singh D.V., Seth Y. 3D modelling of ground surface vibration induced by underground train movement // Procedia Engineering (by Proceedings of Implast 2016 : 11th International Symposium on Plasticity and Impact Mechanics). Elsevier, 2017. Vol. 173. P. 1580–1586. URL: sciencedirect.com/science/article/pii/S1877705816346598.
Список литературы, использованной авторами доклада [1]
A.G. Correia, J. Cunha, J. Marcelino, L. Caldeira, J. Varandas, Z. Dimitrovovб, A. Antгo, and M. G. d. Silva, “Dynamic analysis of rail track for high speed trains. 2D approach,” in 5th Intl Worksop on Application of Computational Mechanics on Geotechnical Engineering, Portugal 2007, p. 14.
M. Shahraki, M.R.S. Sadaghiani, K.J. Witt, T. Meier, 3D Modelling of Train Induced Moving Loads on an Embankment, Plaxis Bulletin Issue 36, Autumn 2014.
J.A. Lord, Railway foundations: Discussion paper, Proc. 12th ECSMGE, Geotechnical Engineering for Transportation Infrastructure (Barends et al., eds.), Balkema, Rotterdam, 1999.
T. Dahlberg, Railway track settlements - a literature review, Linkцping, Sweden, 2004.
C. Madshus and A.M. Kaynia, High-Speed Railway Lines on Soft Ground: Dynamic Behaviour at Critical Train Speed, Journal of Sound and Vibration, vol. 231, p. 689–701, 2000.
T.G. Gutowski, C.L. Dym, Propagation of ground vibration: A review, Journal of Sound and Vibration 49 (2), (1976) 179–193.
Plaxis bv, PLAXIS 3D 2011-Material-Models, vol. 3. Netherlands: PLAXIS, 2011.
Plaxis bv, PLAXIS 3D 2011-Reference, vol. 2. Netherlands: PLAXIS, 2011.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц


















