Опорное давление в программе PLAXIS». Часть 2. Выбор величины опорного давления
 Федоренко Евгений Владимировичнаучный консультант компании НИП-Информатика, к.г.-м.н., г. Санкт-Петербургeugeniy.fedorenko@nipinfor.ru
Федоренко Евгений Владимировичнаучный консультант компании НИП-Информатика, к.г.-м.н., г. Санкт-Петербургeugeniy.fedorenko@nipinfor.ru
Во второй части статьи рассмотрено, как назначать опорное давление, и почему оно всегда может быть равным атмосферному (100 кПа). Также приведены приемы обработки исходных данных перед геотехническим расчетом. Показано, что для грунта на небольшой глубине с бытовым давлением менее 100 кПа опорное давление может быть задано равным 100 кПа.
Напомним, что в статье рассматриваются исключительно математические принципы работы модели грунта hs. Правомерность использования этих принципов на практике должна быть определена на основе правильно проведенных испытаний грунтов квалифицированным специалистом инженером-геологом.

Рассмотрим более подробно, каким образом следует назначать опорное давление.
Учитывая, что опорное давление Pref принимается одинаковым, необходимо следить за выбором данных лабораторных испытаний при определении параметров для модели.
Допускается изменять значение по умолчанию Pref=100 кПа в том случае, когда трехосные испытания при этом давлении не выполнялись и принимать в этом случае в качестве опорного имеющееся в трехосных испытаниях давление σ3. Приоритетность выбора Pref на основе трехосных испытаний связана с тем, что компрессионная кривая позволяет выбрать в качестве опорного давления любое.

Однако в зарубежной практике, из которой к нам пришла эта теория, принято негласное соглашение не изменять опорное давление для того, чтобы можно было сопоставлять различные испытания одинаковых грунтов и, в конечном счете, по мере накопления данных, иметь корреляционные зависимости для быстрого принятия предварительных решений.
Удобство такого подхода можно продемонстрировать на примере оценки результатов испытаний. На рисунке 10 приведена таблица параметров модели HS для четвертичных отложений, имеющих различающиеся значения опорного давления. Сложно при разном опорном давлении понять, почему одометрический модуль деформации суглинка мягкопластичного может быть больше, чем у суглинка тугопластичного. При одинаковом значении опорного давления (как предлагается при 100 кПа) сопоставлять значения модулей деформации проще.
![Рис. 10. Пример параметров модели HS [Мирный А.Ю. и др. «Статистический анализ параметров модели Hardening soil для грунтов московского региона» / Геотехника №4 2017]](/images/dynamic/img43482.png)
Это может быть полезным при работе с моделью Soft Soil или Soft Soil Creep, когда по заданным параметрам λ* и к* после построения компрессионной кривой в SoilTest можно легко определить одометрический модуль деформации при Pref=100 кПа, и таким образом оценить сжимаемость грунта в более привычной системе измерений, а также сопоставить его с другими данными или моделями.
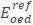
Таким образом, наиболее предпочтительным вариантом является вычисление опорного значения сдвиговой
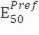
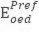
Разберемся, как это сделать.
Прежде всего, следует отметить, что величина Pref=100 кПа, а точнее 101 кПа, это ни что иное, как нормальное атмосферное давление (1 атмосфера или 1 кг/см2, как единица давления). И значение это в модели не случайно, оно основано на теории Янбу, которая вместе с теорией гиперболической зависимости между напряжениями и деформацией Дункана (1980) позволяет описывать изменение жесткости для условий трехосного сжатия. Зависимость начального модуля Еi от всестороннего обжатия определяется зависимостью (рис. 12):

где К – опорный модуль, принятый в классификации в зависимости от вида грунта и содержания глинистой фракции (табличное значение с запасом, обычно используются региональные значения);
n – так называемый «экспоненциальный модуль» гиперболической зависимости;
Ра – атмосферное давление, принимаемое равным 100 кПа.
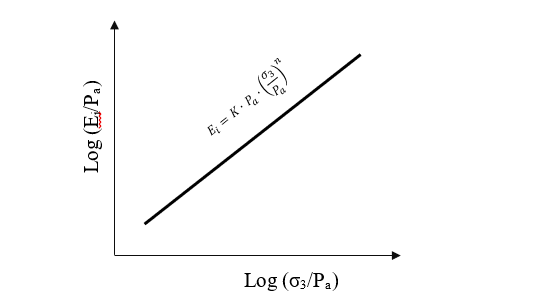
График на рисунке 12 (нормализованный по атмосферному давлению Ра) показывает, что с увеличением давления обжатия σ3 в трехосных испытаниях возрастает трехосный модуль деформации Еi (определяемый по начальному, линейному участку графика).
При разработке модели HS в качестве используемого трехосного модуля, вместо начального Еi был выбран секущий модуль Е50 при 50% значении девиатора, что позволяет модели определять пластические деформации.
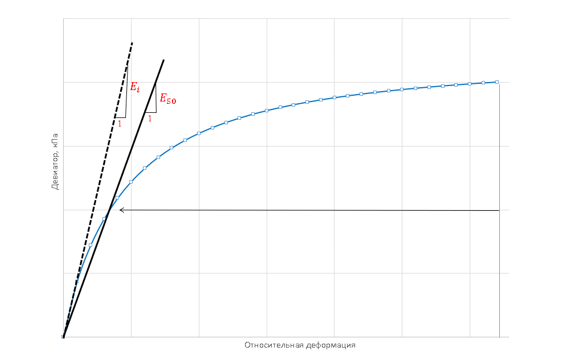
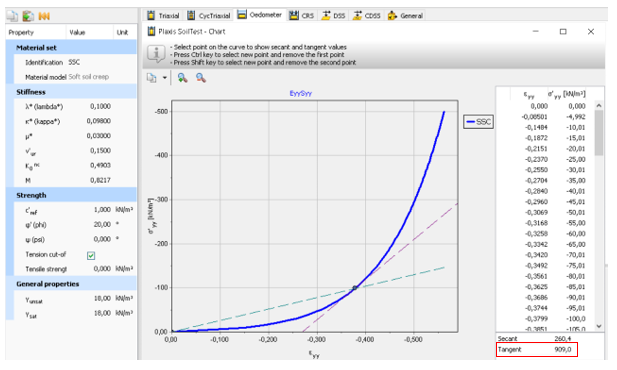
Для того, чтобы определить опорную жесткость путем пересчета, можно воспользоваться математическими свойствами зависимостей (1) и (2) (см. часть 1). Для примера на рисунке 14 приведен график зависимости одометрического модуля от нормального давления (рассматриваются компрессионные испытания).
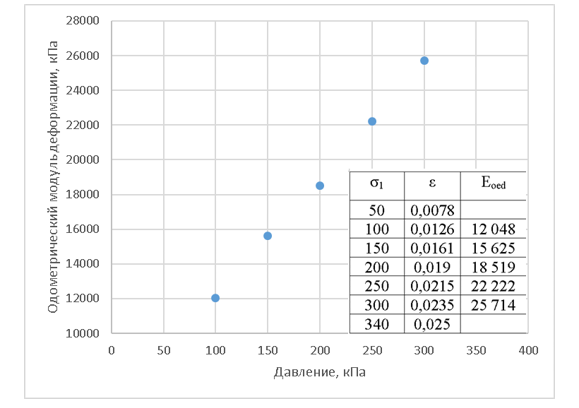
Как следует из графика, модуль деформации не является постоянной величиной, а изменяется в зависимости от уровня действующих напряжений. Для того, чтобы учесть этот факт в расчетах, современные модели грунтов используют принцип опорного давления и степенной зависимости. Использование принципа может быть проиллюстрировано следующим образом: при нормализации значений графика по опорному давлению угол наклона линии в логарифмической шкале графика определяется показателем степени m (рис. 15).
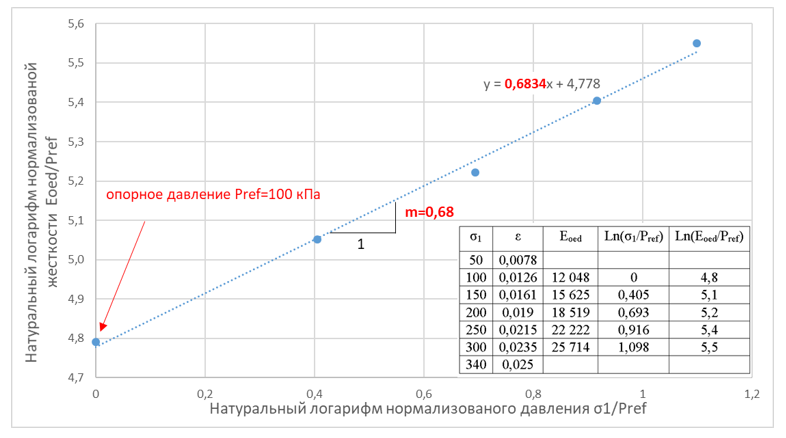
Линия тренда в MS Excel с выводом уравнения на диаграмме позволяет получить параметр m как коэффициент k в уравнении линии вида «y=k·x+b». Этот вариант определения параметра m достаточно трудоемкий, но наглядный, в практике коэффициент прямой k=m в MS Excel может быть получен без построения графиков, а лишь путем использования соответствующей функции, имеющий синтаксис: «=НАКЛОН (значения y, значения x)».
Для линии на рисунке 15 вычисленное значение модуля деформации при давлении 300 кПа составит:
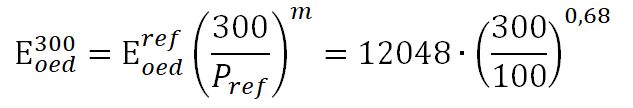
Небольшие расхождения связаны с осреднением точек прямой линией (опорное давление по линии немного меньше, чем в точке).
Пример 3. Грунт залегающий на малой глубине
Учитывая, что грунты имею сцепление, использование указанного приема для получения параметра m связных грунтов неприемлемо. Для них используется аналогичный подход, но основанный уже на зависимостях (1) и (2). Для примера рассмотрим интерпретацию трехосных испытаний. Три консолидированно-дренированных опыта были проведены на трех образцах-близнецах при всестороннем обжатии: 34,5; 138; 345 кПа (испытания при давлении 100 кПа не проводились). Для каждой кривой зависимости «σ1- σ3 – ε1» получен секущий модуль деформации при 50% уровне напряжений
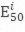
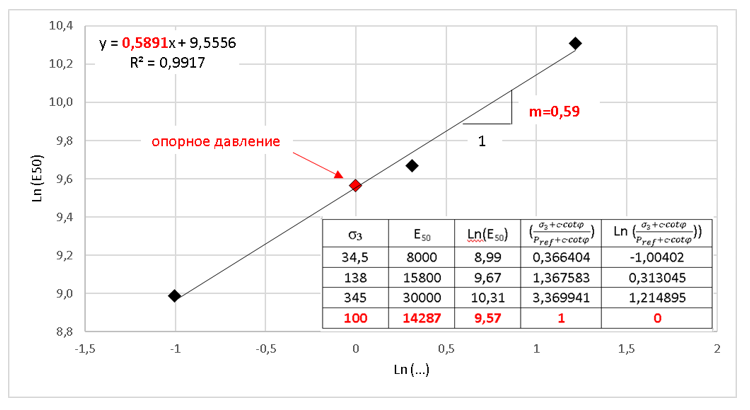
На рисунке 16 показан принцип построения графика зависимости между секущим трехосным модулем деформации Е50 и выражением, стоящим в скобках в формуле:
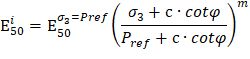
График строится в логарифмических осях по натуральному логарифму.
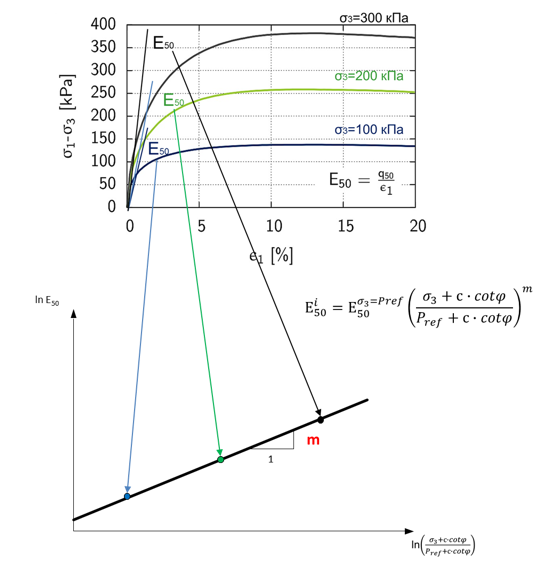
Учитывая тот факт, что график в логарифмических осях позволяет считать зависимость между натуральным логарифмом Е50 и натуральным логарифмом выражения в скобках линейной, определение параметра m таким способом имеет как минимум два преимущества:
- возможность статистической обработки результатов испытаний;
- возможность определить опорное давление для рекомендованного значения Pref=100 кПа.
Последний пункт необходим в таких случаях, как:
1) рассматриваемая в этом примере ситуация, когда трехосные испытания при давлении обжатия 100 кПа не выполнялись;
2) для переуплотненных грунтов.
Пересчет выполняется путем определения по полученной зависимости значения
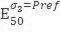
На рисунке 17 приведен график в логарифмических осях, на котором черным цветом показаны точки испытаний (давление обжатия: 34,5; 138; 345 кПа), а красным – вычисленное значение опорного модуля
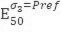
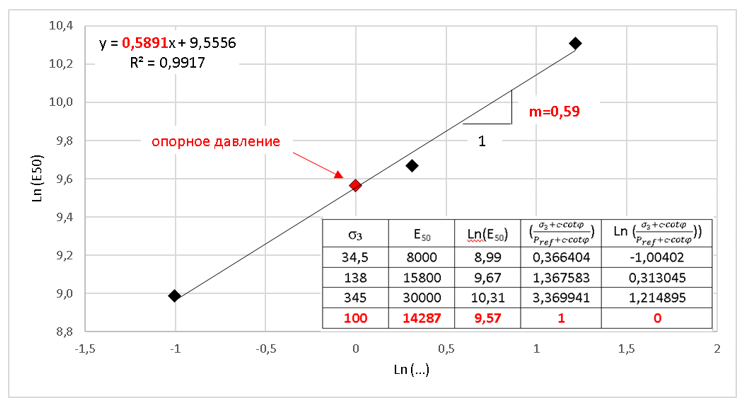
Таким образом, в этом примере несмотря на отсутствие трехосного испытания с обжатием 100 кПа, в качестве опорного давления принято Pref=100 кПа, а соответствующий опорный трехосный модуль определен путем пересчета и составил
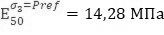
Пример 4. Сравнение поведения при разном опорном давлении
В этом примере рассмотрен условный массив грунта размером 1x1 м. прикладываются напряжения от собственного веса (initial phase + gravity loading). На рисунке 18 показана расчетная схема и результаты расчетов в виде распределения напряжений от собственного веса в схеме и на эпюре. Цифрами обозначены напряжения на кровле, середине и подошве слоя, а на эпюре показаны средние значения. Для дельнейших рассуждений слой условно разделен на два по 0,5 м.
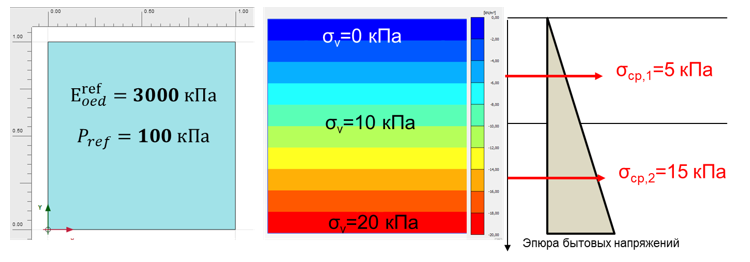
Рассмотрен вариант расчета для следующих параметров модели HS:
- Pref=100 кПа,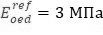
В соответствии с известными представлениями о выборе модуля деформации (линейная зависимость участка компрессионной кривой между бытовыми напряжениями и напряжениями от нагрузки) определены одометрические модули для каждого из выделенных слоев (рис. 19.), а также для всего слоя по средним напряжениям (рис. 20).
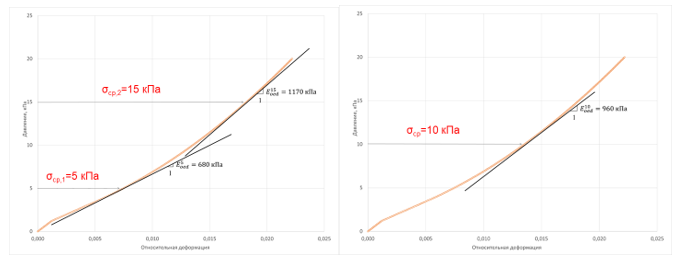
По графикам на рисунке 20 получено:
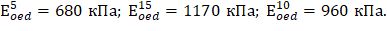
Определим деформации от собственного веса для рассматриваемого массива, разделенного на два слоя:
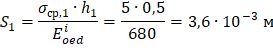
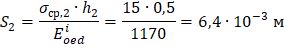
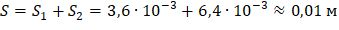
Упрощенный расчет (для условий компрессионного сжатия) показывает, что деформации составят около 1 см. Расчет в PLAXIS (более точно) показывает близкие результаты: S=1,3 см (рис. 20).
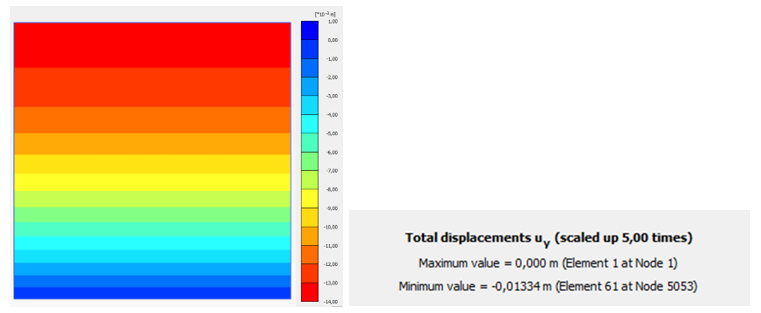
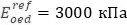
Следует напомнить, что был задан модуль деформации
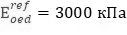
Для наглядности приводится результат расчета для варианта с опорным давлением в 10 раз меньше: Pref=10 кПа,
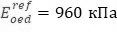
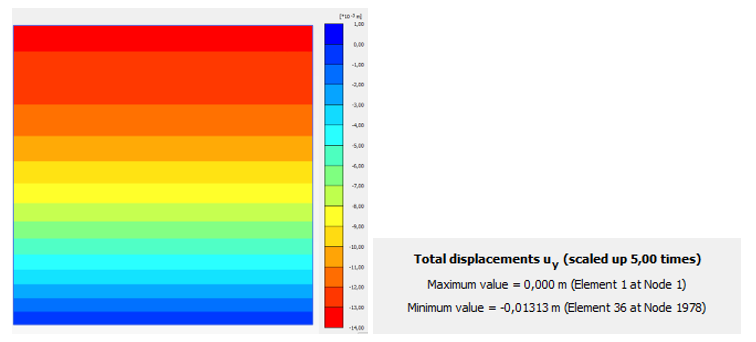
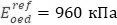
Как следует из сопоставления результатов (рис. 21 и рис. 22) результаты одинаковые. Ручной счет по упрощенной зависимости для однослойного массива подтверждает выполненные расчеты:
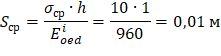
Нетрудно догадаться, что в том случае, когда модуль деформации для рассматриваемого диапазона напряжений был определен верно (например, для одного слоя
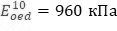
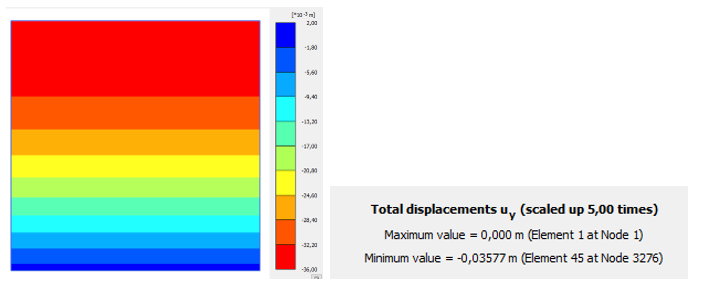
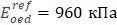
Как видно из рисунка 22, деформации увеличились в 3 раза, что связано с тем, что теперь опорным модулем для глубины около 5 м (при γ=20 кН/м3: Pref/γ г=z) является значение
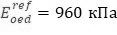

Рекомендуется, в тех случаях, когда параметры модели HS задаются по одному значению модуля деформации Е0 (для предварительных расчетов), назначать в качестве опорного давления среднее между действующим и дополнительным. Тогда ожидаемое значение модуля деформации не будет пересчитываться и пойдет в расчет.
Таким образом, модель HS позволяет прогнозировать изменение жесткости как «вперед», так и «назад» по кривой испытания. Точность прогноза зависит от качества образцов, правильности обработки результатов и возможности модели описать эти результаты.
Продолжение следует.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц