PLAXIS 2D показал преимущества мостов с «изолированными» интегральными устоями

ВВЕДЕНИЕ

Мостовые сооружения (далее – мосты) являются одними из ключевых элементов транспортной инфраструктуры и требуют больших вложений в их строительство и последующее обслуживание. Более дешево обходятся мосты с интегральными устоями. Это рамные сооружения, которые не имеют деформационных швов, шарнирных или скользящих конструкций. Сплошное тело интегрального устоя устраивается в пределах глубины подходной насыпи (рис. 1, 2). Особенно ценно то, что при правильном проектировании такие мосты практически не требуют технического обслуживания. И  это в последнее время привлекает к ним большое внимание, поскольку в отрасли ищутся надежные решения при меньших затратах.

Рис. 1. Один из вариантов однопролетного моста с интегральными устоями [1]

Рис. 2. Один из вариантов сопряжения интегрального устоя с насыпью подхода к мосту [1]

Однако взаимодействие между интегральными устоями и грунтом подходных насыпей из-за циклов температурного расширения и сжатия конструкций при сезонных и суточных колебаниях температуры, а также из-за динамических нагрузок от движения транспорта, воздействия ветра, сейсмических событий и пр. обычно позволяет использовать такие конструкции только для мостов с малыми и иногда средними пролетами – как правило, не длиннее 30 м (реже до 50–100 м и только в исключительных случаях больше).

Указанные воздействия на конструкции мостов приводят к долгосрочным последствиям: к накоплению в подходных насыпях остаточных деформаций с возникновением смещений, уплотнения и осадок насыпного грунта, а при динамических воздействиях иногда и к его разуплотнению с увеличением объема. Эти процессы ведут к нарушению сопряжения интегрального устоя с насыпью, к чрезмерным нагрузкам на него, его деформациям и смещениям. В итоге при въезде на мост возникают неровности и трещины в дорожном покрытии, что требует проведения существенных ремонтных работ и соответствующих периодических затрат. Особенно сильно такие последствия проявляются при увеличении длины пролетов, что обычно не дает возможности использовать интегральные устои для большепролетных мостов [1–5].

Поэтому в последние годы появляется много отечественных и зарубежных публикаций по улучшению сопряжения интегральных устоев с подходными насыпями, а также по увеличению длины пролетов интегральных мостов. Предлагаются самые разные способы. Здесь мы разберем материалы доклада «Численное исследование сейсмического отклика инновационных проектов мостов с интегральными устоями и сравнение его результатов с существующей практикой проектирования» [5], который сделали исследователи из Великобритании и Германии А. Каристо, А. Палеохорино и С. Митулис на 1-й Международной конференции по опасным природным явлениям и инфраструктуре (ICONHIC 2016), проходившей в греческом городе Ханья на острове Крит в 2016 году.

Авторы указанного доклада провели нелинейный анализ изменений во времени двух двумерных численных моделей большепролетных мостов с интегральными устоями после ряда сейсмических воздействий с использованием конечноэлементной программы PLAXIS 2D (ее версии 8.2). В первом случае рассматривались обычные интегральные устои, непосредственно контактировавшие с грунтом подходных насыпей, а во втором они были отделены от насыпного грунта сжимаемым заполнителем из измельченных отработанных шин (использовать такую «изоляцию» авторы доклада впервые предложили в более ранней публикации [8]).

ВХОДНЫЕ ДАННЫЕ ПРИ МОДЕЛИРОВАНИИ В  PLAXIS 2D

Свойства грунта подходной насыпи и грунта основания моста

В качестве грунта для формирования подходных насыпей при численном моделировании авторы доклада [5] рассматривали уплотненный песок с углом внутреннего трения 42 град. и углом дилатансии 10,9 град. В качестве основания они выбрали толщу грунта типа B по Еврокоду 8-1 (очень плотный песок, гравий или твердую глину [6]).

Было принято, что поведение и насыпного грунта, и грунта основания является упругопластическим; при этом учитывался критерий Мора – Кулона. Нелинейность поведения грунта для диапазона деформаций от низких до средних, модули и параметры демпфирования грунта были оценены на основе одномерного эквивалентного линейного анализа. Жесткость и демпфирование были основаны на калибровке, выполненной на уровне деформаций согласно Еврокоду 8 (CEN EN 1998-1). Для более сильных деформаций влияние нелинейности учитывалось с помощью критерия прочности Мора – Кулона.

Свойства грунта насыпи и грунта основания приведены в таблице 1.

Таблица 1. Свойства грунта насыпи и грунта основания моста с интегральными устоями [5]

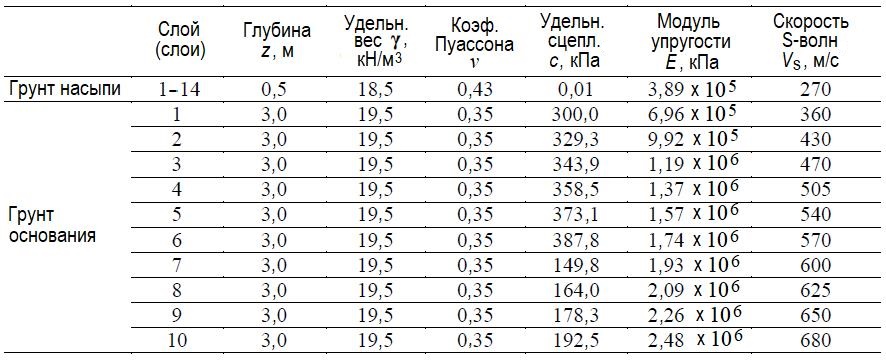
Свойства сжимаемого заполнителя

Свойства сжимаемого заполнителя («изолятора») из измельченных отработанных шин для второй модели были определены при лабораторных испытаниях, проведенных в Университете Суррея (Великобритания) и в Университете Аристотеля (г. Салоники, Греция). На основании результатов, полученных в своих предыдущих исследованиях, авторы доклада [5] приняли при численном моделировании следующие параметры для этого материала: коэффициент Пуассона 0,49; модуль упругости 56,9 кПа; удельный вес 6,1 кН/м³. При этом толщина вертикальной прослойки из сжимаемого заполнителя между интегральным устоем и грунтом подходной насыпи была принята равной 300 мм.

Динамические нагрузки

Сейсмические воздействия на численные модели мостов, использованные авторами работы [5] в качестве циклических динамических нагрузок, представляли собой семь записей колебаний грунта при реальных землетрясениях (табл. 2). Эти записи были нормированы на среднюю величину пикового ускорения грунта (PGA), типичную для европейских сейсмически опасных районов, то есть на 0,3g. Все они соответствовали упругому спектру по Еврокоду 8-1 для грунта типа B. Их выбор был обоснован возможностью учета среднего распределения результатов в соответствии с Еврокодом 8-2.

Таблица 2. Сейсмические сигналы, использованные при моделировании [5]

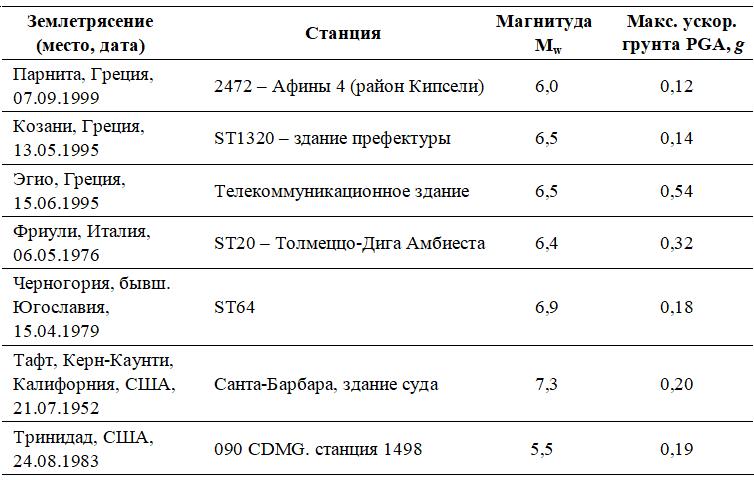
Для определения реакций системы «устой – насыпь» как на сейсмические колебания, индуцированные в фундаменте устоя, так и на сейсмический отклик пролетного строения моста был использован подход «декаплинг» (искусственное ослабление сейсмического сигнала).

Демпфирующие свойства системы основывались на результатах, полученных при другом исследовании [7].

Приведенные в таблице 2 сейсмические воздействия использовались в качестве входных временных зависимостей для основания модели, чтобы получить продольный динамический отклик системы.

ДВУМЕРНОЕ МОДЕЛИРОВАНИЕ В PLAXIS 2D

Анализ комплексного взаимодействия между грунтом и сооружением для мостов с интегральными устоями при сейсмических нагрузках авторы доклада [5] выполняли с помощью версии 8.2 конечноэлементной программы PLAXIS 2D для плоской деформации.

Как уже упоминалось, были разработаны две 2D модели моста. Первая – с обычным интегральным устоем (со свайным фундаментом), непосредственно контактирующим с грунтом насыпи. Вторая – с вертикальной прослойкой из сжимаемого заполнителя из измельченных шин между устоем и грунтом насыпи, стабилизированным механическим путем (уплотнением и армированием георешетками с осевой жесткостью EA = 10⁵ кН).

Модели имели общую длину 282 м и общую высоту 36 м и были выполнены с использованием 15-узловых треугольных элементов (в общей сложности 47 317 узлов).

Предварительный анализ чувствительности моделей показал, что их принятая длина достаточна для минимизации краевых эффектов без значительного увеличения вычислительных затрат. При этом для моделирования поведения среды в дальней зоне и во избежание краевых эффектов использовались поглощающие границы при динамических нагрузках.

Предварительно напряженная железобетонная плита пролетного строения моста была смоделирована с использованием пластинчатого элемента, к которому непосредственно применялись осевая и изгибная жесткость. Общая осевая жесткость моста EA была принята равной 2,222*10⁷ кН, при этом изгибная жесткость EI составила 4,56*10⁶ кН*м².

В модели моста с обычными интегральными устоями (модели № 1) использовалось 14 слоев насыпного грунта, контактирующего с устоями. Для лучшего моделирования контакта между этими двумя разными видами материалов использовались интерфейсные элементы между слоями насыпи и железобетонными устоями.

В модели моста с интегральными устоями, отделенными от насыпного грунта сжимаемым заполнителем из измельченных шин (модели № 2), использовались: вертикальная прослойка сжимаемого заполнителя между грунтом насыпи и устоями; 14 слоев насыпного грунта; элементы георешеток, стабилизирующих насыпь (георешетки были применены как горизонтально, так и вертикально).

Был определен и кластер для моделирования пустоты (воздуха) под пролетным строением моста (рис. 3).

Рис. 3. Двумерная модель рассматриваемого моста с интегральными устоями, отделенными от грунта подходной насыпи сжимаемым заполнителем из измельченных шин (модель № 2, полученная в программе PLAXIS 2D) (по [5])

В своем исследовании [5] авторы упростили ситуацию и не учитывали при моделировании температурные деформации, ползучесть и усадку, которые происходили до сейсмических воздействий. Для обеих моделей были учтены только начальные геостатические напряжения, а также напряжения, возникающие на этапах строительства для устоев, сжимаемого искусственного заполнителя и грунта насыпей, чтобы учесть влияние, которое оказывает на долговременное поведение системы последовательность приложения нагрузок.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Давление грунта на интегральный устой

Высокие давления на устои после сейсмического воздействия (даже если они являются конструктивно приемлемыми сразу после толчка) в сочетании с циклами температурного расширения/сжатия сооружения могут постепенно привести к ухудшению сопряжения устоев с подходными насыпями и повреждениям моста. Следовательно, очень важно контролировать и уменьшать давление на устои.

Для обычной системы (модели № 1) максимальное давление насыпного грунта на вертикальную поверхность устоя после сейсмического события составило 269,1 кН/м² после сейсмических колебаний, характерных для землетрясения в Черногории (см. табл. 2).

Для системы с сжимаемым заполнителем из измельченных шин между устоем и грунтом насыпи (модели № 2) максимальное давление на стенку устоя после того же события составило 14,9 кН/м², то есть примерно в 18 раз меньше, чем для первой модели. Примерно то же самое характерно и для остальных сейсмических воздействий (см. табл. 2).

Кроме того, распределение давлений на вертикальную поверхность устоя является нелинейным с максимальным значением примерно на середине высоты для модели № 1 и почти линейным с максимальным значением на уровне подошвы устоя для модели № 2 (рис. 4). Линейное распределение давлений для второй модели было признаком того, что насыпь не нарушается из-за смещений устоя (кроме того, для «изолированного» устоя в этом случае точка приложения силы сместилась вниз, что привело к общему уменьшению опрокидывающего момента, действующего на устой моста, а это, например, дает возможность снизить материалоемкость).

Рис. 4. Давление грунта на левый (а) и правый (б) интегральные устои моста после сейсмического воздействия?(по [5]). Сплошная жирная линия?– средние значения по семи воздействиям для системы с обычным интегральным устоем (№ 1); пунктирная жирная линия – средние значения по семи воздействиям для системы с «изолированным» интегральным устоем (№ 2); тонкие сплошные линии?– средние квадратичные отклонения 

Интересно отметить, что величины давления грунта на обычный интегральный устой (в модели № 1) показали значительный разброс для семи разных воздействий. Однако распределения давлений и их пиковые значения для системы с «изолированными» устоями (модели № 2) получились практически одинаковыми после всех воздействий (см. рис. 4), то есть произошло почти полное отделение системы «сжимаемый заполнитель – устой» от грунта насыпи, причем это подтвердила идентификация периодов сейсмических откликов (но ее результаты авторы доклада [5] не представили).

Следует также отметить несимметричное поведение левого и правого устоев для модели № 1, что напрямую связано с несимметричностью воздействия от сейсмического события. Однако для модели № 2 поведение левого и правого устоев почти симметрично, так как их отклик не связан с ответом грунта насыпей, отделенного от устоев сжимаемым заполнителем (см. рис. 4).

Долговременные вертикальные смещения грунта подходных насыпей

Одной из задач правильного проектирования мостов с интегральными устоями является контроль вертикальных деформаций грунта подходных насыпей, чтобы избежать трещин и неровностей дорожного покрытия при въезде на мост и минимизировать затраты на его техническое обслуживание.

На основе результатов моделирования авторы работы [5] выявили, что все сейсмические воздействия привели к разуплотнению насыпного грунта с формированием выпора вблизи обычных интегральных устоев на величины до 90 мм. Вблизи же «изолированных» устоев подъем поверхности произошел только в двух случаях и не более чем на 8 мм, а в остальных случаях возникли небольшие просадки – не более чем на 9 мм (табл. 3).

Таблица 3. Максимальные вертикальные смещения грунта насыпи после сейсмических воздействий [5]

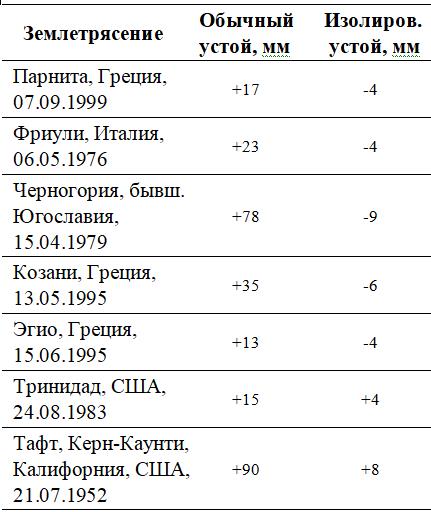
На рисунке 5 показаны изменения средних долговременных вертикальных смещений насыпного грунта после сейсмического воздействия в зависимости от расстояния от устоя и их средних квадратичных отклонений. Следует отметить, что величины вертикальных деформаций на поверхности насыпей для обычных систем (модели № 1) показали значительный разброс для семи разных воздействий, а для «изолированных» систем (модели № 2) разброс был гораздо меньше.

Рис. 5. Вертикальные смещения поверхности насыпи в зависимости от расстояния от левого (а) и правого (б) интегральных устоев моста (по [5]). Сплошная жирная линия – средние значения по семи воздействиям для системы с обычным интегральным устоем (№ 1); пунктирная жирная линия – средние значения по семи воздействиям для системы с «изолированным» интегральным устоем (№ 2); тонкие сплошные линии – средние квадратичные отклонения

Отраженное в таблице 3 и на рисунке 5 разительное уменьшение вертикальных смещений после сейсмических событий в случае отделения интегральных устоев от насыпи сжимаемым заполнителем говорит о том, что такой мост не будет поврежден после толчков с магнитудой 5,5–7,3 (см. табл. 2).

Поведение устоев

По приведенным ранее распределениям давлений на устои авторы доклада [5] получили эпюры изгибающих моментов, индуцированных в этих конструкциях после сейсмического воздействия (рис. 6).

Рис. 6. Эпюры изгибающих моментов для левого (а) и правого (б) интегральных устоев моста после сейсмического воздействия (по [5]). Сплошная жирная линия – средние значения по семи воздействиям для системы с обычным интегральным устоем (№ 1); пунктирная жирная линия – средние значения по семи воздействиям для системы с «изолированным» интегральным устоем (№ 2); тонкие сплошные линии – средние квадратичные отклонения

Для обычного интегрального устоя (модели № 1) максимальный положительный изгибающий момент составил 173 кН*м/м, а максимальный отрицательный – 258 кН*м/м. Для «изолированного» устоя (модели № 2) максимальный положительный изгибающий момент был равен 7,04 кН*м/м, а максимальный отрицательный – 12,94 кН*м/м (то есть примерно в 25 и в 20 раз меньше, чем в первом случае). При этом среднеквадратичное отклонение для первой модели составило ±45 кН*м/м, тогда как для второй оно оказалось пренебрежимо малым.

Кстати, максимальное значение средней поперечной (сдвиговой) силы было равно 167 кН/м для обычной системы и всего 10 кН/м для «изолированной».

ВЫВОДЫ

Таким образом, путем численного моделирования в версии 8.2 программы PLAXIS 2D авторы доклада [5] показали, что отделение интегрального устоя моста от подходной насыпи прослойкой из сжимаемого заполнителя из измельченных шин с одновременным армированием материала насыпи с помощью георешеток приводит к поразительному снижению вертикальных деформаций насыпного грунта и величин его давления на устой, а также к уменьшению сил сдвига и изгибающих моментов в самом устое. Эти эффекты были получены при моделировании сейсмических воздействий и, очевидно, будут наблюдаться и при других циклических нагрузках.

Это не только повышает надежность мостовых сооружений с интегральными устоями, но и позволяет экономить как на их строительстве (за счет размеров, прочности и необходимого армирования устоев), так и на их техническом обслуживании. Кроме того, появляется возможность проектировать интегральные мосты с более длинными пролетами, в том числе в сейсмоопасных регионах.

При этом авторы работы [5] считают, что в дальнейшем необходимы детальные исследования гистерезисного поведения разъединяющего сжимаемого заполнителя, а также тщательное изучение влияния, которое такая «изоляция» интегральных устоев может оказать на подходы к проектированию, строительству, техническому обслуживанию мостовых сооружений и на соответствующие затраты.

—

Статья подготовлена при поддержке компании «НИП-Информатика» — партнера журнала «ГеоИнфо».

Источники

1. Попов В.И. Мосты с интегральными устоями. М.: АО «Институт «Стройпроект», МАДИ, URL: http://new.groteck.ru/images/catalog/116448/4bcb0b1e8bdc3cf3d68a7635a37527b7.pdf.
2. Попов В.И. Совершенствование конструкции сопряжения путепроводов с насыпью путем применения интегральных устоев // Дороги и мосты. 2014. № 31 (1). С. 166–180. https://docplayer.ru/46424846-Udk-sovershenstvovanie-konstrukcii-sopryazheniya-puteprovodov-s-nasypyu-putem-primeneniya-integralnyh-ustoev.html.
3. Попов В.И., Зунг Ч.Д. Современные способы снижения деформаций насыпей подходов к мостам // Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). 2019. № 2 (57). URL: https://elib.pstu.ru/vufind/EdsRecord/edselr,edselr.38516259.
4. Попов В.И., Прохоров А.А. Способы сопряжения конструкций путепроводов с насыпями подходов // Науковедение. 2014. № 5 (24). URL: https://naukovedenie.ru/PDF/25KO514.pdf.
5. Caristo A., Palaiochorinou A., Mitoulis S. Numerical research on the seismic response of novel integral abutment bridge designs and comparison to the current design practice // Proceedings of the 1-st International Conference on Natural Hazards and Infrastructure, 28–30 June, 2016, Chania, Greece. URL: https://kipdf.com/numerical-research-on-the-seismic-response-of-novel-integral-abutment-bridge-des_5b1441ac7f8b9a2f448b4594.html.
6. https://eurocodes.jrc.ec.europa.eu/doc/WS_335/S2_EC8-Lisbon_E%20CARVALHO.pdf.
7. Mitoulis S., Argyroudis S., Kowalsky M. Evaluation of the stiffness and damping of abutments to extend direct displacement based design to the design of integral bridges // Proceedings of the 5-th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015), Crete Island, Greece, 25–27 May 2015. URL: https://www.researchgate.net/conference-event/COMPDYN_International-Conference-on-Computational-Methods-in-Structural-Dynamics-and-Earthquake-Engineering_2015/3138.
8. Mitoulis S., Palaiochorinou A., Georgiadis I., Argyroudis S. Extending the application of integral frame abutment bridges in earthquake prone areas by using novel isolators of recycled materials // Earthquake Engineering and Structural Dynamics. 2016. V. 45 (14). P. 2283–2301. URL: https://epubs.surrey.ac.uk/810563/.

Список литературы, использованной авторами доклада [5]

1. ASCE. Report card for America’s infrastructure, 2013.
2. Mistry V.C., Al Mangus. Get in, stay in, get out, stay out. United States: Federal Highway Administration, Department of Transportation, 2006. Vol. 70. № 3. FHWA-HRT-2006-001.
3. INTAB. Economic and durable design of composite bridges with integral abutments. Research Program RFSC RFS-P2-08065, European Commission, Brussels, 2010.
4. IABSE. Special issue on integral bridges // Structural Engineering International. 2011. Vol. 2.
5. Dicleli M., Eng P., Albhaisi S.M. Maximum length of integral bridges supported on steel H-piles driven in sand // Engineering Structures. 2003. Vol. 25. P. 1491–1504.
6. Mitoulis S.A., Tegos I.A. Two new earthquake resistant integral abutments for medium to long-span bridges // Structural Engineering International. International Association for Bridge and Structural Engineering (IABSE), 2011. Vol. 21. № 2. P. 157–161.
7. Baptiste K.T., Kim W., Laman J.A. Parametric study and length limitations for prestressed concrete girder integral abutment bridges // Structural Engineering International. 2011. Vol. 21. № 2. P. 151–156.
8. Mitoulis S.A., Tegos I.A., Stylianidis K.-C. Cost-effectiveness related to the earthquake resisting system of multi-span bridges // Engineering Structures. 2010. Vol. 32. № 9. P. 2658–2671.
9. Kappos A.J., Sextos A.G. Seismic assessment of bridges accounting for nonlinear material and soil response and varying boundary conditions // NATO Science for Peace and Security. Series C: Environmental Security. 2009. Vol. 3. P. 195–208.
10. Mitoulis S.A. Seismic design of bridges with the participation of seat-type abutments // Engineering Structures. 2012. Vol. 44. P. 222–233.
11. England G.L. A thermal displacement compensation unit for integral bridges // Patents. Bridge structures. 2005. P.N.: CA 2605437 A1.
12. Horvath J. Lateral pressure reduction on earth-retaining structures using geofoams: correcting some misunderstandings // Proceedings of the 3-d ASCE Earth Retention Conference. 2010. P. 862–869.
13. Hoppe E.J. Field study of integral backwall with elastic inclusion: final report. Charlottesville: Virginia Transportation Research Council, 2005.
14. Potzl M., Naumann F. Fugenlose betonbruken mit flexiblen widerlagern // Beton- und Stahlbetonbau. 2005. Band 100. № 8.
15. Arsoy S., Duncan J., Barker R. Behavior of a semiintegral bridge abutment under static and temperature-induced cyclic loading // Journal of Bridge Engineering. 2004. Vol. 9. № 2. P. 193–199.
16. Humphrey D., Blumenthal M. The use of tire-derived aggregate in road construction applications // Proceedings of the 1-st Conference “T&DI Green Streets & Highways”. ASCE, 2011.
17. Humphrey D. Civil engineering applications using tire derived aggregate (TDA). DRRR-2011?038. California: California Integrated Waste Management Board, 2010.
18. Mitoulis S., Palaiochorinou A., Georgiadis I., Argyroudis S. Extending the application of integral frame abutment bridges in earthquake prone areas by using novel isolators of recycled materials // Earthquake Engineering and Structural Dynamics. 2016. Vol. 45. № 14. P. 2283–2301.
19. Senetakis K., Anastasiadis A., Pitilakis K., Souli A. Dynamic behaviour of sand/rubber mixtures. Part II. Effect of rubber content on G/Go-г-DT curves and volumetric threshold strain // Journal of ASTM International. 2012. Vol. 9. № 2. Paper ID JAI103711.
20. Senetakis K., Anastasiadis A., Pitilakis K. Dynamic properties of dry sand/rubber (SRM) and gravel/rubber (GRM) mixtures in a wide range of shearing strain amplitudes // Soil Dynamics and Earthquake Engineering. 2012. Vol. 33. P. 38–53.
21. Argyroudis S., Kaynia A.M., Pitilakis K. Development of fragility functions for geotechnical constructions: application to cantilever retaining walls // Soil Dynamics and Earthquake Engineering. 2013. Vol. 50. P. 106–116.
22. CEN. EN 1998-1 Design of structures for earthquake resistance/. art 1: General rules, seismic actions and rules for buildings, European Committee for Standardization, Brussels, 2004.
23. PLAXIS 2D. Version 8. Reference Manual. 2008.
24. Argyroudis S.A., Mitoulis S.A., Pitilakis K.D. Seismic response of bridge abutments on surface foundation subjected to collision forces // Proceedings of the 4-th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN), Kos Island, Greece, 12–14 June 2013.
25. Mitoulis S., Argyroudis S., Kowalsky M. Evaluation of the stiffness and damping of abutments to extend direct displacement based design to the design of integral bridges // Proceedings of the 5-th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN), Crete Island, Greece, 25–27 May 2015.
26. CEN. EN 1998-2 Eurocode 8. Design of structures for earthquake resistance. Bridges. Brussels: European Committee for Standardization, 2005.
27. Maruri R., Petro S. Integral Abutments and Jointless Bridges // 2004 Survey Summary. Morgantown, W.V., USA: Federal Highway Administration and Constructed Facilities Center at West Virginia University, 2004.
28. Lafave J.M., Riddle J.K., Jarrett M.W., Wright B.A., Savatora J.S., An H., Fahnestock P.E. Numerical simulations of steel integral abutment bridges under thermal loading // ASCE Journal of Bridge Engineering. 2016. Vol. 21. № 10.