Определение угла дилатансии в приборах трехосного сжатия

Все дисперсные среды, в том числе грунты, обладают уникальным механическим свойством - дилатансией. Это свойство выражается в увеличении объема при сдвиговом деформировании и объясняется особенностями взаимного смещения твердых частиц. Если наблюдается уменьшение объема, используют термин «контракция» или «отрицательная дилатансия».

Из экспериментальных данных хорошо известно, что изменение «знака» дилатансии зависит от степени приближения дисперсной среды к критической плотности с_crit (или критическому коэффициенту пористости e_crit), которую имеет среда при сформировавшихся поверхностях скольжения и протекающих сдвигах. В случае если изначально среда была недоуплотнена, будет наблюдаться контракция, в случае исходно плотного сложения - дилатансия.

Дилатансия как механическое явление была описана в 1885 г. О. Рейнольдсом, однако одним из первых исследователей этого вопроса был D.W. Taylor, опубликовавший в 30-х годах XX в. серию работ, общие итоги которых подведены в учебнике механики грунтов 1948 года. Но наиболее известной публикацией в области исследования дилатансии является работа P.W. Rowe, изданная в 1962 году и содержащая общую теорию дилатансии. В соответствии с теорией Rowe, связь между объемной и сдвиговой деформацией для дилатирующей среды выражается следующим образом:

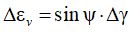
где Δε_v - объемная деформация грунта, ψ - угол дилатансии, Δγ - приращение угловой деформации.

Наиболее практически важным выводом в работе P.W. Rowe является количественная оценка изменения сопротивления сдвигу при ограниченной дилатансии дисперсной среды. Очевидно, что при свободном объемном деформировании будет наблюдаться уплотнение или разуплотнение грунта при сдвиге. Но в условиях реального основания объемное деформирование грунта чаще всего ограничено, и вместо приращения объемных деформаций наблюдается увеличение среднего напряжения, в свою очередь приводящего к увеличению сопротивления сдвигу. Rowe предлагает использовать вместо фиксированной величины угла внутреннего трения его переменное значение в зависимости от степени развития дилатансии (а, следовательно, и степени приближения к состоянию предельного равновесия).

На основании обширных лабораторных экспериментов М.D. Bolton, были получены корреляционные зависимости между пиковым и критическим значениями угла внутреннего трения, а также степенью плотности I_D. Показано, что для плотных грунтов угол дилатансии может достигать 15°, что позволяет существенно увеличить прочность. Из этих исследований следует, что угол дилатансии является комплексным параметром, на величину которого оказывают влияние физические характеристики (плотность сложения), деформационные (объемная сжимаемость) и прочностные (сопротивление сдвигу). Это сильно затрудняет лабораторную оценку, так как величина параметра меняется в зависимости от способа и режима определения.

В качестве обобщения зарубежного опыта исследований дилатансии можно рассматривать работу Vermeer и De Borst, в которой приведены наиболее важные выводы, полученные исследователями на протяжении 50 лет.

Изучением явления дилатансии занимались и отечественные специалисты. Результаты фундаментальных исследований явления дилатансии приведены в работах С.В. Бакушева, Г.Г. Болдырева, М.В. Малышева, Д.Ю. Соболевского. В них рассматриваются физический и механический смысл данного параметра, модификации теорий пластичности.

Необходимо отметить, что абсолютное большинство исследований дилатансии, а также методы ее количественной оценки относятся к песчаным грунтам. Это объясняется как бОльшим размером отдельных частиц, так и их формой. Характерная пластинчатая форма частиц глинистых грунтов не приводит к дополнительным объемным деформациям при сдвиге в связи с более высокой пористостью и возможностью относительного поворота отдельных частиц. В результате объемные деформации при сдвиге имеют настолько незначительную величину, что их измерение в ходе лабораторных исследований крайне затруднено. Этим объясняются рекомендации исследователей принимать для нормально уплотненных грунтов значение угла дилатансии равным нулю. В то же время в переуплотненных грунтах возможно образование агрегированных частиц, достаточно жестких, чтобы реализовывался механизм дилатансии.

Угол дилатансии используется в теории пластичности для учета объемного деформирования при пластическом течении. Это решение было предложено в работе Drucker и Prager, посвященной закону неассоциированного течения для дисперсных грунтов. Помимо поверхности текучести, определяемой законом Мора-Кулона, дополнительно вводится вторая поверхность - потенциал пластичности, наклон которой определяется углом дилатансии. В случае если угол дилатансии ψ равен углу внутреннего трения φ, поверхность текучести одновременно рассматривается как потенциальная поверхность (g = f), т.е. действует ассоциированный закон течения. Для большинства грунтов в этом случае возникают нереалистично большие объемные деформации, а реальный угол дилатансии обычно в разы меньше угла внутреннего трения. При указании ψ < φ модель использует неассоциированный закон течения, а при ψ = 0 объемные деформации при сдвиге будут отсутствовать (потенциал пластичности становится горизонтальной линией).

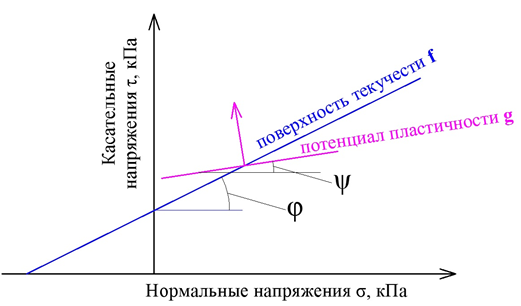
Все эти положения вошли в современные математические модели, использующие условие прочности Кулона-Мора - модель упрочняющегося грунта и ее производные (Hardening Soil, Hardening Soil Small-strain), модель слабого грунта и ее производные (Soft soil, Soft Soil Creep). Таким образом, в практике численного моделирования использование реального значения угла дилатансии позволяет мобилизовать дополнительное сопротивление сдвигу для грунтов с высокой плотностью - в основаниях нагруженных сооружений, насыпях и дамбах, что приводит к заметному экономическому эффекту и более полному использованию несущей способности грунта.

На основании физического смысла в практике инженерных изысканий угол дилатансии может быть определен в любом приборе, позволяющем реализовать измерение объемных деформаций грунтов при существенном развитии деформаций сдвига, в частности в приборах трехосного сжатия.

В ходе девиаторного нагружения образца регистрируется изменение объема вследствие дилатансии. В актуализированную редакцию ГОСТ 12248.3 включено рекомендуемое приложение К, в котором приведена простая методика определения угла дилатансии. Максимальная дилатансия проявляется обычно при пиковой прочности образца, следовательно, для ее определения необходимо выбирать диапазон объемных и сдвиговых деформаций, близкий к максимальному значению девиатора. Для условий трехосного сжатия по предложению P.A. Vermeer и R. De Borst угол дилатансии может быть определен по формуле:

Как и в прочих случаях, в данной формуле необходимо соблюдать правило знаков: приращение относительных вертикальных деформаций имеет отрицательную величину, а объемных - положительную при дилатансии и отрицательную при контракции.

Графически определение угла дилатансии выполняется по графику зависимости объемных деформаций от осевых в точке, соответствующей пиковой прочности либо на участке максимального наклона.

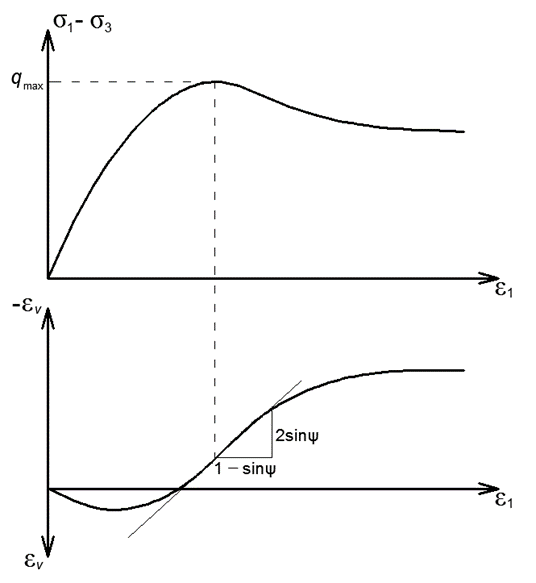
На графике хорошо видно, что на начальном этапе приложения девиаторной нагрузки идет доуплотнение образца (за счет возрастающего среднего напряжения), однако впоследствии объемные деформации стабилизируются, а в случае дилатирующих грунтов может наблюдаться объемное расширение. Очевидно, что такое представление имеет смысл исключительно для испытаний по схеме КД, так как схемы КН и НН предполагают постоянство объемных деформаций.

Достоинством метода является его высокая чувствительность: определение угла дилатансии возможно даже для супесчаных и глинистых грунтов. Кроме того, данные испытания чаще всего выполняются, если предполагается использование численных методов расчета, а определение угла дилатансии может быть выполнено по результатам того же испытания, без увеличения сметной стоимости и числа необходимых образцов, так как отдельного опыта не требуется.

ООО «НПП Геотек» предлагает автоматизированный испытательный комплекс «АСИС Про» для осесимметричных КД трехосных испытаний образцов грунта с возможностью высокоточного измерения деформаций объема при сдвиге. В состав комплекса входят камеры трехосного сжатия, необходимое оборудование для создания вертикального силового воздействия, управления камерным и противодавлением. Испытания проводятся в автоматизированном режиме с контролем всех параметров испытания в режиме реального времени.

Более подробную техническую информацию можно получить у специалистов компании или на сайте www.npp-geotek.ru.

Список литературы

1. Бакушев С.В. Модифицированная деформационная теория пластичности сыпучей среды. Строительная механика и расчет сооружений, № 2, 2018.
2. Болдырев Г.Г. Методы определения механических свойств грунтов с комментариями к ГОСТ 12248-2010. М.: ООО «Прондо», 2014.
3. Малышев М.В. Прочность грунтов и устойчивость оснований сооружений. М.: Стройиздат, 1994.
4. Соболевский Д.Ю. Прочность и несущая способность дилатирующего грунта. Минск: Наука и техника, 1994.
5. Bolton M.D. The strength and dilatancy of sands. Geotechnique, Vol. 36, No. 1, 1986.
6. Drucker D.C., Prager W. Soil mechanics and plastic analysis for limit design. Quarterly of Applied Mathematics, Vol. 10, No. 2, 1952.
7. Rowe P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proceedings of the Royal Society of London. Series A, Vol. 269, 1962.
8. Taylor D.W. Fundamentals of Soil Mechanics. John Wiley and Sons, Inc., New York, 1948.
9. Vermeer P.A., De Borst R. Non-associated plasticity for soils, concrete and rock. Heron, Vol. 29, No. 3, 1984.