Вильям Паури о прессиометрических испытаниях

11.3.3. ПРЕССИОМЕТРИЧЕСКИЕ ИСПЫТАНИЯ

 

А. Общее описание

 

Прессиометр представляет собой цилиндрическое устройство, предназначенное для приложения равномерного радиального давления к стенкам скважины, в которую оно помещается. Существует два основных типа прессиометров:

• прессиометр Менарда (баллонный прессиометр), который опускается в предварительно пробуренную скважину;
• самозабуривающийся прессиометр, который сам пробуривает скважину и таким образом меньше нарушает грунт до начала испытания.

 

В обоих случаях испытание с помощью прессиометра включает приложение известной нагрузки (давления) на грунт и измерение его результирующей деформации. Следовательно, интерпретация параметров, измеренных при таких испытаниях, в техническом отношении не основывается на эмпирических корреляциях. В связи с этим результаты прессиометрических тестов отличаются от данных стандартных испытаний на пенетрацию (SPT) и испытаний коническим зондом (CPT), то есть от данных динамического и статического зондирования соответственно.

Схематическое представление основных особенностей устройства прессиометра приведено на рисунке 11.11.

 

 

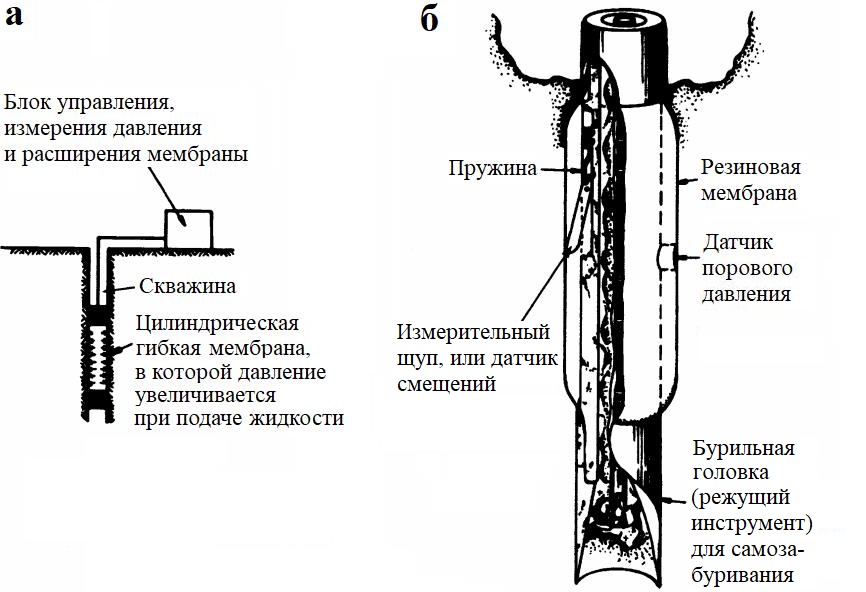
Стенки ствола скважины нагружаются путем создания давления жидкости, содержащейся внутри гибкой резиновой мембраны. Снаружи эта мембрана обычно защищена стальными лентами. Расширение полости внутри нее (рабочей камеры прессиометра) определяется либо путем измерения объема жидкости, необходимой для повышения давления на мембрану, либо путем измерения смещения грунта, прилегающего к наружной стенке камеры, непосредственно с помощью измерительных щупов или индуктивных датчиков смещений LVDT (либо и того, и другого). Обычно используются три измерительных щупа или три индуктивных датчика смещений, расположенных в одной горизонтальной плоскости на угловом расстоянии 120 град. друг от друга.

Как правило, прессиометры рассчитаны на максимальное давление при заполнении жидкостью в диапазоне 2,5–10 МПа в рыхлых дисперсных грунтах и 10–20 МПа в твердых дисперсных грунтах и в слабых скальных породах.

Интерпретация данных прессиометрических испытаний основана на анализе расширяющейся цилиндрической рабочей камеры с деформацией только в горизонтальной плоскости. Следовательно, длина расширяющейся части прессиометра должна быть по крайней мере в шесть раз больше ее диаметра, чтобы избежать значительных концевых эффектов.

Необходимо вносить поправки в результаты измерений давления, объема и деформации рабочей камеры, чтобы учесть сжимаемость жидкости и трубопроводов, разницу в высоте прибора и датчика давления, а также жесткость мембраны. Ошибки в измерениях изменений объема из-за расширения трубопровода и сжатия жидкости, вероятно, будут наиболее значительными в полутвердых дисперсных грунтах. Потеря давления (когда давление, фактически прикладываемое к грунту, меньше давления внутри рабочей камеры из-за жесткости мембраны), вероятно, будет наиболее значительной в слабых дисперсных грунтах. Процедуры калибровки, которые должны быть выполнены для количественной оценки этих эффектов, описаны в работе Мэйра и Вуда 1987 года (Mair R.J., Wood D.M. Pressuremeter Testing: Methods and Interpretation // Construction Industry Research & Information. London: Association/Butterworths, 1987).

Откорректированные данные прессиометрического испытания представляются в виде графика зависимости давления в рабочей камере прессиометра р от увеличения объема камеры ΔV или ее относительной деформации ε_c, как показано на рисунке 11.12. Деформация камеры ε_c определяется как смещение наружу ее стенки γ_c, поделенное на ее исходный радиус (то есть радиус в начале прессиометрического испытания) ρ₀. В подразделе 11.3.3, Б показано, что для небольших деформаций она примерно равна половине относительного увеличения объема камеры, то есть ε_c=γ_c/ρ₀≈0,5ΔV/V₀, где V₀ – начальный объем полости рабочей камеры.

 

 

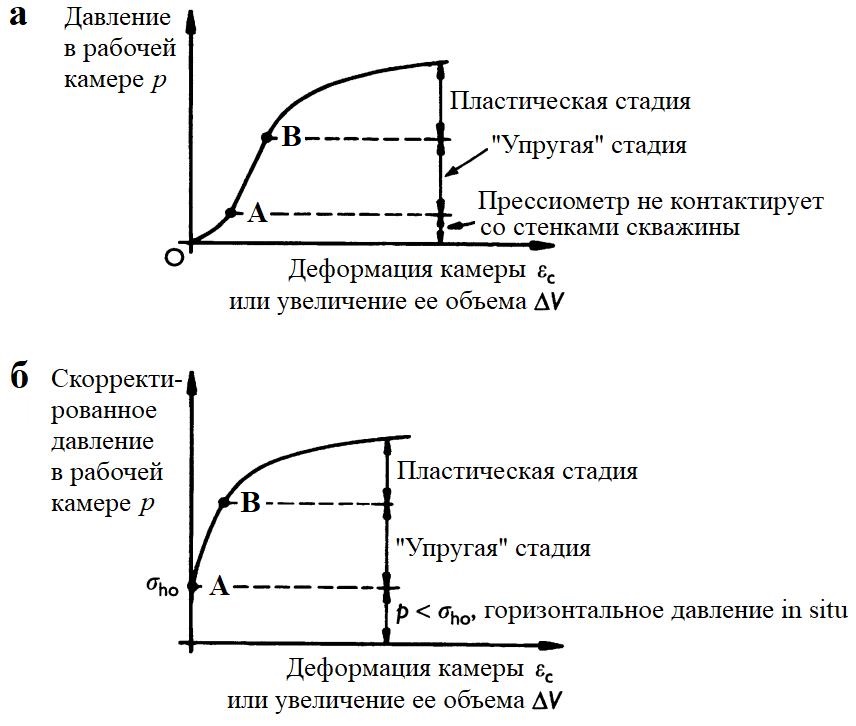
Как уже упоминалось, основное различие между прессиометром Менарда и самозабуривающимся прессиометром состоит в том, что первый опускается в предварительно пробуренную скважину – следовательно, неизбежны некоторые нарушения грунта, а в начале испытания прибор, вероятно, не будет соприкасаться со стенками скважины. Эта разница отражается на данных, полученных на ранних этапах испытания – до того, как прессиометр Менарда начнет контактировать со стенками скважины.

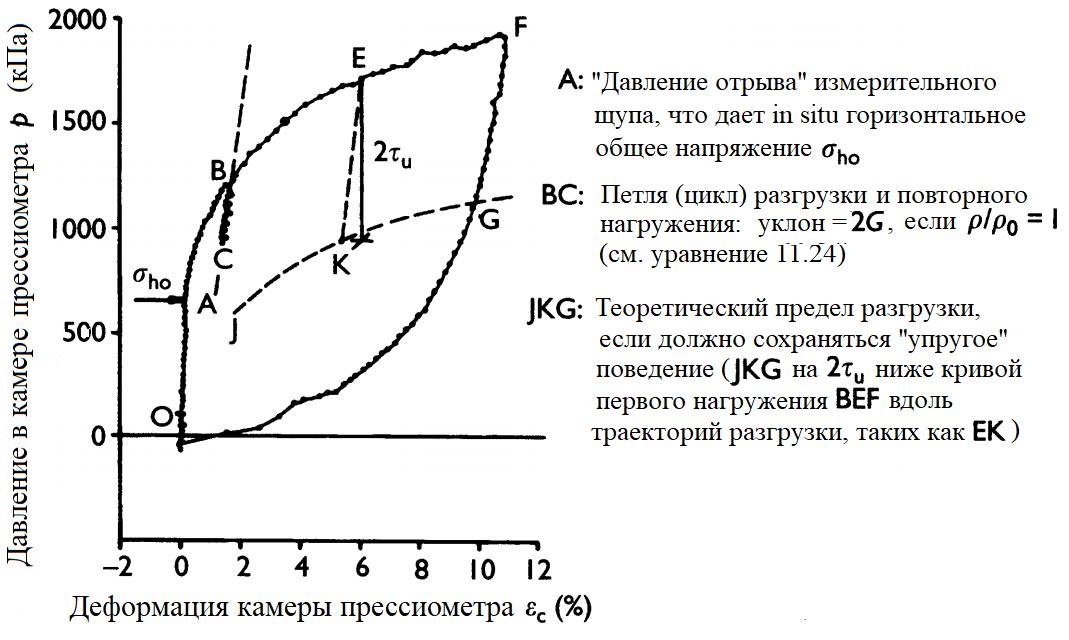
При испытании с использованием прессиометра Менарда (см. рис. 11.12, а) кривая «напряжение – деформация» должна резко увеличивать свою крутизну в точке A, когда прибор начинает контактировать с предварительно сформированной стенкой скважины и давить на любой ослабленный грунт. Если грунт не является нормально уплотненной глиной, связь между ростом давления и увеличением деформации камеры будет приблизительно линейной, пока не будет достигнута точка B, в которой грунт стенки скважины начинает пластически деформироваться. При дальнейшем повышении давления в камере прессиометра пластическая зона распространяется дальше в окружающий грунт, пока в конечном итоге не будет достигнуто некоторое предельное давление p_L.

При высококачественном испытании самозабуривающимся прессиометром скорректированная кривая «давления – объем» должна начинаться с момента контакта прессиометра со стенками скважины. Не должно быть никакого ослабления или нарушения окружающего грунта. В идеале не должно быть увеличения объема рабочей камеры до тех пор, пока давление в ней не превысит общее горизонтальное напряжение в грунте in situ σ_ho. Следовательно, полное горизонтальное напряжение in situ можно определить по точке A (см. рис. 11.12, б), начиная с которой объем камеры начинает значительно увеличиваться с ростом давления. В самозабуривающемся прессиометре, который определяет увеличение объема рабочей камеры с помощью содержащихся в нем датчиков смещений, каждый датчик может давать различные величины «давления отрыва» (давления в камере, при котором датчик смещений (или измерительный щуп) начинает показывать значительное смещение; причем можно было бы ожидать, что при испытании самозабуривающимся прессиометром это давление будет равно горизонтальному напряжению в грунте in situ). Поэтому оценка общего горизонтального напряжения in situ, полученного по данным испытаний, требует внимания и опыта.

После превышения эффективного горизонтального напряжения in situ объем камеры должен увеличиваться приблизительно линейно с ростом приложенного давления до тех пор, пока грунт на стенке скважины не начнет пластически деформироваться в точке B. В действительности «линейная» часть графика AB может быть очень короткой или почти не существовать (забегая вперед, см. рис. 11.15, откуда видно, что то же самое верно и для испытания прессиометром Менарда). При дальнейшем увеличении давления в камере радиус «пластической» зоны увеличивается до тех пор, пока в конечном итоге не будет достигнуто предельное давление p_L.

По данным испытаний прессиометром Менарда оценить общее горизонтальное напряжение in situ непросто из-за нарушения и ослабления грунта на стенке скважины. Даже если точка A (см. рис. 11.12, a) соответствует устройству, контактирующему с неповрежденным грунтом на стенке скважины, это не может быть принято как показатель горизонтального напряжения in situ, потому что грунт в точке A нагружается начиная не с состояния in situ, а с ненагруженного состояния после установки прессиометра. Мэйр и Вуд в своей работе 1987 года (Mair R.J., Wood D.M. Pressuremeter Testing: Methods and Interpretation // Construction Industry Research & Information. London: Association/Butterworths, 1987) описали итерационную процедуру, предложенную Марслэндом и Рэндольфом в 1977 году (Marsland A., Randolph M.F. Comparisons of the results from pressuremeter tests and large in situ plate tests in London Clay // Geotechnique. 1977. Vol. 27. № 2. P. 217–243), которая может быть использована для оценки общего горизонтального напряжения in situ по результатам испытаний с использованием прессиометра Менарда в переуплотненных высокопластичных глинах (таких как «лондонская глина»), которые ведут себя приблизительно упруго во время начального нагружения.

В дополнение к полному горизонтальному напряжению in situ график «давление в камере – ее деформация» может использоваться для оценки модуля сдвига грунта, прочности глины на недренированный сдвиг, а также пиковой прочности и угла дилатансии ψ песка. Включив в устройство датчики порового давления воды, можно также измерить коэффициент консолидации в горизонтальном направлении c_h (который определяет уплотнение из-за горизонтальной деформации при горизонтальной фильтрации) и угол внутреннего трения ϕ' для глин. В настоящем обсуждении мы сосредоточимся на наиболее распространенных приложениях, а именно на определении полного горизонтального напряжения in situ и модуля сдвига, а также прочности глин на недренированный сдвиг. Детали процедур, используемых для определения других параметров, приводятся в работе Мэйра и Вуда 1987 года (Mair R.J., Wood D.M. Pressuremeter Testing: Methods and Interpretation // Construction Industry Research & Information. London: Association/Butterworths, 1987).

 

Б. Анализ напряжений

 

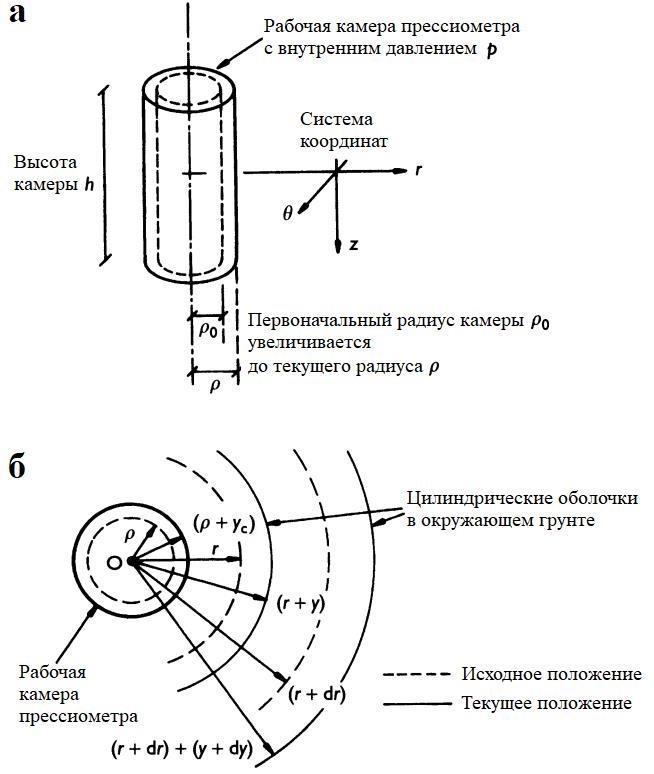
Интерпретация данных испытаний прессиометром основана на анализе расширяющейся цилиндрической камеры в неограниченном грунтовом массиве. Принимается, что деформация грунта происходит в горизонтальной плоскости (рис. 11.13, а), в то время как общее вертикальное напряжение σ_z остается постоянным. Следует отметить, что такие же результаты получаются, если изначально принимается, что равна нулю вертикальная деформация ε_z (а не вертикальный прирост полного напряжения Δσ_z).

Если давление в рабочей камере вырастает на величину Δp, радиус камеры увеличивается на величину γ_c от своего начального значения ρ (то есть от его значения до приложения прироста давления в камере Δp). В грунте вне камеры общая цилиндрическая оболочка с начальным радиусом r выталкивается наружу до нового радиуса (r+γ), как показано на поперечном разрезе на рисунке 11.13, б. Аналогичным образом цилиндрическая оболочка в окружающем грунте немного дальше от оси камеры с начальным радиусом (r+dr) выталкивается до нового радиуса [(r+dr)+(γ+dγ)].

 

 

Приращение относительной радиальной деформации Δε_r при радиусе r определяется следующим образом: Δε_r = (изменение радиального расстояния между оболочками) / (начальное радиальное расстояние между оболочками).

Из рисунка 11.13, б видно, что:

 

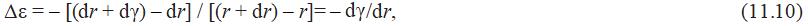
где отрицательный знак показывает, что для значения γ (см. рис. 11.13, б), приращение радиальной деформации является растягивающим.

 

Приращение относительной тангенциальной деформации Δε_θ при радиусе r определяется следующим образом: Δε_θ = (изменение длины окружности) / (начальная длина окружности).

Из рисунка 11.13, б видно, что:

 

где отрицательный знак показывает, что для значения γ (см. рис. 11.13, б) тангенциальная деформация является растягивающей.

 

Если грунт может быть идеализирован как однородный изотропный линейно-упругий материал, который подчиняется закону Гука, то уравнения (6.1) из раздела 6.2.2

 

 

можно представить в терминах общего главного напряжения и приращений деформации в радиальном (r), круговом (θ) и вертикальном (z) направлениях:

 

 

Но Δσ_z=0 (потому что величина σ_z является постоянной), поэтому:

 

 

Объединив уравнения (11.13а) и (11.13б) для устранения Δσ_θ, получим:

 

 

Сходным образом, объединив уравнения (11.13б) и (11.13а) для устранения Δσ_r, можно записать:

 

 

Таким образом, мы получили приращения радиального и тангенциального напряжений (Δσ_r и Δσ_θ соответственно) в терминах недренированных упругих показателей для общего напряжения – E_u (модуля Юнга) и v_u (коэффициента Пуассона), а также приращения радиальной и тангенциальной деформаций (Δε_r и  Δε_θ соответственно).

Уравнение равновесия для кольцевого сегмента – такое же, как и при анализе тоннеля в разделе 10.11, за исключением того, что сила тяжести теперь действует вне рассматриваемой плоскости, то есть перпендикулярно ей, а не в ней, как в случае горизонтального тоннеля. Удалив из уравнения (10.17) из раздела 10.11.1

 

 

такой член математического выражения, как удельный вес, и записав уравнение (10.17) в терминах приращений напряжений Δσ_r и Δσ_θ (а не напряжений σ_r и σ_θ), получим следующее уравнение равновесия:

 

 

Подставив выражения для Δε_r из уравнения (11.10) и для Δε_θ из уравнения (11.11) в уравнения (11.14), получим:

 

 

 

Подставив уравнения (11.16) в уравнение (11.15), видим, что выражение [E_u/(1-v_u²)] появляется с обеих сторон, поэтому оно отбрасывается:

 

 

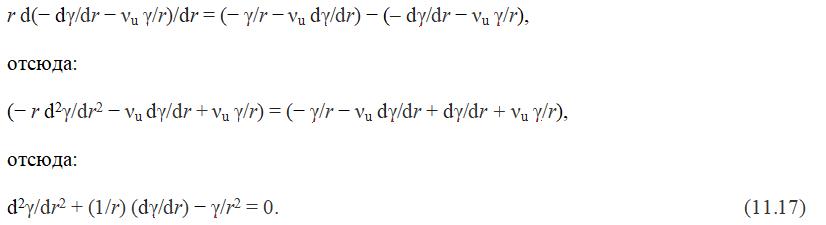
Уравнение (11.17) является дифференциальным c единственной пременной γ. Его общее решение, которое может быть проверено путем подстановок, таково:

 

 

При прессиометрическом испытании значение константы A может быть определено, поскольку радиальное перемещение стенки рабочей камеры γ_c измеряется или может быть выведено из изменения объема камеры:

 

 

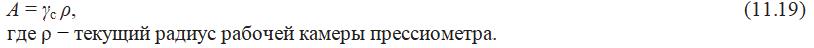
В качестве альтернативы, определив деформацию камеры как ε_c=γ_c/ρ₀ (где ρ₀ - радиус камеры в начале прессиометрического испытания), получим:

 

 

Подстановка уравнения (11.20) в уравнения (11.10) и (11.11) дает следующие выражения для радиальных и тангенциальных деформаций (измеренных начиная с нуля в начале прессиометрического испытания, чтобы можно было отбросить обозначение «приращение деформации»):

 

 

Подстановка уравнений (11.21) в уравнения (11.14) дает следующие выражения для радиального и тангенциального приращений полного напряжения:

 

 

Из уравнения (6.6) из раздела 6.2.2

 

 

можно получить, что

 

 

Этот результат примечателен в двух отношениях.

1. Подстановка уравнений (11.22) в уравнение (11.12в) при Δσ_z=0 показывает, что ε_z=0, поэтому вся деформация происходит в горизонтальной плоскости. Вертикальная деформация равно нулю, в то время как вертикальное напряжение остается постоянным.

2. При расширении рабочей камеры прессиометра окружающий грунт деформируется при постоянном объеме. Это связано с тем, что радиальные и тангенциальные деформации равны по модулю и противоположны, а вертикальная деформация равна нулю. Кроме того, нет никакого изменения среднего полного напряжения p, потому что вертикальное полное напряжение остается постоянным, в то время как увеличение радиального полного напряжения Δσ_r точно противоположно уменьшению тангенциального полного напряжения Δσ_θ. Это означает, что если поведение грунта является приблизительно изотропным и упругим, то при постоянном среднем эффективном напряжении p' имеет место деформация при постоянном объеме, а в поровом давлении изменений не происходит. Расширение полости – это исключительно процесс сдвига, а не процесс сжатия, как могло бы показаться на первый взгляд.

 

У стенки рабочей камеры увеличение радиального полного напряжения Δσ_r равно увеличению давления в камере Δp. Подставляя r=ρ, (текущий радиус полости) в уравнение (11.23а), получим:

 

 

В начале испытания радиус камеры ρ равен ее начальному радиусу ρ₀, что дает ρ/ρ₀=1 и

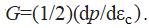
Однако обычно измеряют модуль сдвига во время цикла «разгрузка – повторное нагружение» (например, забегая вперед, см. рис. 11.15), чтобы гарантировать, что весь грунт деформируется приблизительно упруго. В этом случае коэффициент ρ/ρ₀ будет значительным, если деформация полости в начале цикла «разгрузка – повторное нагружение» сравнительно велика.

Вторая причина для определения модуля сдвига по циклу «разгрузка – повторное нагружение» состоит в том, чтобы избежать влияния нарушений грунта, вызываемых установкой прессиометра. Некоторое нарушение при установке почти неизбежно (даже при работе с самозабуривающимся прессиометром).

В качестве альтернативы деформации рабочей камеры ε_с данные прессиометрических испытаний могут быть представлены в терминах изменений ее объема ΔV. При увеличении ее радиуса от ρ до (ρ+Δγ_c) ее объем увеличивается от πρ²h до π(ρ+Δγ_c)²h, где h – высота камеры. Таким образом, относительное увеличение объема (рассчитанное с учетом текущего объема камеры) можно представить следующим образом:

 

 

И, подставляя полученное выражение для dε_c в уравнение (11.24), получим:

 

 

При определении модуля сдвига по циклу «разгрузка – повторное нагружение» величина цикла напряжений (цикла нагрузки) должна быть достаточно малой, чтобы поведение грунта оставалось приблизительно упругим, а пластическое течение (пластическое деформирование) при разгрузке не начиналось. Рассмотрение круга полных напряжений Мора (рис. 11.14) показывает, что начиная с состояния in situ, когда σ_r=σ_θ=σ_ho, напряжение сдвига в стенке камеры при давлении в полости (σ_ho+Δp) определяется следующим образом:

 

 

 

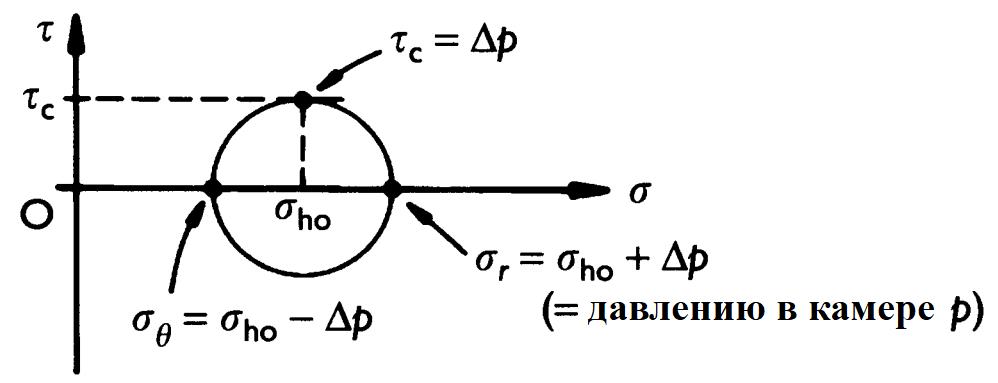
Идеальный глинистый грунт начнет пластически деформироваться, когда напряжение сдвига камеры τ_c достигнет прочности материала на недренированный сдвиг τ_u, то есть при

 

 

Поэтому пластическое поведение начнет проявляться при давлении в камере p_p, где

 

 

После этого момента упругое решение для напряжений и деформаций не имеет силы. Когда давление в камере увеличивается, пластическая зона распространяется наружу в окружающий грунт.

Если давление в камере было увеличено в достаточной степени, чтобы вызвать разрушение грунта в стенке скважины (то есть до значения p=p_p=σ_ho+τ_u), поведение грунта при разгрузке будет упругим до тех пор, пока давление в камере не будет уменьшено до такой степени, чтобы напряжение сдвига на стенке скважины было равно τ_u в противоположном направлении (по знаку), то есть пока не будет соблюдено равенство p=(σ_ho – τ_u). Таким образом, снижение давления в камере во время цикла «разгрузка – повторное нагружение» не должно превышать 2τ_u, чтобы поведение грунта оставалось приблизительно упругим. Этот предел величины цикла «разгрузка – повторное нагружение», выполняемого для измерения модуля сдвига G, показан на рисунке 11.15, который иллюстрирует интерпретацию данных, полученных по результатам хорошо выполненного испытания прессиометром.

 

 

 

Прочность глины на недренированный сдвиг можно оценить по зависимости между давлением в рабочей камере прессиометра и ее объемом после начала пластической деформации (то есть при давлении в камере р>σ_ho+τ_u). На главном этапе прессиометрического испытания при р>σ_ho+τ_u кольцевая зона грунта вокруг камеры с внешним радиусом r_p разрушается, при этом:

 

 

Следует обратить внимание, что σ_r>σ_θ (рис. 11.16), поскольку камера расширяется в окружающий грунт. Это противоречит результатам анализа тоннеля с круглым сечением, выполненного в разделе 10.11, поскольку в случае тоннеля окружающий грунт при разрушении обваливается в полость.

 

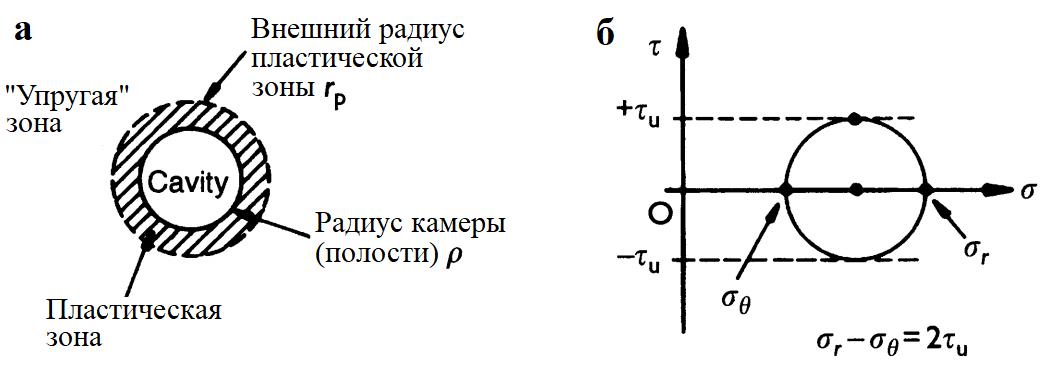
Рис. 11.16. Пластическая и упругая зоны вокруг прессиометра на основном этапе испытаний, то есть при p>σ_ho+τ_u (а) и круг Мора для  полного напряжения в пластической зоне (б).

 

При подстановке уравнения (11.30) в уравнение (11.15) условие равновесия в пластической зоне становится следующим:

 

 

что может быть следующим образом перегруппировано и проинтегрировано между пределами σ_r=p (текущим давлением, действующим на стенку камеры прессиометра с радиусом r=ρ) и σ_r=σ_ho+τ_u (чего достаточно, чтобы вызвать пластическое поведение) на внешней границе пластической зоны, которая имеет радиус r=r_p:

 

 

Теперь надо найти r_p – внешний радиус пластической области. Внутри нее взаимосвязь между радиусом r и смещением γ, определяемая уравнениями (11.18) и (11.20), непригодна, поскольку уравнение (11.18) было получено в предположении, что материал ведет себя упруго, подчиняясь закону Гука. Однако, если пластическая зона деформируется при постоянном объеме, мы можем сказать, что объем грунта, который теперь занимает кольцевую зону с внутренним радиусом ρ и внешним радиусом r_p, первоначально занимал кольцевую зону с внутренним радиусом (ρ–γ_c) и внешним радиусом (r_p–γ_rp) (напомним, что r_p – текущий радиус края пластической зоны; γ_rp – его радиальное смещение наружу от исходного положения; ρ – текущий радиус полости камеры прессиометра; γ_с – его увеличение по сравнению с исходным положением). Приравнивая эти два объема друг к другу, для камеры высотой h получим:

 

 

Сразу за пределами пластической зоны упругие взаимосвязи все еще пригодны. В частности:

 

 

Объединение уравнений (11.33) и (11.34) для исключения γ_rp дает:

 

 

Подставив уравнение (11.35) в уравнение (11.32) и вспомнив, что

 

 

Смысл уравнения (11.36б) состоит в том, что во время пластической фазы прессиометрического испытания график зависимости давления в камере p от натурального логарифма относительного изменения объема камеры ΔV/V должен иметь наклон τ_u. Кроме того, если эта линия проецируется на точку ln(ΔV/V)=0 (что соответствует ΔV/V=1), соответствующее значение p равно p_L, где:

 

 

что дает дополнительную проверку значений G и τ_u, определенных с помощью уравнений (11.24) или (11.26) и (11.36б).

 

Приведенный выше анализ испытания прессиометром взят в основном из работы Джибсона и Андерсона 1961 года (Gibson R.E., Anderson W.F. In situ measurement of soil properties with the pressuremeter // Civ Engng & Public Works Review. 1961. Vol. 56. № 658. P. 615–618). Эти авторы также представили аналогичный анализ прессиометрического испытания в песке в терминах эффективных напряжений и критерия прочности, обусловленной силами внутреннего трения: τ = σ' tg ϕ'.

Начиная с горизонтального эффективного напряжения in situ σ'_ho увеличение радиального эффективного напряжения Δσ'_r по мере роста давления в полости камеры равно по величине уменьшению тангенциального эффективного напряжения Δσ'_θ. Принимается, что нет никаких изменений в поровом давлении, так что все изменения в давлении в камере воспринимаются скелетом грунта как изменения в эффективном напряжении. При условии, что поведение материала, по существу, является упругим, это согласуется с деформацией при постоянном объеме, поскольку среднее эффективное напряжение s' остается тем же самым.

Из круга эффективных напряжений Мора, показанного на рисунке 11.17, видно, что увеличение давления в камере Δp_p, когда грунт на стенке скважины начинает разрушаться, определяется следующим образом:

 

 

Максимальное снижение давления в камере Δp_u/r,max затем можно применить в цикле «разгрузка – повторное нагружение», не вызывая разрушения грунта в противоположном по знаку направлении, то есть при σ'_θ>σ'_r оно определяется диаметром круга эффективного напряжения Мора, показанного на рисунке 11.17. Это потому, что по мере уменьшения σ'_r увеличивается σ'_θ на ту же величину. Круг эффективного напряжения Мора в начале пластического поведения при разрушении является, следовательно, таким же, как и в начале пластического поведения при расширении камеры с обратными значениями σ'_r и σ'_θ.

 

 

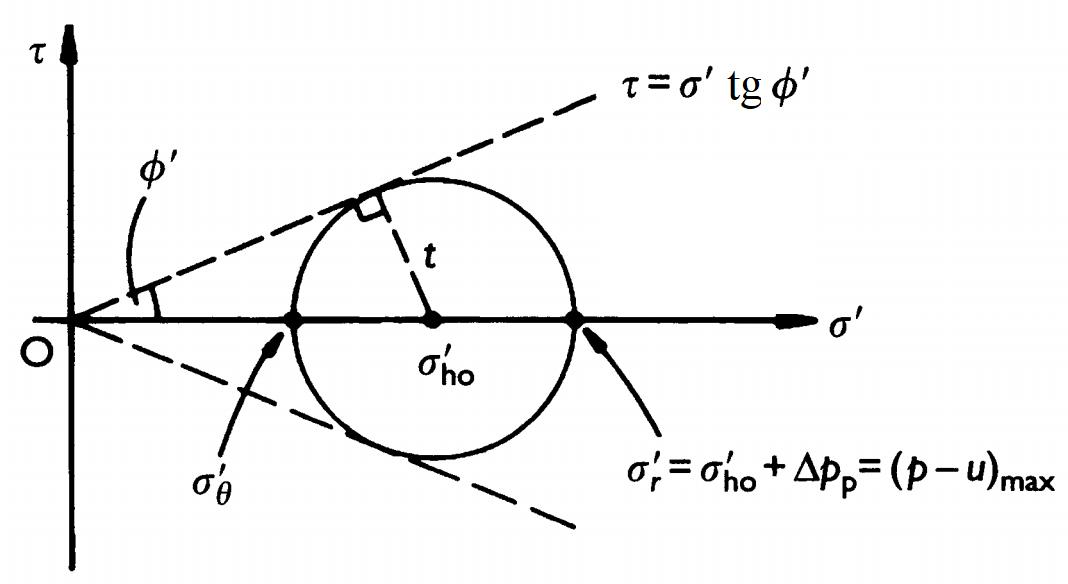
Следовательно:

 

 

Отсюда:

 

где p – давление в полости камеры; u – поровое давление в грунте на стенке скважины, соприкасающейся с камерой; (p–u)_max – максимальная разница между этими величинами.

 

Подставляя уравнение (11.40) в уравнение (11.39), чтобы исключить σ'_ho, получим:

 

 

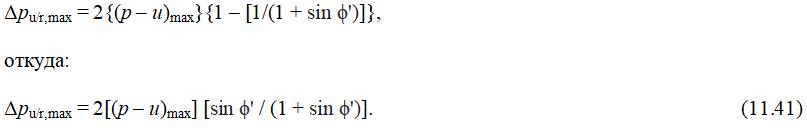
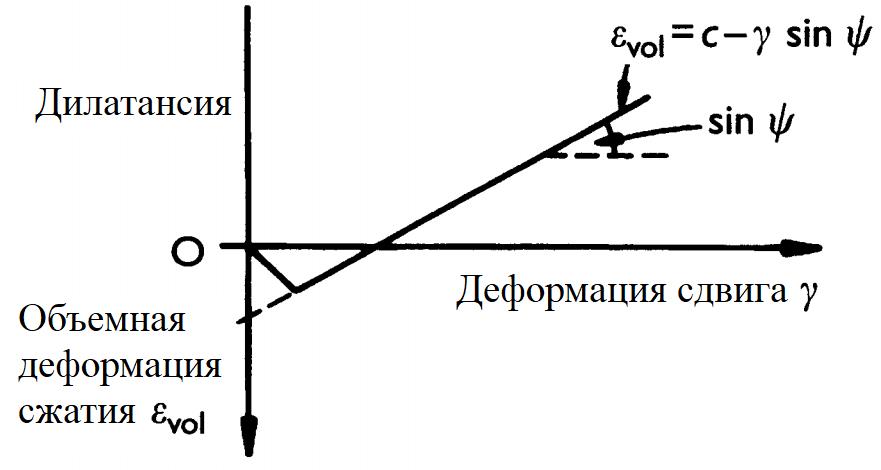
При прессиометрических испытаниях в глинах предположение о том, что сдвиг происходит при постоянном объеме, обычно является оправданным. Однако для песков это предположение менее реалистично, поскольку песок может сильно дилатировать, по крайней мере после начала его пластического поведения. Анализ, представленный Хьюзом с соавторами в 1977 году (Hughes J.M.O., Wroth C.P., Windle D. Pressuremeter tests in sands // Geotecbnique. 1977. Vol. 27. № 4. P. 455–477), учитывает влияние дилатансии путем использования идеализированной зависимости между объемной деформацией ε_vol и деформацией сдвига γ

 

где c является константой (рис. 11.18),

 

а также зависимости «напряжение – дилатансия», которая связывает углы внутреннего трения в пиковом и критическом состояниях и угол дилатансии ψ:

 

 

 

Уравнение (11.43) было первоначально предложено Роу в 1962 году (Rowe P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact // Proceedings of the Royal Society. London, 1962. Vol. A269. P. 500–527). Пример более простой эмпирической зависимости «напряжение – дилатансия», связывающей ϕ'_peak, ϕ'_crit и ψ, был дан в уравнении (2.14) по работе Болтона 1976 года (Bolton M.D. The strength and dilatancy of sands // Gйotechnique. 1986. Vol. 36. № 1. P. 65–78) из раздела 2.9:

 

 

В анализе, представленном Хьюзом с соавторами в 1977  году (Hughes J.M.O., Wroth C.P., Windle D. Pressuremeter tests in sands // Geotecbnique. 1977. Vol. 27. № 4. P. 455–477), принимается, что песок будет дилатировать неограниченно при постоянном пиковом угле внутреннего трения ϕ'_peak и постоянном угле дилатансии ψ.

Критерий разрушения τ = σ' tg ϕ' выражается в терминах пиковой прочности ϕ'_peak (как в уравнениях 11.38–11.41). Сделав эти допущения, Хьюз с соавторами показали, что после появления пластичности на стенке скважины давление в камере прессиометра р и ее деформация ε_c связаны следующим соотношением:

 

где A – константа; u₀ – начальное поровое давление in situ;

 

 

Если величина ε_c мала, то 1+ε_c≈1 и уравнение (11.44) принимает следующий вид:

 

 

тогда значение s может быть выведено из уклона графика зависимости ln(p–u₀) от ln(ε_c+c/2). Чтобы построить этот график, необходимо оценить значение константы c (см. рис. 11.18) для рассматриваемого песка.

Зависимость «напряжение – дилатансия» (уравнение (11.43)), может использоваться для исключения либо  ϕ'_peak, либо ψ из уравнения (11.45), давая после значительных алгебраических преобразований следующие уравнения:

 

 

---

Источник

1. Powrie W. Soil Mechanics. Concepts and Applications (3rd edition). New York – London: Taylor & Francis Group, 2014 (first published in 1997 by E&FN Spon). URL: taylorfrancis.com/books/mono/10.1201/9781315275284/soil-mechanics-william-powrie.