Беседа об инновациях и технологическом развитии СРТ. Часть 2

Интерпретация результатов статического зондирования – это, по сути дела, исследование состояния грунтов на основе представлений о типовых моделях, т.е. это интерактивное моделирование и сравнительный анализ полученных моделей с выходом на коррелятивные связи с расчётными геотехническими характеристиками.

При обсуждении проблем статического зондирования очень часто возникает иллюзия того, что в ходе зондирования непосредственно фиксируются грунты разного состава, состояния и свойств. На самом деле в процессе зондирования наблюдаются параметры взаимодействия зонда, как жёсткого металлического тела, насыщенного различными датчиками, с грунтовой средой, состояние которой непрерывно меняется. Программы записи результатов зондирования фиксируют эти изменения с определённой частотой.

Вопрос о размере рабочей зоны взаимодействия зонда и окружающих пород обсуждался с первых шагов развития метода статического зондирования. Сейчас можно считать установленным, что этот размер может изменяться в широких пределах от 15 диаметров зонда в жёстких прочных грунтах до 1 диаметра в слабых текучих грунтах [1,2,3,4]. Подобная реакция зонда зависит, прежде всего, от величины эффективных напряжений, действующих в рабочей зоне зонда, и в общем случае эта зона сжимается с ростом эффективных напряжений. В определённых условиях может происходить даже ошибочная интерпретация грунта, например, когда плотные пески при высоком уровне эффективных напряжений реагируют на внедрение зонда как пески рыхлого сложения.

Высказанные положения говорят о том, что правильная интерпретация данных зондирования в части распознавания типовых моделей грунтовой среды, через которую движется зонд, невозможна без соотнесения параметров зондирования и эффективных напряжений. Подобные связи могут быть выражены зональными графиками для нормализованных моделей поведения грунтов – normalized Soil Behaviour Type (SBT_n), основанных на применении откорректированных и нормализованных значений лобовых (Q_t) сопротивлений и коэффициента трения (F_r), когда учитывается величина порового давления u₂, замеренного с помощью датчика, расположенного непосредственно за конусным наконечником:

           (1)

          (2)

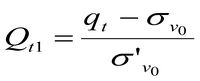
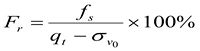
σ_v0 - общие вертикальные напряжения;

σ’_v0 - эффективные вертикальные напряжения.

Как было отмечено в первой части настоящей статьи, последние конструкции зондов имеют равноплощадные концы муфты трения, что позволяет производить корректировку замеров только лобовых сопротивлений (q_c → q_t), оставляя без изменений замеры боковых сопротивлений (f_s).

Поскольку очень часто зондирование применяется в неоднородных слоистых разрезах, возникает серьёзная проблема выделения и различения переходных зон для грунтов разного состава и свойств.

В общем случае нормализованное значение лобового сопротивления Qt_n можно выразить [5,6,7]:

     (3)

— безразмерная величина чистого сопротивления конуса;

— фактор нормализации напряжений;

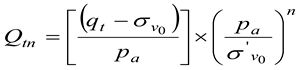
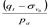
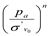
n — показатель степени, непосредственно связанный с типом грунта по SBT;

p_a — атмосферное давление, выраженное в тех же единицах, что q_t и σ_v0.

Соответственно, когда n = 1, Q_tn = Q_t1.

Значение экспоненты n в вышеприведённой формуле можно определить через типологический индекс грунта I_c:

        (4), где

(5)

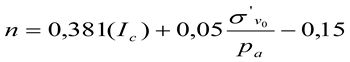
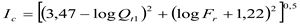
На основе нормализованных значений были построены многочисленные зональные диаграммы интерпретации и связи параметров зондирования с комплексными показателями состояния и деформирования грунтов [7]. Основная диаграмма отражает связь типологического индекса I_c и моделей грунтов в координатах приведённых значений лобового сопротивления и коэффициента трения (см. рис. 3 в первой части статьи).

Установленная зависимость позволяет не только различать основные типы грунтов, но и распознавать переходные зоны, где наблюдается определенное запаздывание реакции зонда на смену грунтов. Выделение переходных зон во время зондирования имеет большое практическое значение, особенно с точки зрения программного обеспечения процессов фиксации и интерпретации результатов зондирования в каждой точке. В зонах перехода от песчаных грунтов к глинистым типологический индекс грунта I_c будет иметь значение около 2,6 (Robertson and Wride, 1998) [5]. Следовательно, фиксация быстрого возрастания значений I_c свыше 2,6 будет свидетельствовать о возможном переходе зонда из глинистых грунтов в песчаные грунты, и соответственно, при уменьшении этого критического значения ниже 2,6 можно уверенно предполагать обратный переход из глинистых грунтов в песчаные.

Обсуждение вопросов идентификации грунтов в ходе статического зондирования может опираться на две типовые модели взаимодействия зонда и окружающих пород.

В грубозернистых несвязных грунтах (от песков до галечников) такое взаимодействие происходит в рамках дренированного состояния рабочей зоны. Было показано (Schneider et al., 2004), что в песках процесс взаимодействия с конусом определяется числом и площадью контактов, что, в свою очередь, зависит от таких факторов, как относительная плотность, действующие эффективные напряжения, переориентировка зёрен в ходе естественных процессов литификации [8]. Эти же факторы определяют скорости поперечных сейсмических волн V_s, что позволяет использовать геофизические модели грунтовых сред для корреляции с результатами зондирования с дальнейшим выходом на связи между V_s, чистым сопротивлением конусу и модулем сдвига G₀ для различных типов песчано-глинистых грунтов. Проверка этих зависимостей продолжается уже более 20 лет на основе применения сейсмозондов в различных геологических условиях. Важно подчеркнуть, что названные зависимости доказывают наличие прямой связи между результатами зондирования и деформационными характеристиками грунтов, прежде всего, модулем деформации.

Связь между скоростями поперечных волн и параметрами зондирования может быть также представлена в рамках уже упомянутых графоаналитических моделей SBT_n (рис. 1).

 

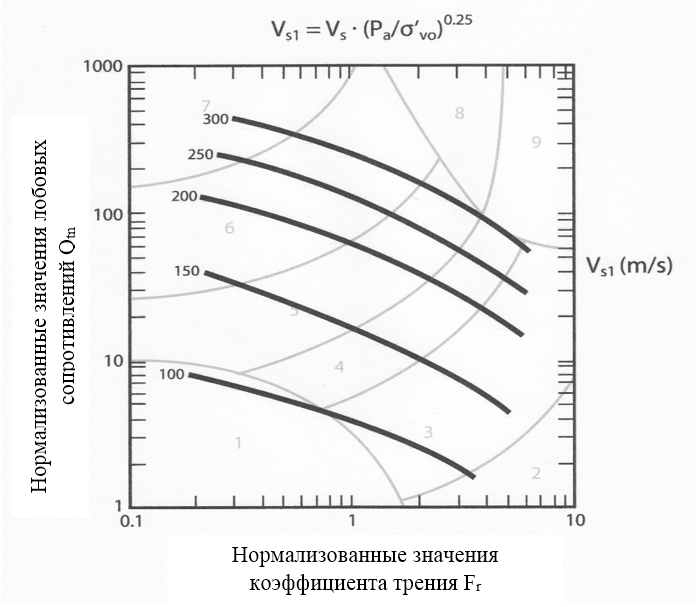
Рис. 1. Классификационная зональная диаграмма связи нормализованных значений скоростей поперечных волн V_s1 и типовых моделей грунтов координатах Q_tn и F_r [7]

 

Указанная взаимосвязь была проверена на большом фактическом материале (более 1000 пар соответствующих значений), при этом разброс значений был весьма значительный:

Q_tn от 0,67 до 577 (среднее 59);

F_r от 0,15 до 13,13% (среднее 3,13);

V_s1 от 72 до 906 м/с (среднее 260);

σ’_v0 от 19 до 518 кПа (среднее 190).

Такой разброс определялся, прежде всего, степенью литификации изученных осадков, формирование которых охватывает значительный период геологической истории изученных отложений от голоцена до плейстоцена. В частности, в большинстве случаев молодые голоценовые образования характеризовались скоростями V_s1 менее 250 м/с. На диаграмме, приведённой на рисунке 1, такие результаты концентрированы в левом нижнем углу графика, в то время как скорости для плейстоценовых осадков тяготели к правому верхнему углу графика. Определенное влияние на разброс оказывала несогласованность в производстве замеров, когда результаты зондирования фиксируются через 2–5 см, а замеры сейсмических скоростей производятся через 1–1,5 м. Кроме того, возможны ошибки в определении возраста осадков [7].

Внутри полей, ограниченных критическими линиями состояния грунтов (critical state line – CSL) на рисунке 1, вычисление частных значений возможно на основе обобщённых зависимостей:

(6) или (6а)

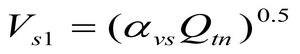
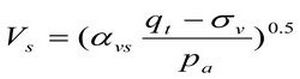
Соответственно, коэффициент α_vs = 10^{(0.55 Ic +1.68)}, (м/с)².

Следует подчеркнуть, что обсуждаемые зависимости требуют дополнительной проверки для различных типов грунтов. Можно предположить наличие общего тренда в распределении скоростей поперечных волн в отложениях разного возраста: чем старше и более литифицирован осадок, тем выше значение скорости V_s. Отметим, что в большинстве случаев при производстве рядовых изысканий проблемы геологической истории осадков решаются весьма приблизительно и привязка к региональной стратиграфии здесь просто необходима.

Вышеприведённые соображения показывают очевидную связь инженерной сейсмики и статического зондирования в составе инженерных изысканий.

Общеизвестна зависимость модуля сдвига G₀ от скорости поперечных волн V_s:

(7), где

— плотность грунта.

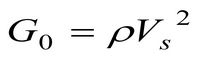
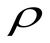
Отметим, что широкими возможностями определения важнейших геотехнических констант обладают современные методы сейсмической томографии, позволяющие не только вычислять такие параметры как модуль сдвига G₀, коэффициент Пуассона н, модуль упругости E’, модуль объёмной деформации B, но и наглядно отображать пространственную неоднородность инженерно-геологической структуры массива [9, 10, 11].

При низком уровне касательных напряжений и малых деформациях сдвига модуль сдвига может рассматриваться как константа, имеющая максимальное значение. В то же время была установлена связь модуля сдвига с нормализованными значениями действующих напряжений и чистым сопротивлением конусу:

(8)

(9), где

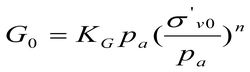
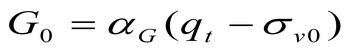
показатель n для грубозернистых грунтов варьирует около значения 0,5 [7].

Эмпирические коэффициенты K_G и α_G связаны между собой отношением:

(10)

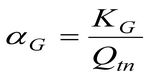
Исследования, предпринимаемые с 70-ых годов прошлого века и до настоящего времени, позволили предложить графическое отображение обсуждаемых зависимостей, при этом они были распространены не только на песчаные, но и на глинистые грунты в широком диапазоне, как в отношении геологического возраста, так и степени уплотнения и цементации (рис. 2):

 

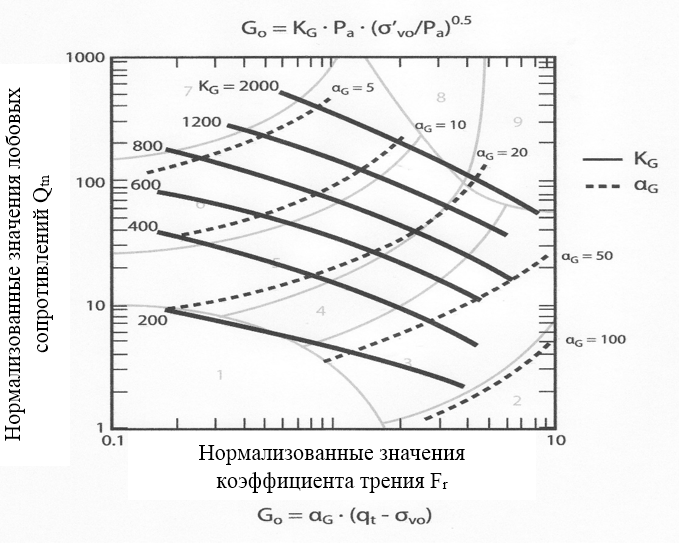
Рис. 2. Диаграмма связи коэффициентов K_G и α_G и нормализованных моделей грунтов [7]

 

В конечном счёте, модуль сдвига для молодых рыхлых осадков может быть вычислен по формуле:

(11)

Следует отметить, что указанная зависимость, равно как и графики, представленные на рисунках 1 и 2, менее надёжны для глинистых грунтов, когда типологический индекс грунта I_c>2,6. Наиболее достоверны они для кварцево-полевошпатовых песков четвертичного возраста (от плейстоцена до голоцена), когда I_c <2,6.

Очень существенным достижением в области приложения результатов зондирования к оценке деформационных свойств грунтов является установленная зависимость между модулем упругости E’ и чистым сопротивлением конусу (q_t – σ_v0), подтверждённая на большом массиве данных по несцементированным силикатным пескам четвертичного возраста, когда I_c <2,6 [7]:(12)

, (12)

 

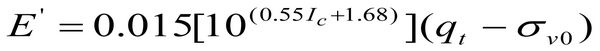
Из приведённых зависимостей видно, что модуль упругости и модуль сдвига связаны приблизительным отношением E'~ 0,8G₀.

Если необходимо поднять надёжность определения модуля Е' и соответственно снизить риск недостоверной интерпретации результатов зондирования, следует в каждом конкретном случае в указанную формулу вводить значения степени нагрузки q/q_ult, где q – приложенная к массиву нагрузка (чистое давление на основание от веса сооружения), а q_ult – предельная нагрузка (расчётное сопротивление несущего слоя), т.е.

(13),

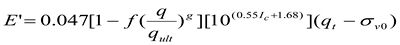
при этом для несцементированных грунтов предполагается равенство эмпирических констант, отражающих историю формирования напряжённого состояния грунтов в массиве, соответственно f = 1, g = 0,3 (Fahey and Carter, 1993; Mayne, 2005) [12,13]. Графоаналитическая связь модуля Е’ с нормализованными моделями грунтов SBT_n может быть также закреплена в виде диаграммы:

 

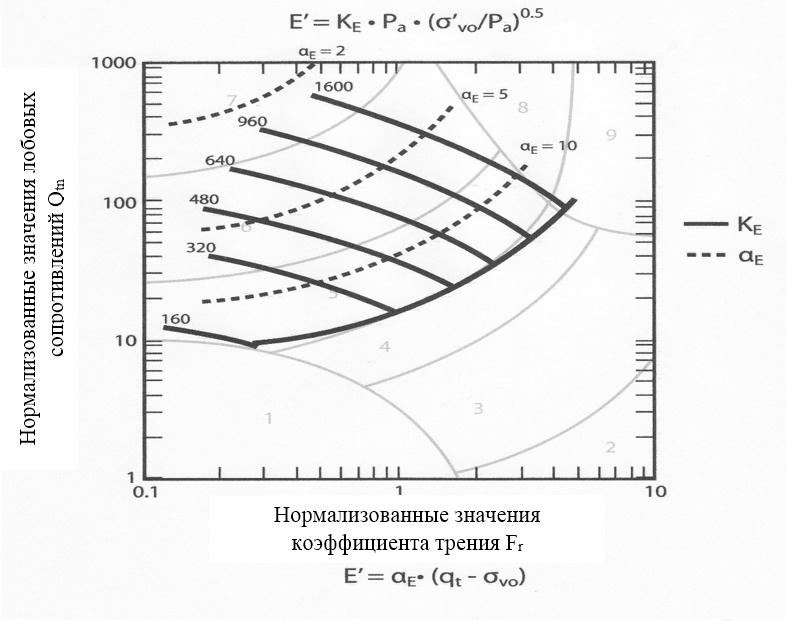
Рис. 3. Диаграмма связи модуля Е’ через коэффициенты K_E и α_E с нормализованными моделями грунтов [7]

 

Модуль деформации, определённый по указанной зависимости для песчаных грунтов различной степени уплотнения и цементации, многократно использовался для предсказания осадки под различными нагрузками, при этом сходимость с результатами опытных нагрузок на штампы больших размеров характеризовалась весьма большим разбросом [7]. Точность и достоверность таких предсказаний во многом зависит от натурных замеров сейсмических скоростей при производстве зондирования, которые позволяют откорректировать модуль деформации. Анализ приводимых результатов показывает, что большое значение имеет однородность строения геологического разреза и обоснованность его усреднения в рамках нормализованных моделей, о которых говорилось выше. С самого начала серьёзных исследований в области статического зондирования неоднократно доказывалась важность учёта литологических характеристик и напряжённого состояния грунтов в массиве (Robertson and Campanella, 1983, 1989; Kulhawy and Mayne, 1990; Jefferies and Been, 2006) в их естественном ненарушенном залегании [2,14,15,16] при интерпретации результатов и выходе на нормализованные модели грунтов. Например, для песков, представляющих наиболее простые модели, следует учитывать такие характеристики как минеральный состав, степень окатанности зёрен, относительную плотность сложения и их потенциальную сжимаемость. Очень часто в этом отношении наблюдается существенные расхождения между оценками по традиционным лабораторным данным и натурным наблюдениям. Именно здесь заложены высокие риски получения ошибочных выводов и ошибочной интерпретации результатов зондирования, которые затем могут перейти в область числового решения различных геотехнических задач.

Ещё более сложные проблемы возникают при первоначальной оценке состояния глинистых чувствительных грунтов, в которых при зондировании развивается высокое избыточное поровое давление и коэффициент порового давления B_q>1. На основе исследований в калибровочной камере Джефри и Бина в 2006 году (Jefferies and Been, 2006) и последующих наблюдений Шаттла и Каннинга (Shuttle and Cunning, 2007), а также натурных измерений Райда с соавтрами (Wride at al., 2000), Робертсон предлагает использовать комплексный параметр состояния (ψ), который в случае глинистых грунтов (I_c>2,6) должен дополняться оценками коэффициента переуплотнения (OCR) [4,7]. Этот коэффициент, зависящий, прежде всего, от напряжённого состояния и пластической жёсткости, может использоваться для широкого спектра песчано-глинистых осадков, когда точное представление о модели грунта затруднено.  (14),

, (14)

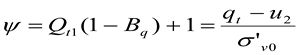
при этом в общем случае коэффициент переуплотнения КПУ (англ., OCR) представляет отношение максимальных эффективных напряжений, испытанных грунтом в прошлом σ'_p, к существующим эффективным напряжениям, определяемым нагрузкой от перекрывающих слоёв, σ’_v0 и природным поровым давлением u₀. (15)

, (15)

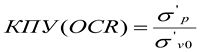
Связь между параметром состояния ψ и нормализованными моделями грунтов может быть закреплена графически (рис. 4):

 

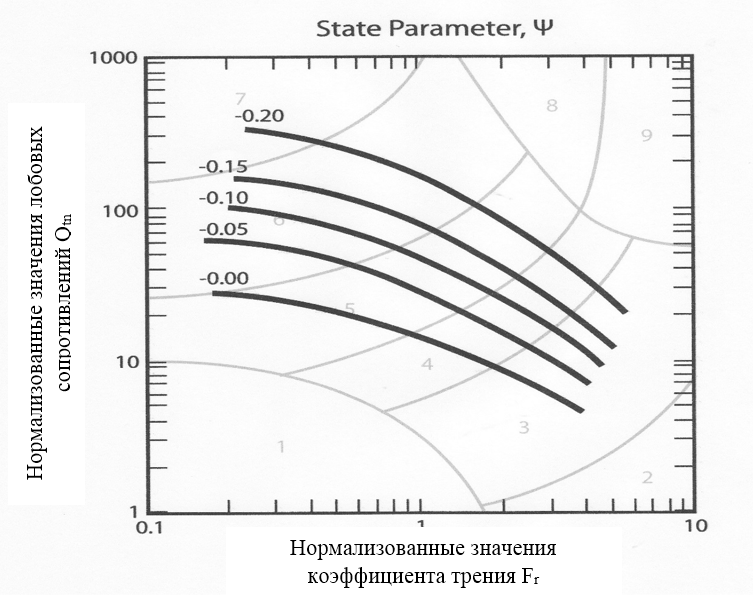
Рис. 4. Диаграмма связи комплексного параметра состояния ψ с нормализованными моделями грунтов [7]

 

Работы Робертсона и Кампанеллы (Robertson and Campanella, 1983), развитые затем капитальными исследованиями Кульхейви и Мейна (Kulhawy and Mayne, 2006) [15,16,17] в области дилатансии песков, позволяют связать пиковые значения угла внутреннего трения песчаных грунтов с нормализованными моделями грунтов в рамках базовой диаграммы состояний в диапазоне значений типологического индекса грунтов I_c от 1,8 до 2,2.

 

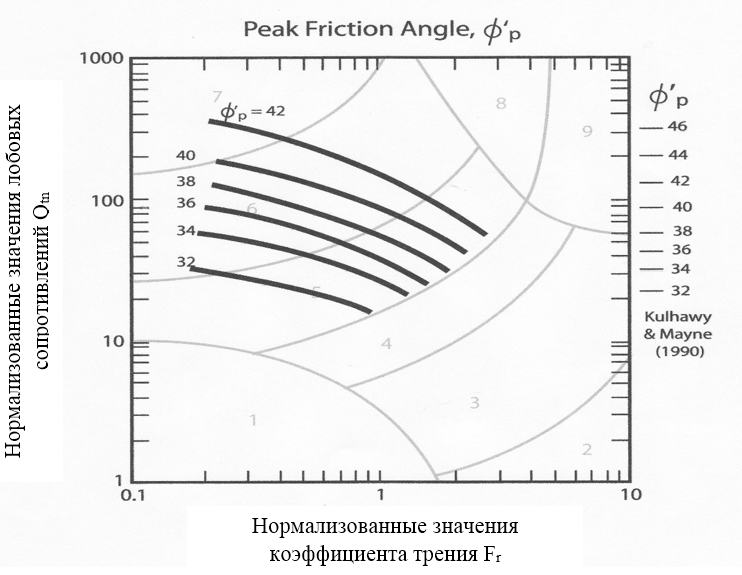
Рис. 5. Диаграмма связи пиковых значений угла внутреннего трения песков с нормализованными моделями грунтов

 

На приведённом графике видно, что, когда нормализованный коэффициент трения F_r возрастает (соответственно возрастает сжимаемость грунта), нормализованные значения лобовых сопротивлений уменьшаются при постоянном значении угла трения. Это согласуется с фактами наблюдений, когда высокие значения угла трения  φ’_p в сильно сжимающихся карбонатных песках соответствуют небольшим значениям лобовых сопротивлений. В области высоких значений φ_p на указанную зависимость может оказывать дополнительное влияние эффект цементации.

Интерпретация результатов зондирования в тонкозернистых грунтах должна базироваться на представлениях о недренированных условиях работы зонда, соответственно чему для типовой модели грунта используется нормализованное значение лобовых сопротивлений Q_t1 (n=1). Однако надо иметь в виду, что в области высокоглинистых грунтов (I_c>2,6) более точны нормализованные модели при n > 1.

Как было отмечено выше, оценка состояния тонкозернистых грунтов и соответственно выход на их типовые модели требуют тщательного палеофациального анализа через определение коэффициента переуплотнения КПУ (OCR). Для вычисления данного показателя (см. ф. 15) необходимо знать историю литификации грунта и особенно роль цементации в процессе формирования структурных связей. Для грунтов, которые достигли определённой степени литификации, коэффициент переуплотнения представляет собой отношение напряжения на пределе текучести (максимальное напряжение, определяющее пластическое течение) к действующему эффективному напряжению, вызванному весом перекрывающих слоёв, при этом следует учитывать направление действия и тип нагрузки. По предложению Кулхейви и Мейна (Kulhawy and Mayne, 1990) генетически предопределённый предел напряжения текучести σ’_р можно определить по формуле [15]:

(16), где

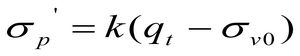
k = 0,33 (усреднённое значение для диапазона 0,2…0,5). Для сильно переуплотнённых глин рекомендуется принимать k = 0,5.

Соответственно по результатам зондирования коэффициент переуплотнения может быть вычислен по следующей формуле:

(17)

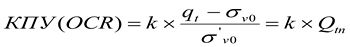
Для тонкозернистых глинистых грунтов установлено, что нормализованные значения сопротивления конусу Q_tn и коэффициента трения F_r определяются не только степенью консолидации, устанавливаемой по коэффициенту переуплотнения КПУ (OCR), но и чувствительностью грунта St. Эта зависимость была исследована на основе установленной прямой связи боковых сопротивлений при зондировании со значениями недренированного сопротивления прямому сдвигу для перемятых глинистых грунтов. В высокочувствительных грунтах даже незначительные нарушения естественного сложения приводят к изменению показаний муфты трения, которые хорошо коррелируют со значениями сопротивления недренированному прямому сдвигу (Lunne at al., 1997) [4].

Для нормально консолидированных (NC) глинистых осадков коэффициент чистого прямого среза в недренированных условиях изменяется в пределах 0,2…0,3 при среднем значении 0,22 [7]:

(18)

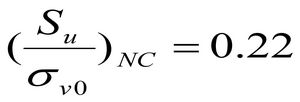
Максимальные значения указанного коэффициента определяются из выражения:

, (19), где

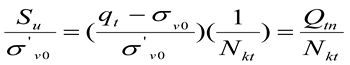
N_kt – фактор конуса, варьирующий в интервале 10…20 (среднее значение 14). При указанном среднем значении N_kt = 14 коэффициент прямого среза в недренированных условиях будет определяться по формуле:

, (20)

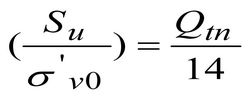
Из допущения связи боковых сопротивлений и сопротивления перемятого грунта прямому срезу в недренированных условиях (Su (remolded) = fs) следует вывод о том, что приведённые значения указанного коэффициента могут быть определены из выражения:

,  (21)

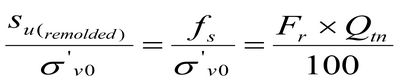
Из деления уравнений (20) на (21) получаем общее выражение для показателя чувствительности тонкозернистых глинистых грунтов:

,  (22)

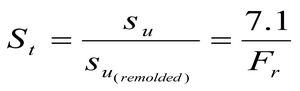
Взаимосвязи оценок состояния грунта через КПУ (OCR) и S_t в пределах нормализованных моделей для тонкозернистых глинистых грунтов (см. области 1,2,3 и 4 на основной диаграмме SBT) были рассмотрены при диапазонах изменения S_t = 1…10 и OCR = 1…25, при этом коэффициент прямого среза в недренированных условиях (см. формулу 18) охватывал широкую область значений от 0,022 до 2,89. Значение указанного коэффициента 0,22 фактически фиксирует нормально уплотненные грунты. Отталкиваясь от этого значения, можно оценивать различные состояния глинистых грунтов, как в направлении увеличения их чувствительности, так и степени уплотнения (рис. 6). Отметим, что вся цепочка рассуждений по данному вопросу связана с надёжными замерами боковых сопротивлений по муфте трения при производстве зондирования и доказанным равенством su (remolded) = fs.

 

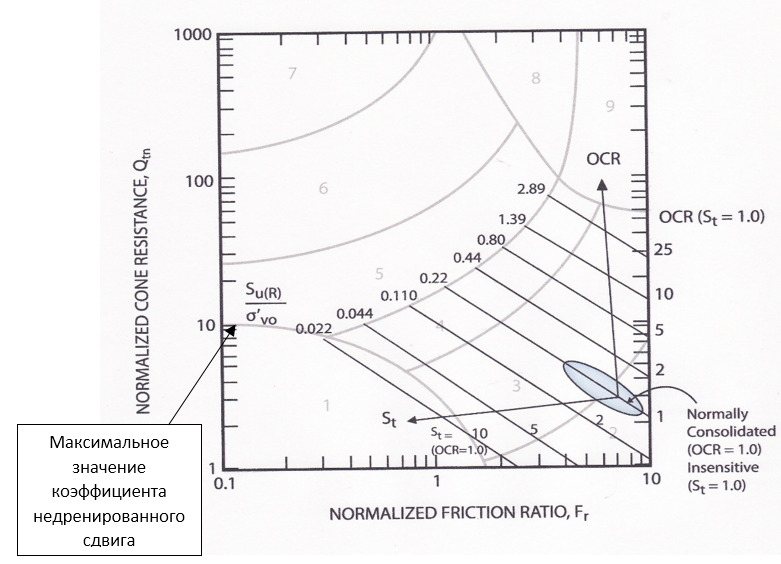
Рис. 6. Диаграмма, иллюстрирующая связь показателей состояния грунта (коэффициента переуплотнения КПУ (OCR) и коэффициента чувствительности S_t) с нормализованными моделями грунтов [7]

 

На приведённой диаграмме отчётливо видно, как меняются нормализованные параметры зондирования Q_tn и F_r в зависимости от чувствительности нормально консолидированных тонкозернистых грунтов (вдоль критической линии CSL со значением 0,22): с ростом показателя чувствительности St происходит незначительное уменьшение нормализованных значений лобовых сопротивлений Q_t1 в интервале 2…6 (среднее 3,08) (такую же тенденцию демонстрирует и коэффициент конуса N_kt в зависимости от действующих эффективных напряжений). При этом коэффициент трения в меньшей степени зависит от степени литификации и уплотнения, но в большей степени зависит от чувствительности грунта (см. формулу 22). Для сверхчувствительных глин (S_t >10) сопротивления боковому трению (соответственно и коэффициент трения F_r) могут быть очень низкими, при этом падает и точность определения данного показателя. Таким образом, наши представления о высокой чувствительности глинистых грунтов по результатам зондирования должны рассматриваться с большой осторожностью, т. е. необходима проверка этого показателя другими методами, например, с помощью вращательного среза крыльчаткой.

Из затронутых выше проблем исследования свойств тонкозернистых глинистых грунтов с очевидностью вытекает, что решение этих проблем требует применения полевых и лабораторных методов высокой разрешающей способности, при этом статическое зондирование, как один из таких методов, в значительной степени позволяет расширить границы комплексного анализа, обосновать надёжную корреляцию результатов полевых и лабораторных исследований и соответственно снизить уровень ошибочных интерпретаций. При интерпретации результатов зондирования в полной мере должны быть задействованы достоверные представления о чувствительности грунтов S_t, о степени их природного уплотнения или переуплотнения (КПУ или OCR), об эффективных напряжениях, значения которых определяют реакцию зонда при прохождении им грунтов различного состава и свойств.

В энциклопедической монографии, посвящённой статическому зондированию (Lunne et al., 1997) [4], была всесторонне исследована связь компрессионного модуля деформации и чистого сопротивления конусу в рамках эмпирической корреляции через коэффициент α_M:

(23), где

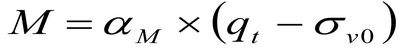
коэффициент α_M в тонкозернистых и органоминеральных грунтах широко варьирует в зависимости от пластичности и влажности.

Профессор Робертсон на основе своих исследований предлагает упрощённую корреляцию между компрессионным сжатием и нормализованными значениями лобовых сопротивлений:

при I_c >2,2

α_M = Q_tn, когда Q_tn < 14

α_M = 14, когда Q_tn >14

При I_c <2,2 (24)

В отличие от наблюдений Мейна, который полагал, что α_M изменяется в интервале от 1 до 10) (Mayne, 2007), Робертсон расширяет границы возможных изменений α_M от 2 до 14, когда Q_tn < 14 [7]. Предлагаемые зависимости подтверждаются многочисленными наблюдениями за параллельными определениями модуля компрессионного сжатия по лабораторным данным и по результатам зондирования (рис. 7).

 

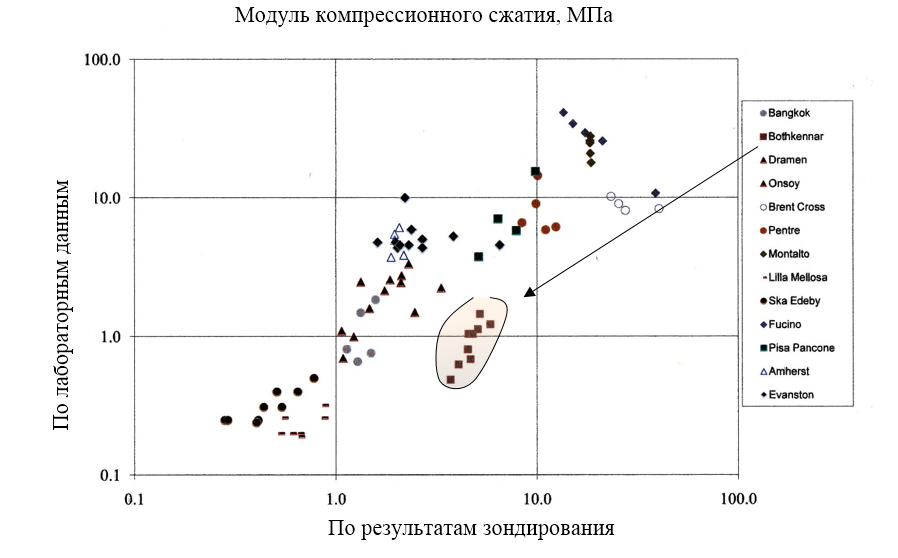
Рис. 7. Сравнение определений модуля компрессионного сжатия по лабораторным данным и по результатам зондирования на 12 объектах

 

В большинстве случаев модули деформации, полученные по лабораторным компрессионным испытаниям, проверялись обратным расчётом на основе наблюдений за осадками для реальных сооружений [7]. В целом, совпадение результатов сравнения (см. рис. 7) достаточно убедительны, чтобы рекомендовать указанные выше зависимости (см. формулы 23-24) для оценки модуля деформации при компрессионном сжатии в пылевато-глинистых грунтах, когда преобладают вертикальные перемещения. При этом снимаются проблемы отбора образцов чувствительных грунтов, когда малейшие нарушения природного сложения оказываются решающими для достоверной оценки деформируемости грунтов. Конечно, в нормально консолидированных грунтах использование результатов зондирования для определения модуля деформации наиболее оправдано по сравнению с высокочувствительными глинистыми грунтами, где необходимо учитывать такие свойства как пластичность, влажность, содержание органики. Как указывает проф. Робертсон, именно эти факторы определили наибольшие отклонения от общей зависимости для объекта «Bothkennar» в Англии (см. рис. 7).

Таким образом, рассмотренные выше расширенные возможности статического зондирования выстраиваются в последовательную методику интерпретации результатов при условии замеров порового давления и соблюдения единообразной методики выполнения всех процедур зондирования на базе IRTP, 1989, 1997. Указанная методика может быть реализована в любой компьютерной программе электронных таблиц, например Excel, где можно свести воедино ряд последовательных вычислений на основе обработки первичных цифровых файлов [18, 19]. При этом предполагается, что на площадках, где производится статическое зондирование, будет выполнено тщательное сопоставление с результатами бурения и будут создаваться опорные профили по точкам зондирования с расстоянием между пунктами зондирования не более 3 м [7].

Алгоритм углублённой обработки результатов статического зондирования должен включать в себя следующие процедуры.

• Перенос первичного цифрового файла с записью лобовых сопротивлений qc, боковых сопротивлений f_s и избыточного порового давления u₂ в электронную таблицу Excel.
• Корректировка параметров зондирования q_c и f_s (при необходимости соответственно предварительному расчленению разреза на песчаные и глинистые грунты.
• Расчёт вертикальных общих (σ_v0) и эффективных (σ' _v0) напряжений по всем точкам цифрового файла на основе детального опробования и лабораторных определений плотности и влажности грунтов.
• Принятие гипотезы о распределении по глубине природного фонового порового давления u₀ (если не было опытов по диссипации).
• Вычисление нормализованных значений Q_t1 и F_r (см. ф. 1,2).
• Вычисление фактора нормализации n для песчаных и глинистых слоёв разреза (см. ф. 3).
• Вычисление типологического индекса грунтов I_c по всем точкам цифрового файла при n=1 (см. ф. 5).
• Перенос данных на классификационную зональную диаграмму SBT_n (на диаграмму могут выноситься как все замеры, так и представляющие интервальные значения – средние, модальные, медианные).
• Поинтервальные определения скоростей поперечных сейсмических волн V_s (см. ф. 6 и 6а).
• Поинтервальные определения модуля сдвига G₀ и коэффициента Пуассона ν (см. ф. 8 – 11).
• Поинтервальные определения модуля E’ (см. ф. 13).
• Поинтервальные определения коэффициента переуплотнения КПУ (OCR) (см. ф. 17).
• Поинтервальные определения коэффициента чистого сдвига S_u/σ_v0 и коэффициента чувствительности S_t (см. ф. 18-21).
• Определение модуля общей деформации М (см. ф. 23-24).
• Построение графиков изменения вычисленных параметров по глубине.
• Расширенный коррелятивный анализ полученных показателей с результатами аналогичных определений показателей состава, состояния и свойств грунтов полевыми и лабораторными методами с привлечением данных, полученных в аналогичных инженерно-геологических условиях.

Все перечисленные интерпретационные процедуры были проверены на результатах статического зондирования в Северо-Западном регионе России и на территории Санкт-Петербурга [20], т. е. была произведена региональная привязка и проверка материалов зондирования для широкого спектра песчано-глинистых грунтов ледникового комплекса. Описанная процедура дополнялась применением рекомендованной проф. Робертсоном компьютерной программы GeoLogismiki, позволяющей в интерактивном режиме обрабатывать и анализировать результаты зондирования.

В третьей беседе о статическом зондировании автор предполагает обосновать общую классификацию грунтов по результатам СРТ, на конкретном примере рассмотреть характеристику и оценку грунтов, привести некоторые обобщённые характеристики грунтов по территории СПб, а также разобрать особенности применения СРТ для расчётов свайных оснований.

 

Список литературы

• Campanella, R. G., Gillespie, D. and Robertson, P. K., 1982. Pore pressures during cone penetration testing. In Proceedings of the 2-nd European Symposium on Penetration Testing, ESPOT II. Amsterdam. F.F. Balkema, pp. 507-512.
• Robertson, P.K. and Campanella R.G., 1989. “Desing Manual for Use of CPT and CPTU”, University of British Colambia, BC.
• Ahmadi, M.M. and Robertson P.K., 2005. Thin layer effects on the CPT qc measurement. Canadian Geotechnical Journal, 42 (9): 1302-1317.
• Lunne T., Robertson P.K., Powell J.J., 1997. Cone Penetration Testing in Geotechnical Practice. Blackie Academic & Professional.
• Robertson, P. K. and Wride, C.E., 1998. Evaluation cyclic liquefaction potential using the cone penetration test. Canadian Geotechnical Journal, Ottawa, 35 (3): 442-459.
• Zhang, Z., Robertson, P.K. and Brachman, R.W.I., 2002, Estimating Liquefaction induced Ground Settlements From CPT for Level Ground, Canadian Geotechnical Journal, 39 (5): 1168-1180.
• Robertson P. K., 2009. Interpretation of Cone Penetration Tests – a unified approach. MS 08-158. Submitted to the Canadien Geotechnical Journal.
• Schneider, JA, McGillivray, AV and Mayne, PW, 2004. Evaluation of CPTU intra correlation at sand sites in the Lower Mississippi River valley, USA, Geotechnical & Geophisical Site Characterization, vol. 1, (Proc. ISC-2, Porto), Millpress, Rotterdam, 1003-1010.
• Курилович И. А., Веселов В. Н., 2007. Использование высокоразрешающей сейсморазведки при решении инженерно-геологических задач, связанных с проблемами строительства и эксплуатации объектов и сооружений в городских агломерациях. Материалы международной геологической конференции, г. Казань, 13-16 ноября 2007 г., т. II, с.с. 298-302.
• Захаров М. С., Курилович И. А., Веселов В. Н., 2007. Инженерно-геологическая характеристика и оценка строительной площадки по материалам статического зондирования и высокочастотного сейсмического профилирования. В сб. Научно-практические проблемы геотехники. СПб ГАСУ, с.с. 242-254.
• Курилович И. А., Веселов В. Н., 2009. Возможность использования современных геофизических методов для исследования изменений свойств грунтов при техногенных воздействиях. Ж. Инженерные изыскания, №2, с. с. 54-56.
• Fahey, M. and Carter, J.P., 1993. A finite element study of the pressuremeter in sand using a nonlinear elastic model. Canadian Geotechnical Journal, 30 (2): 348-362.
• Mayne, P.W., 2005. Integrated Ground Behavior: In-Situ and Lab Tests, Deformation Characteristics of Geomaterials, vol. 2 (Proc. Lyon), Taylor & Francis, London, pp. 155-177.
• Jefferies, M. G. and Been, K., 2006. Soil Liquefaction – A critical state approach. Taylor & Francis, ISBN 0-419-16170-8.
• Kulhawy, F.H. and Mayne, P.H., 1990. Manual on estimating soil properties for foundation desing, Report EL-6800 Electric Power Research Institute, EPRI, August, 1990.
• Robertson, P. K. And Campanella, C.E., 1983. Interpretation of cone penetration tests – Part I (sand). Canadien Geotechnical Journal, 20 (4): 718-733.
• Robertson, P. K. and Campanella, C.E., 1983. Interpretation of cone penetration tests – Part II (clay). Canadien Geotechnical Journal, 20 (4): 734-745.
• Захаров М. С., 2008. Статическое зондирование в инженерных изысканиях. Учебное пособие. СПб ГАСУ.
• Захаров М. С., 2006. Модели поведения основных параметров статического зондирования в типовом геологическом разрезе Санкт-Петербурга. Вестник гражданских инженеров, №3(8), СПб ГАСУ.
• Захаров М. С., 2015. Статическое зондирование. Анализ и обобщение опыта работы в Северо-Западном регионе России. Lambert. Academic Publishing. 84 c.