Обзор работы Вермеера и Де Борста о неассоциированной пластичности грунтов и бетона. Часть 8

ПОДХОДЫ К РАЗРАБОТКЕ МОДЕЛЕЙ ПОВЕДЕНИЯ МАТЕРИАЛОВ ПРИ ЦИКЛИЧЕСКОМ НАГРУЖЕНИИ

С точки зрения Вермеера и Де Борста [8] разработка надежных конститутивных (определяющих) моделей поведения материалов при циклическом нагружении является очень сложной задачей. К моменту написания рассматриваемой работы [8] достаточно успешными ее авторам казались только модели, нацеленные на описание циклического поведения металлов, например: модель Бесселинга, описывающая поведение материала, составленного из различных элементов объема, испытывающих одинаковую общую деформацию, но имеющих различные пределы текучести (Besseling, 1958); модель Мроза (Mroz, 1967), включающая две вложенных одна в другую поверхности – начала текучести и полного перехода материала в пластическое состояние; модель комбинированной поверхности нагружения Дафалиаса (Dafalias, 1975), включающая поверхность текучести и предельную поверхность, положение которой определяет развитие нелинейных деформаций и разрушение материала.

Что касается дисперсных и сцементированных зернистых грунтов и бетона, то ко времени публикации работы [8] ситуация представлялась Вермееру и Де Борсту достаточно неопределенной. Были предприняты кое-какие попытки смоделировать циклическое поведение дисперсного грунта, используя инкрементные нелинейные модели (Chambon, Darve, 1984; Robinet, Mohkam, 1982 и др.). В таких моделях инкрементальная зависимость «напряжение – деформация» имела следующую форму (напомним, что набор буквенного обозначения жирным шрифтом означает столбцовую матрицу, а точка над ним – его материальную производную по времени, то есть скорость изменения):

вычислений. Кроме того, в них обычно требуется очень большое количество материальных констант (иногда более 20), что почти исключает их использование для практических инженерных целей.

Другим типом инкрементных нелинейных моделей является инкрементально-нелинейная эндохронная теория пластичности, первоначально предложенная Валанисом (Valanis, 1971) для описания реакций металлов и расширенная Базантом и Батом (Bazant, Bhat, 1976) для зернистых материалов. Однако, как считают Вермеер и Де Борст, применение моделей такого типа является довольно громоздким и в некоторых случаях гистерезисное поведение дисперсных и сцементированных зернистых материалов может быть описано только с помощью уж очень хитроумных приемов, например с использованием концепции скачкообразного кинематического упрочнения (Bazant, 1978).

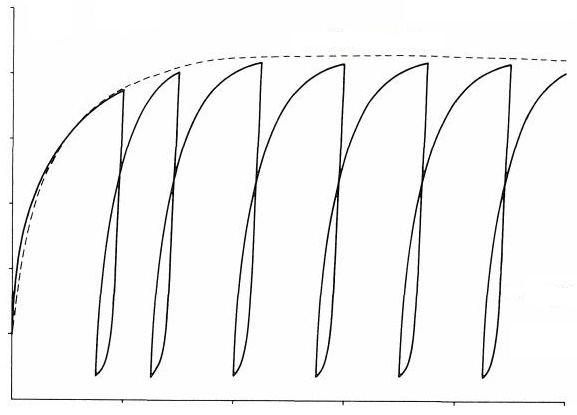
Еще один подход был предложен Базантом и Кимом (Bazant, Kim, 1979), которые объединили теорию нассоциированной пластичности с теорией трещинобразования Дугилла (Dougill, 1976), в которой для ограничения упругой области используется критерий, выражаемый в деформациях, а не в напряжениях. Кроме того, в отличие от теории пластичности в теории трещинобразования вместо использования упругой жесткости принимается, что разгрузка происходит вдоль секущей ветви (рис. 1).

К моменту написания рассматриваемой работы [8] теория трещинобразования, включая ее сочетание с теорией пластичности, не имела с точки зрения авторов большого практического значения, так как еще предстояло решить некоторые фундаментальные вопросы, в том числе для облегчения использования теории Дугилла в компьютерных программах. К тому же сочетание теорий пластичности и трещинобразования может иметь много комбинаций, не все из которых приводят к согласованным моделям.

Рис. 1. Теория Дж. Дугилла (Dougill, 1976) преувеличивает уменьшение модуля разгрузки – повторного нагружения

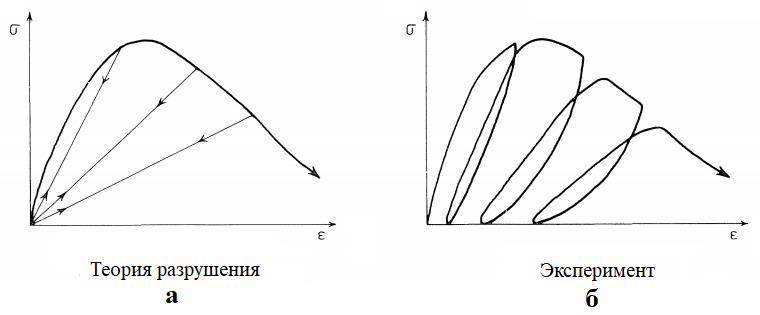
Результаты испытаний, как отмечают Вермеер и Де Борст, показывают, что сцементированные зернистые материалы вблизи пиковой прочности и после нее действительно показывают возрастающее ухудшение упругой жесткости из-за образования микротрещин, но это ухудшение сильно преувеличено в теории Дугилла (см. рис. 1). В принципе, оно может быть включено в теорию пластичности, причем вместо того, чтобы использовать постоянный модуль Юнга, его можно связать с пористостью материала, но не непосредственно, а через такой параметр пластической деформации, как эффективная деформация. При этом, подчеркивают авторы, и ухудшение упругой жесткости, и когезионное разупрочнение (см. часть 6 [6]) вызваны образованием микротрещин в сцементированных зернистых материалах, поэтому подходы к ним должны быть более или менее сходными.

Относительно выбора направления конститутивного моделирования циклического поведения дисперсных и сцементированных зернистых материалов к моменту написания рассматриваемой работы [8] не было единого мнения. По мнению ее авторов, лучше всего было следовать достаточно успешным идеям в области пластичности металлов. Например, Мроз (Mroz, 1978, 1979) и Дафалиас (Dafalias, 1979, 1982) адаптировали свои модели для предсказания поведения глин, а Моленкамп (Molenkamp, 1982) разработал кинематическую упрочняющуюся модель для песка на основе модели «вложенной» поверхности текучести Мроза. Также была предложена модель предельной (граничной) поверхности пластичности для описания поведения бетона при циклическом нагружении (Fardis et al., 1983), хотя ее недостатком было то, что она также являлась инкрементально-нелинейной (из-за того, что в ней принималось исчезновение упругой области).

Далее Вермеер и Де Борст излагают идеи Дафалиаса (Dafalias, 1979, 1982) с добавлением собственных выкладок, ближе соответствующих классическому подходу, и на этой основе, а также на основе идей, разработанных в предыдущих главах для монотонного нагружения, обсуждают возможности разработки гистерезисных моделей для дисперсных и сцементированных зернистых материалов. При этом авторы отмечают, что идеи Мроза, тесно связанные с идеями Дафалиаса, также могут использоваться в качестве отправной точки для разработки моделей, описывающих гистерезисное поведение песка и бетона.

ПОЛНЫЙ ТЕКСТ СТАТЬИ с рисунками, формулами и списком литературы читайте в формате pdf. СКАЧАТЬ